So führen sie einen tukey-kramer-post-hoc-test in excel durch
Eine einfaktorielle ANOVA wird verwendet, um zu bestimmen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr unabhängigen Gruppen besteht.
Die in einer ANOVA verwendeten Annahmen sind wie folgt:
Die Nullhypothese (H 0 ): µ 1 = µ 2 = µ 3 = … = µ k (die Mittelwerte sind für jede Gruppe gleich)
Die Alternativhypothese: (Ha): Mindestens eines der Mittel unterscheidet sich von den anderen
Wenn der p-Wert der ANOVA unter dem Signifikanzniveau liegt, können wir die Nullhypothese ablehnen und daraus schließen, dass wir über ausreichende Beweise verfügen, um zu sagen, dass sich mindestens einer der Gruppenmittelwerte von den anderen unterscheidet.
Dies sagt uns jedoch nicht, welche Gruppen sich voneinander unterscheiden. Dies zeigt uns einfach, dass nicht alle Gruppendurchschnitte gleich sind. Um genau zu wissen, welche Gruppen sich voneinander unterscheiden, müssen wir einen Post-hoc-Test durchführen.
Der am häufigsten verwendete Post-hoc-Test ist der Tukey-Kramer-Test , der den Mittelwert zwischen jeder paarweisen Kombination von Gruppen vergleicht.
Das folgende Beispiel zeigt, wie der Tukey-Kramer-Test in Excel durchgeführt wird.
Beispiel: Tukey-Kramer-Test in Excel
Angenommen, wir führen eine einfaktorielle ANOVA für drei Gruppen durch: A, B und C. Die Ergebnisse der einfaktoriellen ANOVA sind unten dargestellt:
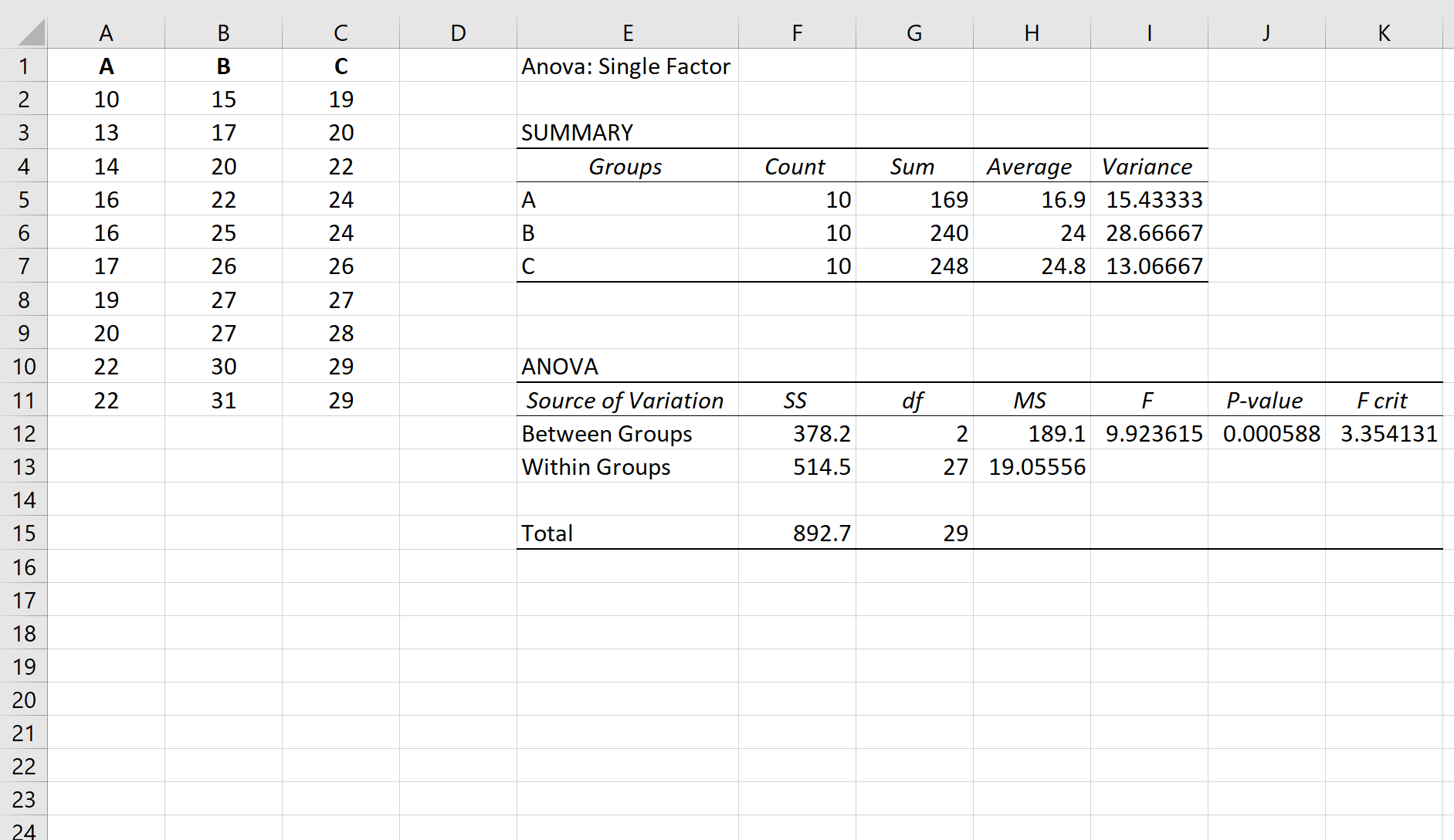
Verwandte Themen: So führen Sie eine einfaktorielle ANOVA in Excel durch
Der p-Wert der ANOVA-Tabelle beträgt 0,000588 . Da dieser p-Wert kleiner als 0,05 ist, können wir die Nullhypothese ablehnen und daraus schließen, dass die Mittelwerte zwischen den drei Gruppen nicht gleich sind.
Um genau zu bestimmen, welche Gruppenmittelwerte unterschiedlich sind, können wir einen Tukey-Kramer-Post-hoc-Test mit den folgenden Schritten durchführen:
Schritt 1: Ermitteln Sie den absoluten Mittelwertunterschied zwischen den einzelnen Gruppen.
Zunächst ermitteln wir die absolute Mittelwertdifferenz zwischen den einzelnen Gruppen mithilfe der in der ersten Tabelle des ANOVA-Ergebnisses aufgeführten Mittelwerte:
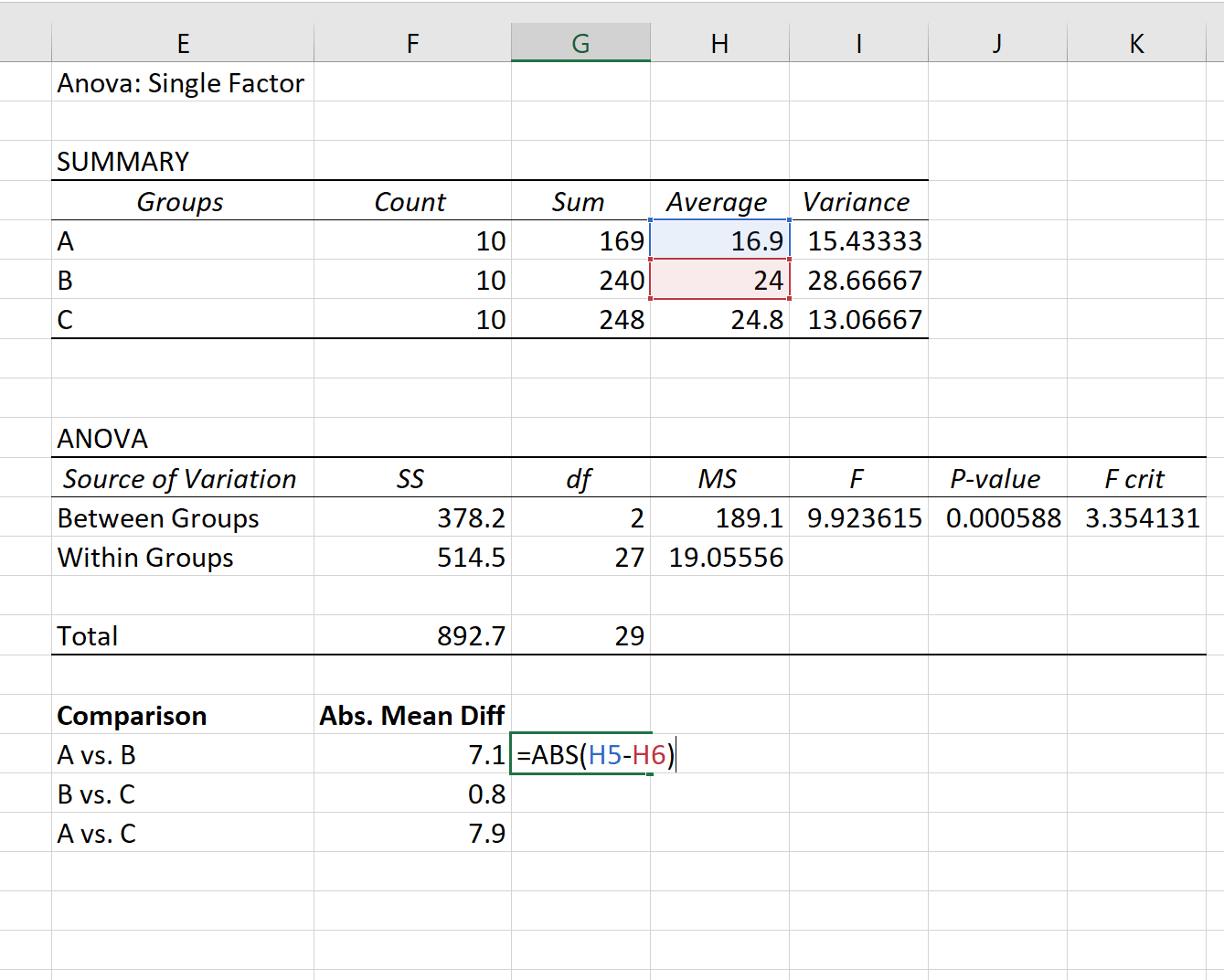
Schritt 2: Finden Sie den kritischen Wert von Q.
Als nächstes müssen wir den kritischen Wert von Q mithilfe der folgenden Formel ermitteln:
Kritischer Wert Q = Q*√(s 2 gruppiert / n.)
Gold:
- Q = Wert des Bereichs der Student-Tabelle Q
- s 2 gepoolt = Varianz gepoolt über alle Gruppen
- nicht. = Stichprobengröße für eine bestimmte Gruppe
Um den Q-Wert zu ermitteln, können Sie auf die Studentized Range Q-Tabelle zurückgreifen, die wie folgt aussieht:
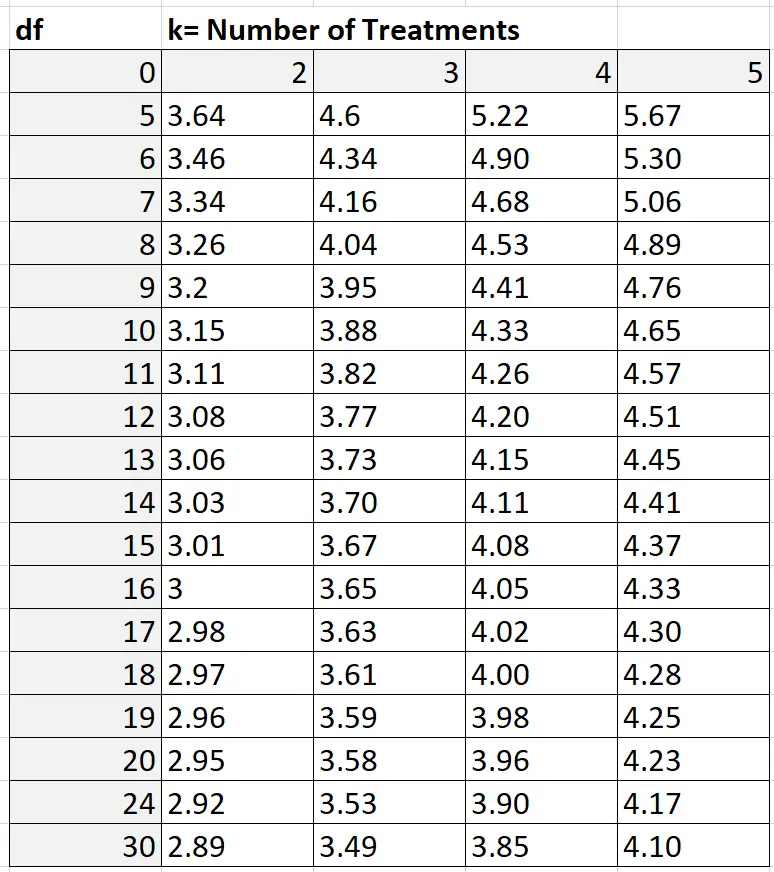
In unserem Beispiel ist k = die Anzahl der Gruppen, also k = 3. Die Freiheitsgrade werden wie folgt berechnet: nk = 30 – 3 = 27. Da 27 in der obigen Tabelle nicht aufgeführt ist, können wir eine konservative Schätzung von 24 verwenden . Basierend auf k = 3 und df = 24 finden wir, dass Q = 3,53 .
Die gepoolte Varianz kann als Durchschnitt der Varianzen der Gruppen berechnet werden, der sich als 19,056 ergibt.
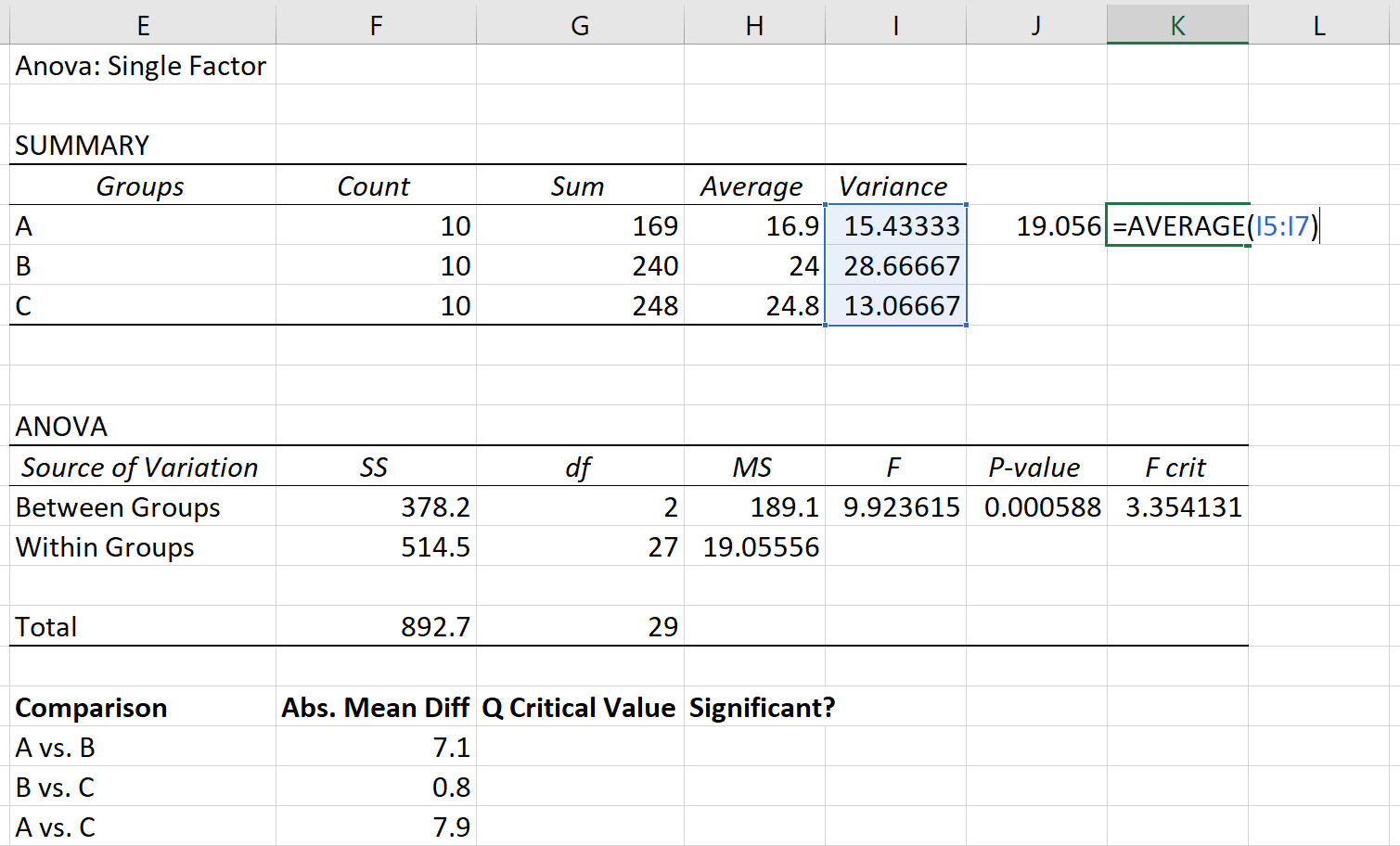
Schließlich beträgt die Stichprobengröße jeder Gruppe 10.
Somit kann unser kritischer Wert Q wie folgt berechnet werden:
Kritischer Wert Q = Q*√(s 2 gruppiert / n.) = 3,53*√(19,056/10) = 4,87 .
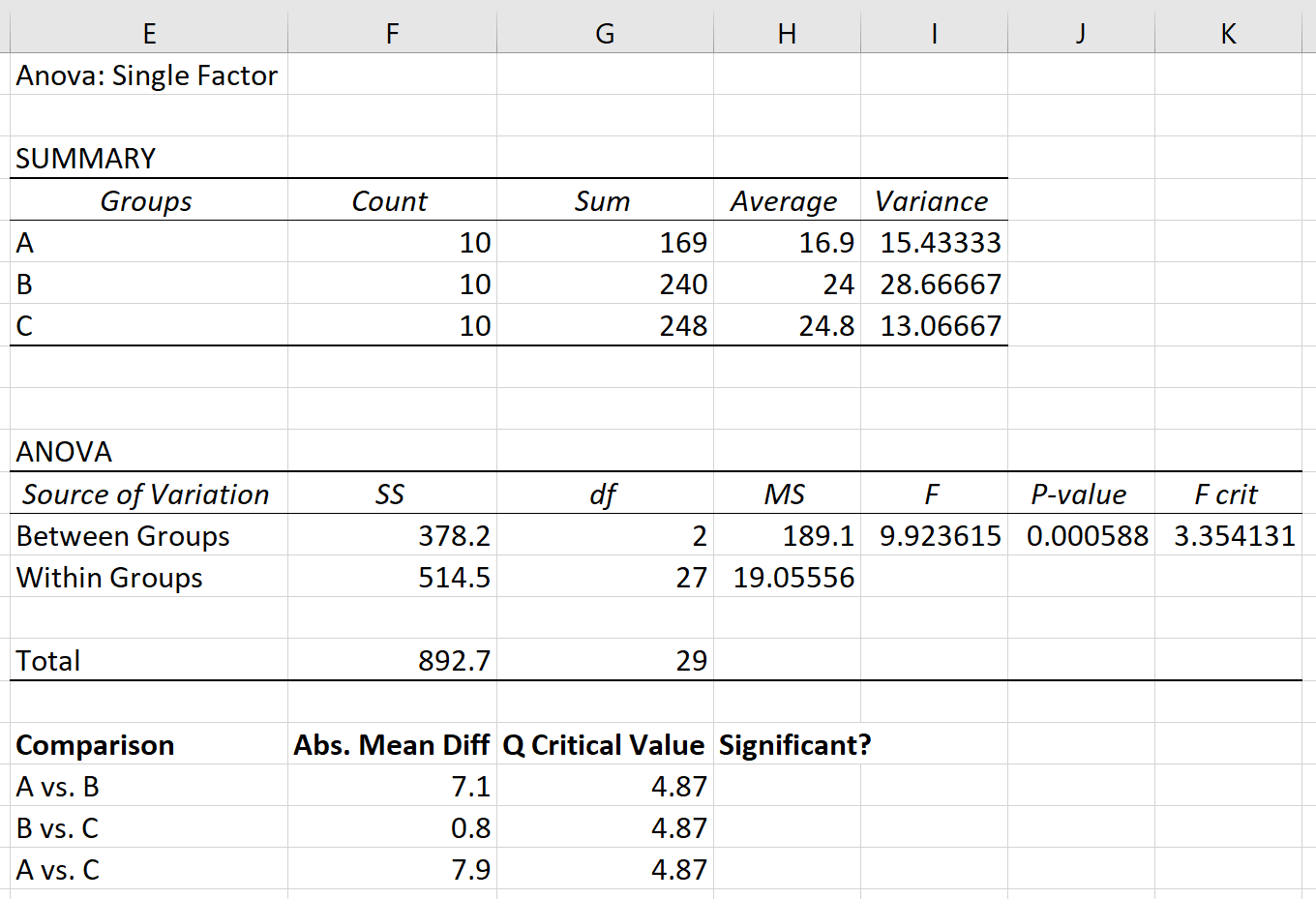
Schritt 3: Bestimmen Sie, welche Gruppenmittelwerte unterschiedlich sind .
Schließlich können wir die absolute Mittelwertdifferenz zwischen den einzelnen Gruppen mit dem kritischen Wert Q vergleichen. Wenn die absolute Mittelwertdifferenz größer als der kritische Wert Q ist, ist die Differenz zwischen den Gruppenmittelwerten statistisch signifikant:
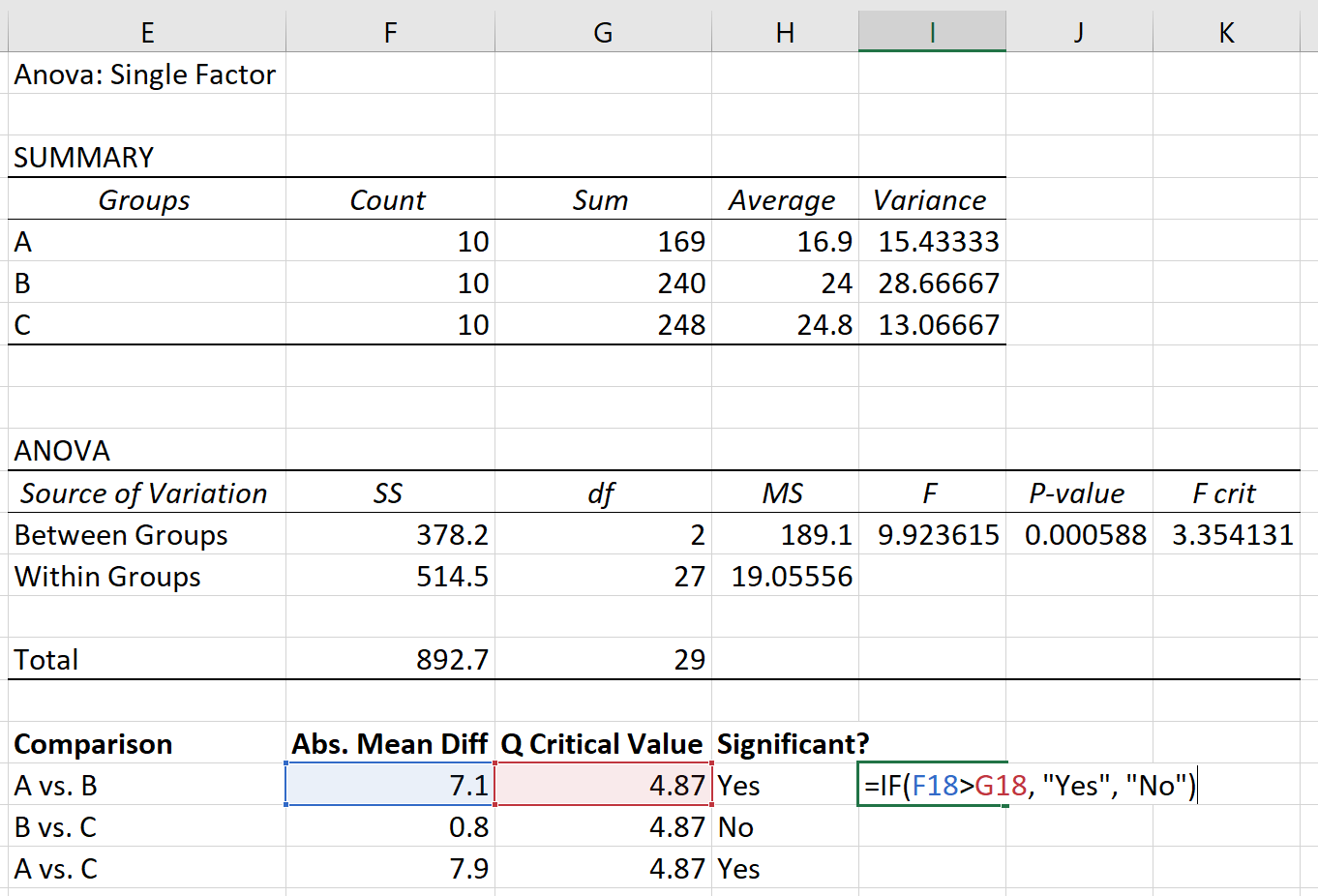
Basierend auf dem Post-hoc-Test von Tukey-Kramer haben wir Folgendes festgestellt:
- Der Mittelwertunterschied zwischen Gruppe A und Gruppe B ist statistisch signifikant.
- Der Mittelwertunterschied zwischen Gruppe B und Gruppe C ist statistisch nicht signifikant.
- Der Mittelwertunterschied zwischen Gruppe A und Gruppe C ist statistisch signifikant.
Zusätzliche Ressourcen
So führen Sie eine einfaktorielle ANOVA in Excel durch
Ein Leitfaden zur Verwendung von Post-Hoc-Tests mit ANOVA