So führen sie den tukey-test in r durch

Eine einfaktorielle ANOVA wird verwendet, um zu bestimmen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr unabhängigen Gruppen besteht.

Wenn der Gesamt -p-Wert der ANOVA-Tabelle unter einem bestimmten Signifikanzniveau liegt, verfügen wir über ausreichende Beweise dafür, dass sich mindestens einer der Gruppenmittelwerte von den anderen unterscheidet.

Dies sagt uns jedoch nicht, welche Gruppen sich voneinander unterscheiden. Dies zeigt uns einfach, dass nicht alle Gruppendurchschnitte gleich sind. Um genau zu wissen, welche Gruppen sich voneinander unterscheiden, müssen wir einenPost-hoc-Test durchführen.

Einer der am häufigsten verwendeten Post-hoc-Tests ist der Tukey-Test , der es uns ermöglicht, paarweise Vergleiche zwischen den Mittelwerten jeder Gruppe durchzuführen und gleichzeitig die Familienfehlerrate zu kontrollieren.

In diesem Tutorial wird erklärt, wie der Tukey-Test in R durchgeführt wird.

Hinweis: Wenn eine der Gruppen in Ihrer Studie als Kontrollgruppe gilt, sollten Sie stattdessen den Dunnett-Test als Post-hoc-Test verwenden.

Beispiel: Tukey-Test in R

Schritt 1: Passen Sie das ANOVA-Modell an.

Der folgende Code zeigt, wie man einen gefälschten Datensatz mit drei Gruppen (A, B und C) erstellt und ein einfaktorielles ANOVA-Modell an die Daten anpasst, um zu bestimmen, ob die Mittelwerte jeder Gruppe gleich sind:

 #make this example reproducible
set.seed(0)

#create data
data <- data.frame(group = rep (c("A", "B", "C"), each = 30),
                   values = c(runif(30, 0, 3),
                                   runif(30, 0, 5),
                                   runif(30, 1, 7)))

#view first six rows of data
head(data)

  group values
1 A 2.6900916
2 A 0.7965260
3 A 1.1163717
4 A 1.7185601
5 A 2.7246234
6 A 0.6050458

#fit one-way ANOVA model
model <- aov (values~group, data=data)

#view the model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)    
group 2 98.93 49.46 30.83 7.55e-11 ***
Residuals 87 139.57 1.60                     
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Wir können sehen, dass der Gesamt-p-Wert aus der ANOVA-Tabelle 7,55e-11 beträgt. Da diese Zahl weniger als 0,05 beträgt, haben wir genügend Beweise dafür, dass die Durchschnittswerte in jeder Gruppe nicht gleich sind. Wir können also den Tukey-Test durchführen, um genau zu bestimmen, welche Gruppenmittelwerte unterschiedlich sind.

Schritt 2: Führen Sie den Tukey-Test durch.

Der folgende Code zeigt, wie Sie die Funktion TukeyHSD() verwenden, um den Tukey-Test durchzuführen:

 #perform Tukey's Test
TukeyHSD(model, conf.level= .95 ) 

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = values ~ group, data = data)

$group
         diff lwr upr p adj
BA 0.9777414 0.1979466 1.757536 0.0100545
CA 2.5454024 1.7656076 3.325197 0.0000000
CB 1.5676610 0.7878662 2.347456 0.0000199

Der p-Wert gibt an, ob zwischen den einzelnen Programmen ein statistisch signifikanter Unterschied besteht oder nicht. Die Ergebnisse zeigen, dass es einen statistisch signifikanten Unterschied zwischen dem durchschnittlichen Gewichtsverlust jedes Programms auf dem Signifikanzniveau 0,05 gibt.

Besonders:

• P-Wert für die Mittelwertdifferenz zwischen B und A: 0,0100545
• P-Wert für die Mittelwertdifferenz zwischen C und A: 0,0000000
• P-Wert für die Mittelwertdifferenz zwischen C und B: 0,0000199

Schritt 3: Visualisieren Sie die Ergebnisse.

Wir können auch die Funktion plot(TukeyHSD()) verwenden, um Konfidenzintervalle zu visualisieren:

 #plot confidence intervals
plot(TukeyHSD(model, conf.level= .95 ), las = 2 )

Hinweis: Das Argument las gibt an, dass die Teilstrichbeschriftungen senkrecht (las=2) zur Achse stehen müssen.

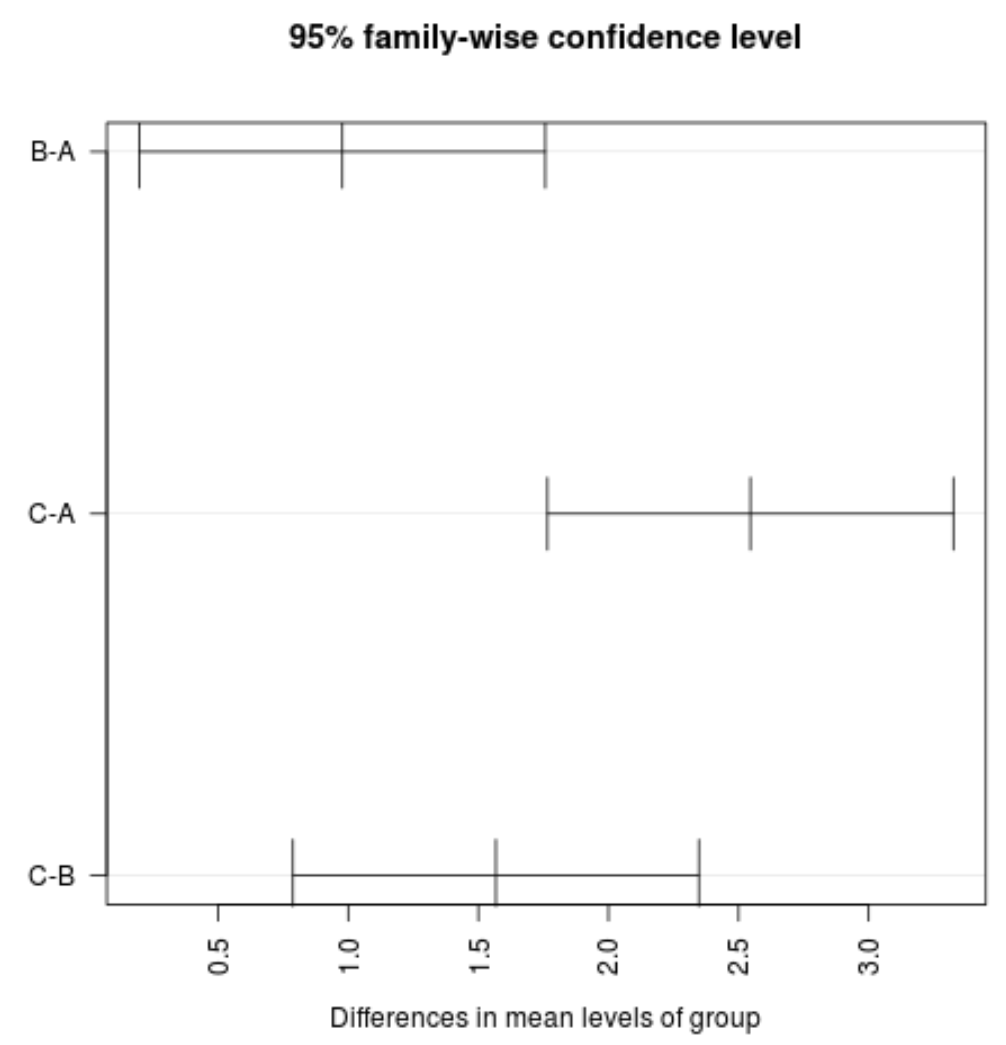
Wir können sehen, dass keines der Konfidenzintervalle für den Mittelwert zwischen den Gruppen den Wert Null enthält, was darauf hindeutet, dass es einen statistisch signifikanten Unterschied im mittleren Verlust zwischen den drei Gruppen gibt. Dies steht im Einklang damit, dass alle p-Werte für unsere Hypothesentests unter 0,05 liegen.

Für dieses spezielle Beispiel können wir Folgendes schlussfolgern:

• Die Mittelwerte der Gruppe C liegen deutlich über den Mittelwerten der Gruppen A und B.
• Die Mittelwerte der Gruppe B liegen deutlich über den Mittelwerten der Gruppe A.

Zusätzliche Ressourcen

Ein Leitfaden zur Verwendung von Post-Hoc-Tests mit ANOVA
So führen Sie eine einfaktorielle ANOVA in R durch
So führen Sie eine zweifaktorielle ANOVA in R durch