Tippen

Von Dr. Benjamin Anderson August 5, 2023 Statistiken Keine Kommentare

In diesem Artikel wird erläutert, was es bedeutet, eine Verteilung in der Statistik zu charakterisieren. So finden Sie die Definition der Typisierung, ein Beispiel für die Typisierung einer Variablen und können darüber hinaus anhand einer Schritt für Schritt gelösten Übung üben.

Was ist Tippen?

In der Statistik ist Normalisierung ein Prozess, bei dem eine lineare Transformation auf eine Verteilung angewendet wird, sodass ihr Mittelwert und ihre Standardabweichung gleich Null bzw. Eins sind.

Genauer gesagt besteht die Eingabe darin, den Mittelwert von der Zufallsvariablen zu subtrahieren und ihn dann durch die Standardabweichung zu dividieren.

Typisierung kann auch als Normalisierung oder Standardisierung bezeichnet werden.

Eingabeformel

Um eine Variable zu klassifizieren, müssen Sie ihren Mittelwert subtrahieren und ihn dann durch ihre Standardabweichung dividieren. Die Formel zur Eingabe einer Variablen lautet daher wie folgt:

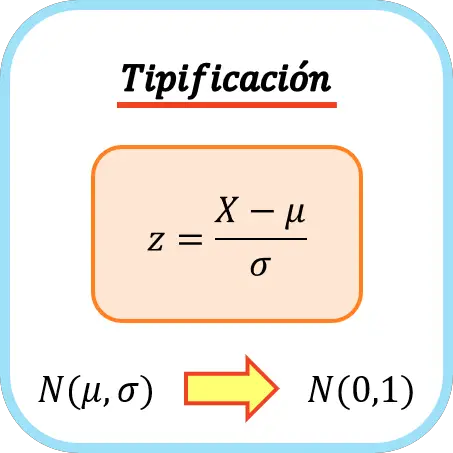
Gold

$\mu$

ist der Mittelwert der Variablen

$X$

Und

$\sigma$

seine Standardabweichung (oder Standardabweichung).

Daher handelt es sich bei der Eingabe tatsächlich um eine Variablenänderung, da eine lineare Transformation auf die Variable angewendet wird.

Beispieleintrag

Unter Berücksichtigung der Definition der Typisierung und ihrer Formel finden Sie im Folgenden ein konkretes Beispiel zum vollständigen Verständnis des Konzepts.

Eine kontinuierliche Zufallsvariable folgt einer Normalverteilung mit einem Mittelwert von 45 und einer Standardabweichung von 10. Wie groß ist die Wahrscheinlichkeit, einen Wert kleiner oder gleich 60 zu erhalten?

$N(45,10)$

Um die Wahrscheinlichkeit einer Normalverteilung zu ermitteln, müssen wir ihre charakteristische Tabelle verwenden. Dazu müssen wir jedoch zunächst den Typisierungsprozess durchführen. Also subtrahieren wir den Mittelwert und dividieren durch die Standardabweichung, um den Wahrscheinlichkeitswert zu erhalten:

$\displaystyle P(X\leq 60)=P\left(Z\leq\frac{60-45}{10}\right)=P(Z\leq 1,5)$

Sobald wir standardisiert haben, gehen wir zur Normalverteilungswahrscheinlichkeitstabelle über, um zu sehen, welcher Wahrscheinlichkeit der Wert 1,5 entspricht:

Wie in der Normalverteilungstypisierungstabelle zu sehen ist, entspricht der im vorherigen Schritt berechnete Wert der folgenden Wahrscheinlichkeit:

$\displaystyle P(Z\leq 1,5)=0,9332$

Die Wahrscheinlichkeit, einen Wert kleiner oder gleich 60 zu erhalten, liegt somit bei 93,32 %.

Tippübung gelöst

Berechnen Sie die folgenden Wahrscheinlichkeiten einer Normalverteilung, deren Mittelwert und Standardabweichung 120 bzw. 50 betragen.

$N(120,50)$

Die Wahrscheinlichkeit, einen Wert kleiner oder gleich 208 zu erhalten.
Die Wahrscheinlichkeit, einen Wert größer als 137 zu erhalten.

Sehen Sie sich die Lösung an

In beiden Abschnitten des Problems müssen wir die Normalverteilung eingeben, um die Wahrscheinlichkeiten zu berechnen.

Wir beginnen mit der Berechnung der Wahrscheinlichkeitstypisierung eines Werts, der kleiner oder gleich 208 ist:

$\displaystyle P(X\leq 208)=P\left(Z\leq\frac{208-120}{50}\right)=P(Z\leq 1,76)$

Schauen wir uns nun die obige Tabelle an, mit welcher Wahrscheinlichkeit der Wert 1,76 entspricht:

$\displaystyle P(Z\leq 1,76)=0,9608$

Zweitens berechnen wir die Wahrscheinlichkeit, einen Wert größer als 137 zu erhalten. Auf die gleiche Weise beginnen wir mit der Eingabe der Variablen:

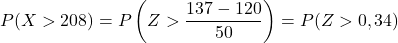$\displaystyle P(X> 208)=P\left(Z>\frac{137-120}{50}\right)=P(Z>0,34)“ title=“Rendered by QuickLaTeX.com“ height=“43″ width=“398″ style=“vertical-align: -17px;“> <p class=$ Die beigefügte Tabelle weist jedoch nur die niedrigsten kumulativen Wahrscheinlichkeiten auf. Um die Tabelle verwenden zu können, müssen wir daher zunächst die Wahrscheinlichkeit transformieren:

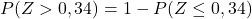$\displaystyle P(Z>0,34)=1-P(Z\leq 0,34)“ title=“Rendered by QuickLaTeX.com“ height=“19″ width=“252″ style=“vertical-align: -5px;“> <p class=$ Und schließlich werden wir der beigefügten Tabelle die Wahrscheinlichkeit entnehmen, die dem berechneten Wert von Z entspricht:

$\displaystyle P(Z>0,34)=1-P(Z\leq 0,34)=1-0,6331=0,3669″ title=“Rendered by QuickLaTeX.com“ height=“19″ width=“435″ style=“vertical-align: -5px;“> <div class=$

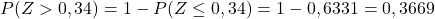
Welchen Sinn hat das Tippen?

Um die Bedeutung der Typisierung vollständig zu verstehen, sehen wir uns an, wofür sie verwendet wird und wann eine Variable typisiert werden muss.

Standardisierung wird hauptsächlich verwendet, um die Werte von Verteilungen mit unterschiedlichen Mittelwerten und Varianzen zu vergleichen. In ähnlicher Weise wird die Standardisierung auch zur Berechnung einer Wahrscheinlichkeit verwendet.

Durch die Standardisierung zweier Werte von Verteilungen mit unterschiedlichen Eigenschaften können wir sehen, welcher Wert im Verhältnis zur gesamten Verteilung größer oder kleiner ist. Mit anderen Worten: Durch die Anwendung des Typisierungsprozesses können wir erkennen, welcher Wert dem Mittelwert seiner Verteilung am nächsten oder am weitesten davon entfernt ist.

Darüber hinaus ermöglicht die Typisierung, wie oben erläutert, auch die Berechnung von Wahrscheinlichkeiten, da Wahrscheinlichkeitstabellen im Allgemeinen auf einer typisierten Verteilung basieren.

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen