U-steuerkarte

Von Dr. Benjamin Anderson August 1, 2023 Qualitätsmanagement Keine Kommentare

In diesem Artikel erklären wir Ihnen, was eine U-Steuerkarte ist, welche Eigenschaften sie hat und wofür sie verwendet wird. Darüber hinaus können Sie sehen, wie eine U-Kontrollkarte erstellt und eine Übung Schritt für Schritt gelöst wird.

Was ist eine U-Kontrollkarte?

Eine U-Kontrollkarte , oder einfach U-Karte , ist eine Karte, die die Häufigkeit des Auftretens eines Phänomens pro Maßeinheit darstellt, wenn diese variabel ist.

Beispielsweise kann eine U-Kontrollkarte verwendet werden, um die Anzahl der Fehler pro Quadratmeter Stoff zu kontrollieren. Stoffproben können oft nicht mit der gleichen Oberfläche entnommen werden, sodass jede Probe anders ist. Somit ermöglicht uns das U-Diagramm die Untersuchung von Prozessen mit unterschiedlicher Stichprobengröße.

Es ist wichtig zu beachten, dass die U-Kontrollkarte nicht die Anzahl der fehlerhaften Einheiten darstellt, sondern wie in der C-Karte die Anzahl der Fehler, die jede Einheit aufweist. Im Gegensatz dazu kontrolliert eine P- oder NP-Regelkarte den Anteil und die Anzahl fehlerhafter Produkte. Im Folgenden betrachten wir die Unterschiede zwischen allen Arten von Kontrollkarten.

Bedenken Sie, dass das mathematische Referenzmodell der U-Kontrollkarte die Poisson-Verteilung ist, da wir die Anzahl des Auftretens eines Phänomens pro Maßeinheit untersuchen.

➤ Siehe: Fischverteilung

So erstellen Sie ein U-Kontrolldiagramm

Nachdem wir nun die Definition der U-Kontrollkarte kennen, sehen wir uns an, wie diese Art von Kontrollkarte erstellt wird:

Probenentnahme : Zunächst müssen verschiedene Proben entnommen werden, um die Entwicklung des zu messenden Phänomens zu verfolgen. Die Proben müssen gleich groß sein, außerdem empfiehlt sich die Entnahme von mindestens 20 Proben.
Bestimmen Sie, wie oft das Phänomen pro Maßeinheit auftritt : Für jede Probe wird angegeben, wie oft das zu untersuchende Phänomen wiederholt wird.
Berechnen Sie den Durchschnittswert des Auftretens : Aus den gesammelten Daten muss der Durchschnitt der Häufigkeit des Auftretens des Phänomens pro Maßeinheit berechnet werden.

$\overline{u}=\cfrac{\text{N\'umero de veces que ocurre el fen\'omeno}}{\text{N\'umero total de unidades de todas las muestras}}$

Berechnen Sie die U-Card-Kontrollgrenzen – Die U-Card-Kontrollgrenzen sollten dann anhand der unten angegebenen Formeln berechnet werden. Beachten Sie, dass der Wert der Kontrollgrenzen je nach Stichprobengröße variiert.

$\displaystyle LCS_i=\overline{u}+3\sqrt{\frac{\overline{u}}{n_i}$

$\displaystyle LCI_i=\overline{u}-3\sqrt{\frac{\overline{u}}{n_i}$

Gold

$LCS_i$

Und

$LCI_i$

sind jeweils die oberen und unteren Kontrollgrenzen der Probe i,

$\overline{u}$

ist der Durchschnittswert der Vorkommnisse und

$n_i$

ist die Stichprobengröße i.

Werte auf der Karte eintragen – Die gesammelten Werte zusammen mit den berechneten Kontrollgrenzen müssen nun auf einer Karte eingezeichnet werden, um die U-Kontrollkarte zu erstellen.
Analysieren Sie die U-Kontrollkarte : Letztlich muss nur noch überprüft werden, dass kein Wert auf der Karte die Kontrollgrenzen überschreitet und somit der Prozess unter Kontrolle ist. Andernfalls müssen Maßnahmen zur Korrektur des Prozesses ergriffen werden.

Beispiel einer U-Steuerkarte

Ein Industrieunternehmen möchte die Anzahl der Fehler pro ^m2 Stoff kontrollieren. Die folgende Tabelle zeigt die analysierten Proben und die Anzahl der festgestellten Mängel. Erstellen Sie eine U-Kontrollkarte, um die Anzahl der Fehler zu untersuchen.

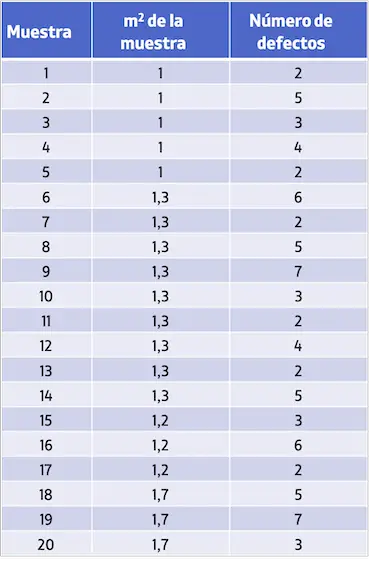
Um die U-Kontrollkarte zu erstellen, müssen Sie zunächst den Durchschnittswert der Anzahl der Fehler pro Probe berechnen:

$\overline{u}=\cfrac{\text{N\'umero de veces que ocurre el fen\'omeno}}{\text{N\'umero total de unidades}}=\cfrac{78}{25,4}=3,07$

Wir müssen nun die Kontrollgrenzen für jede Probe berechnen . Als Beispiel werden im Folgenden die Kontrollgrenzen für die erste Probe berechnet:

$\displaystyle LCS_1=\overline{u}+3\sqrt{\frac{\overline{u}}{n_1}}=3,07+3\sqrt{\frac{3,07}{1}}=8,33$

$\displaystyle LCI_1=\overline{u}-3\sqrt{\frac{\overline{u}}{n_1}}=3,07-3\sqrt{\frac{3,07}{1}}=-2,19$

Alle unteren Kontrollgrenzen führen zu einer negativen Zahl, was keinen Sinn ergibt. Daher werden wir die unteren Eingriffsgrenzen auf 0 setzen.

Somit sind die Werte der Kontrollgrenzen für jede Probe wie folgt:

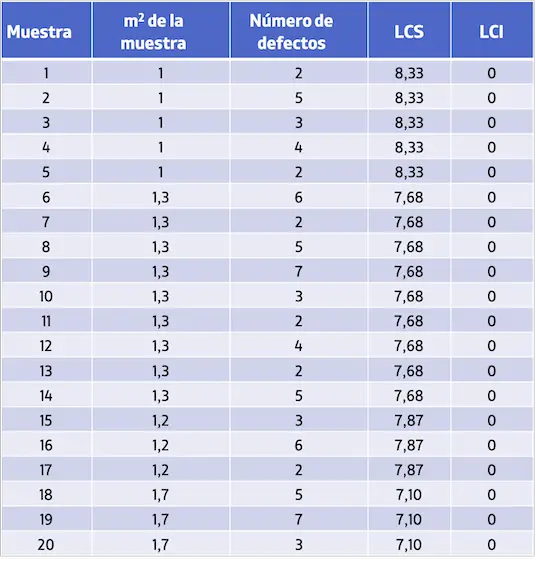
Schließlich reicht es aus, alle Werte in einem Diagramm darzustellen, um die Kontrollkarte U zu erhalten:

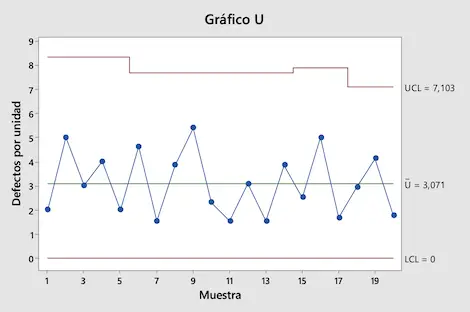
Wie Sie in der von uns erstellten U-Karte sehen können, liegen alle Werte innerhalb der Kontrollgrenzen. Daraus lässt sich schließen, dass der Produktionsprozess unter Kontrolle ist.

Andere Arten von Regelkarten

Neben der U-Karte gibt es noch andere Arten von Attributkontrollkarten:

P-Kontrollkarte : Der Anteil fehlerhafter Produkte wird kontrolliert.
NP-Kontrollkarte : Die Anzahl fehlerhafter Produkte wird kontrolliert.
Kontrolldiagramm C : Die Anzahl der Fehler wird wie in Diagramm U kontrolliert, die Stichprobengröße bleibt jedoch konstant.

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen