Unabhängige variable

In diesem Artikel wird erklärt, was unabhängige Variablen sind. So finden Sie die Bedeutung einer unabhängigen Variablen in Mathematik und Statistik und sehen auch einige Beispiele für diesen Variablentyp.

Was ist eine unabhängige Variable?

Eine unabhängige Variable ist eine Variable, deren Wert nicht vom Wert einer anderen Variablen abhängt. Im Gegenteil: Wenn eine unabhängige Variable ihren Wert ändert, ändert sie auch den Wert einer abhängigen Variablen.

Wenn Sie eine unabhängige Variable grafisch darstellen, wird sie normalerweise durch den Buchstaben x und auf der x-Achse (horizontale Achse) dargestellt.

Beispielsweise ist die Dauer der Miete einer Immobilie eine unabhängige Variable, die sich auf den von Ihnen gezahlten Preis auswirkt. Denn die Mietdauer ist bestimmbar und ihr Wert beeinflusst die preisabhängige Variable, denn je länger die Einrichtungen genutzt werden, desto mehr müssen sie zahlen.

Unabhängige Variablen können auch erklärende Variablen, Eingabevariablen oder manipulierte Variablen genannt werden.

Beispiele für unabhängige Variablen

Nachdem wir die Definition einer unabhängigen Variablen kennengelernt haben, schauen wir uns nun einige Beispiele dieser Art von Variablen an, um das Konzept besser zu verstehen.

• Die Lernzeit (unabhängige Variable) hat Einfluss auf die erzielten Noten (abhängige Variable).
• Der Preis eines Produkts (unabhängige Variable) verändert die Anzahl der Personen, die bereit sind, das Produkt zu kaufen (abhängige Variable).
• Die Umgebungstemperatur (unabhängige Variable) beeinflusst die Anzahl der Waldbrände (abhängige Variable).
• Werbung für ein Produkt (unabhängige Variable) hat Einfluss auf die Anzahl der Verkäufe dieses Produkts (abhängige Variable).
• Die Einwohnerzahl einer Stadt (unabhängige Variable) ist mit der Anzahl der Taxis in einer Stadt (abhängige Variable) verknüpft.

Unabhängige Variable in der Mathematik

In der Mathematik wird eine Ursache-Wirkungs-Beziehung üblicherweise mithilfe einer unabhängigen Variablen und einer abhängigen Variablen modelliert. Somit definiert eine Funktion die mathematische Beziehung, die zwischen der unabhängigen Variablen und der abhängigen Variablen besteht.

Unabhängige Variablen werden normalerweise durch den Buchstaben x dargestellt, während für abhängige Variablen der Buchstabe y verwendet wird.

Beispielsweise gibt die Funktion y=2x an, dass die abhängige Variable y doppelt so stark zunimmt, wenn die unabhängige Variable x um eine Einheit zunimmt.

Um mehr über mathematische Funktionen zu erfahren, empfehlen wir den Besuch unserer Partner-Website function.xyz .

Unabhängige Variablen in der Statistik

In der Realität ist es jedoch sehr schwierig, eine Beziehung zwischen zwei Variablen zu finden, die durch eine exakte mathematische Funktion definiert werden kann, da manchmal der gleiche Wert einer unabhängigen Variablen zu einem anderen Wert der abhängigen Variablen führt.

Wenn wir zum Beispiel mehr lernen, bekommen wir manchmal eine schlechtere Note, oder umgekehrt, wenn wir weniger lernen, bekommen wir eine bessere Note. Daher ist nicht nur die Anzahl der Stunden, die wir mit dem Lernen verbringen, ein Faktor, der die erzielte Note beeinflusst, sondern sie kann auch abhängig von der Schwierigkeit der Prüfung oder der Schwierigkeit des untersuchten Fachs variieren.

Daher werden in der Statistik üblicherweise viele Experimente durchgeführt, um festzustellen, ob eine Beziehung zwischen einer unabhängigen Variablen und einer abhängigen Variablen besteht. Die erhaltenen Ergebnisse können dann grafisch dargestellt werden, um zu überprüfen, ob die Variablen verknüpft sind, und wenn ja, welche Art von Beziehung sie haben (positiv, negativ, linear, exponentiell usw.).

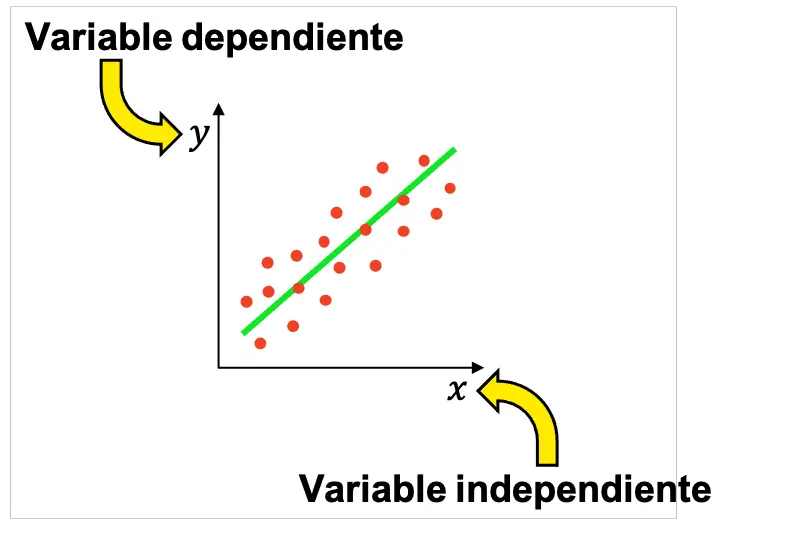
Bedenken Sie, dass es in einer Umfrage mehr als eine unabhängige Variable geben kann, obwohl die grundlegendsten statistischen Studien mit einer unabhängigen und einer abhängigen Variablen durchgeführt werden.

Sobald die statistische Untersuchung durchgeführt wurde, kann eine mathematische Funktion berechnet werden, die es ermöglicht, eine Näherung vorzunehmen und so den Zusammenhang zwischen den Variablen zu modellieren. Normalerweise erstellt man also zuerst ein statistisches Modell und dann ein mathematisches Modell.