Einfaktorielle oder zweifaktorielle anova: wann sollten sie verwendet werden?
Eine ANOVA , kurz für „Analysis of Variance“, wird verwendet, um zu bestimmen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr unabhängigen Gruppen besteht oder nicht.
Die beiden häufigsten ANOVA-Typen sind die einfaktorielle ANOVA und die zweifaktorielle ANOVA.
Einfaktorielle ANOVA: Wird verwendet, um zu bestimmen, wie sich ein Faktor auf eine Antwortvariable auswirkt.

Zweifaktorielle ANOVA: Wird verwendet, um zu bestimmen, wie sich zwei Faktoren auf eine Antwortvariable auswirken und um zu bestimmen, ob zwischen den beiden Faktoren eine Wechselwirkung auf die Antwortvariable besteht oder nicht.
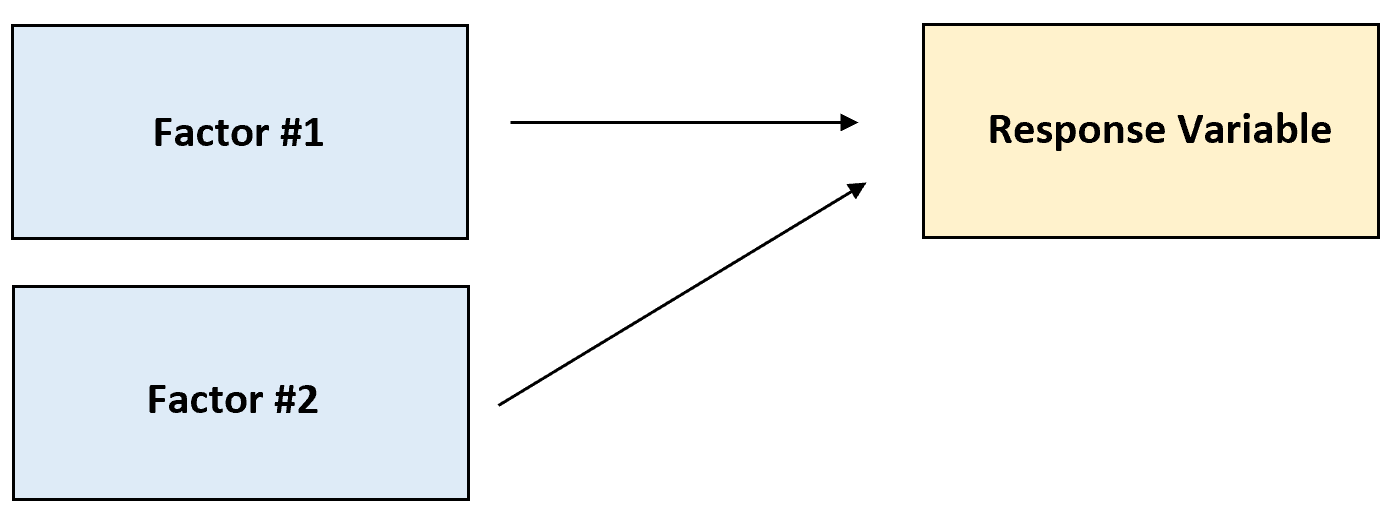
Die folgenden Beispiele zeigen, wie die einzelnen ANOVA-Typen durchgeführt werden.
Beispiel: Einfaktorielle ANOVA
Angenommen, ein Professor möchte wissen, ob drei verschiedene Lerntechniken zu unterschiedlichen Testergebnissen führen. Um dies zu testen, rekrutiert er 30 Studenten für die Teilnahme an einer Studie und bittet jeden nach dem Zufallsprinzip, eine von drei Techniken zur Vorbereitung auf eine Prüfung anzuwenden. Nach einem Monat absolvieren alle Schüler den gleichen Test.
Die Testergebnisse jedes Schülers sind unten aufgeführt:
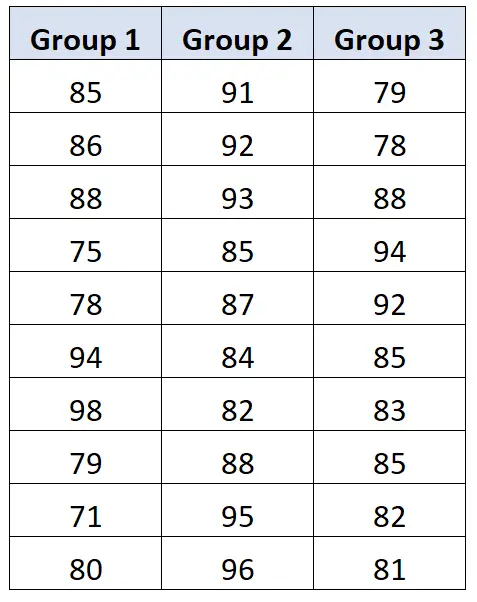
Der Professor führt eine einfaktorielle ANOVA durch und erhält folgende Ergebnisse:
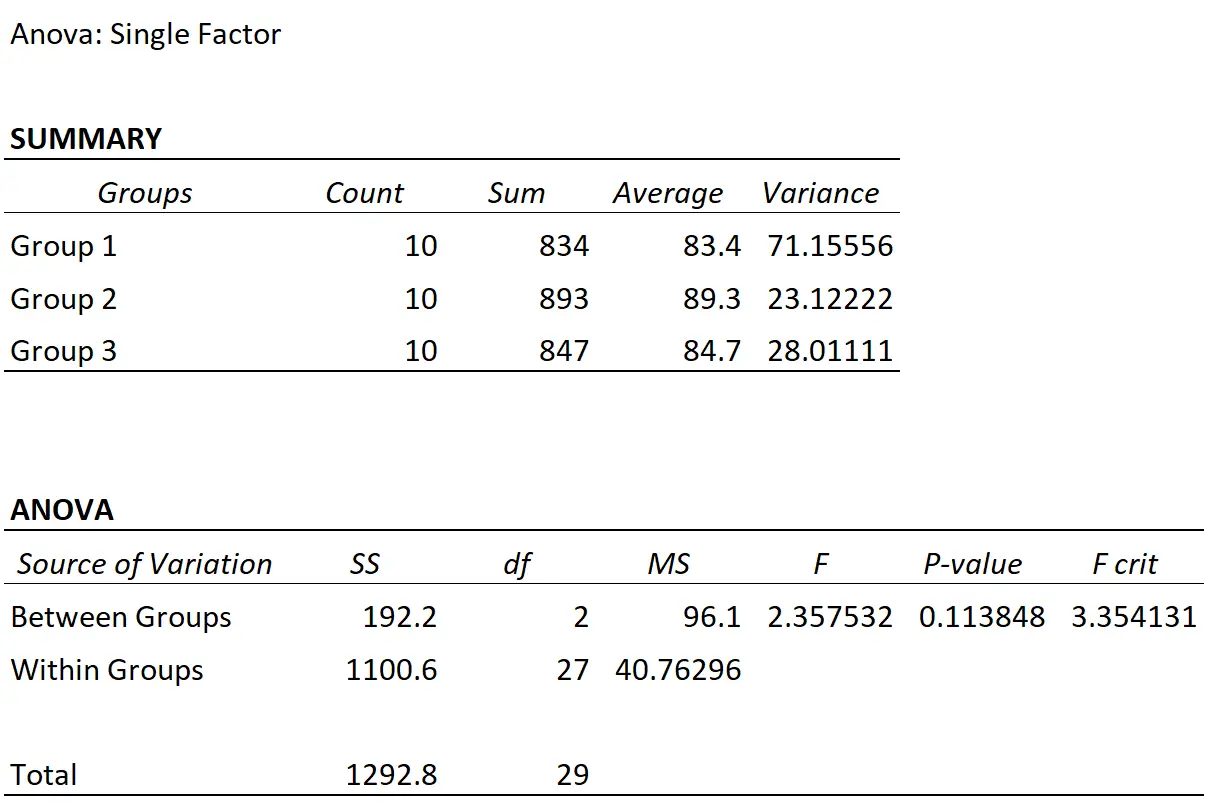
Die F-Test-Statistik beträgt 2,3575 und der entsprechende p-Wert beträgt 0,1138 . Da dieser p-Wert nicht weniger als 0,05 beträgt, haben wir keine ausreichenden Beweise dafür, dass die drei Lerntechniken zu unterschiedlichen durchschnittlichen Prüfungsergebnissen führen.
Beispiel: Zweifaktorielle ANOVA
Angenommen, ein Botaniker möchte wissen, ob das Pflanzenwachstum durch die Sonneneinstrahlung und die Häufigkeit des Gießens beeinflusst wird. Sie pflanzt 40 Samen und lässt sie zwei Monate lang unter unterschiedlichen Bedingungen der Sonneneinstrahlung und Bewässerungshäufigkeit wachsen. Nach zwei Monaten zeichnet sie die Höhe jeder Pflanze auf. Die Ergebnisse sind unten dargestellt:
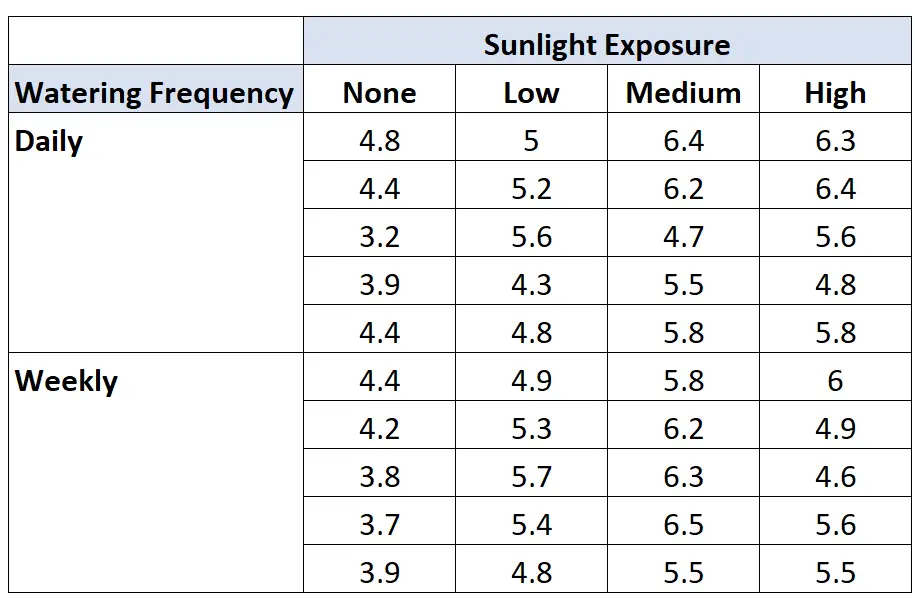
Der Professor führt eine zweifaktorielle ANOVA durch und erhält folgende Ergebnisse:
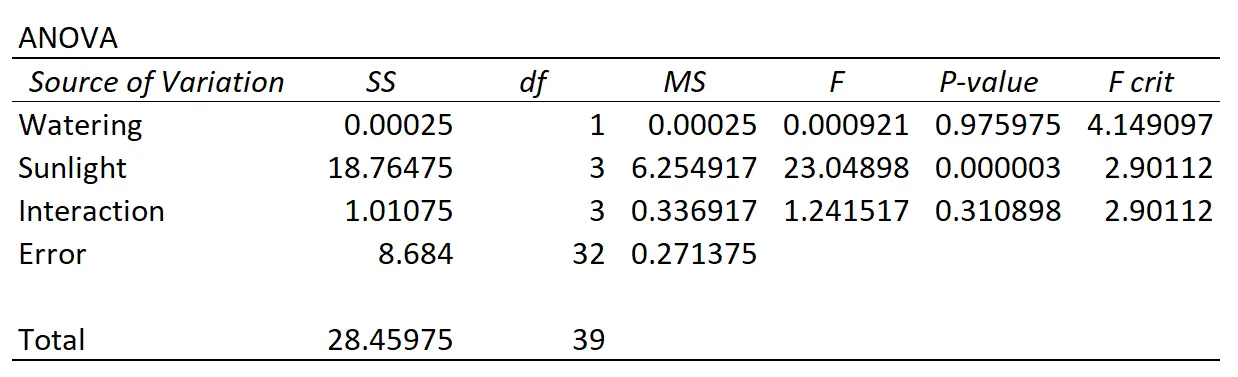
So interpretieren Sie die Ergebnisse:
- Der p-Wert für die Wechselwirkung zwischen Bewässerungshäufigkeit und Sonneneinstrahlung betrug 0,310898 . Dies ist auf dem Alpha-Niveau von 0,05 statistisch nicht signifikant.
- Der p-Wert für die Bewässerungshäufigkeit betrug 0,975975 . Dies ist auf dem Alpha-Niveau von 0,05 statistisch nicht signifikant.
- Der p-Wert für Sonnenexposition betrug 0,000003 . Dies ist statistisch signifikant bei einem Alpha-Wert von 0,05.
Diese Ergebnisse deuten darauf hin, dass die Sonneneinstrahlung der einzige Faktor ist, der einen statistisch signifikanten Einfluss auf die Pflanzenhöhe hat.
Und da es keinen Wechselwirkungseffekt gibt, ist der Effekt der Sonneneinstrahlung bei jeder Bewässerungshäufigkeit gleichbleibend. Einfach ausgedrückt: Ob eine Pflanze täglich oder wöchentlich gegossen wird, hat keinen Einfluss darauf, wie sich Sonneneinstrahlung auf eine Pflanze auswirkt.
Praktisch: Welche ANOVA sollten Sie verwenden?
Verwenden Sie die folgenden Übungsaufgaben, um besser zu verstehen, wann Sie eine einfaktorielle oder zweifaktorielle ANOVA verwenden sollten.
Problem Nr. 1: Landwirtschaft
Ein Landwirt möchte wissen, ob drei verschiedene Düngemittel zu unterschiedlichen Erträgen führen. Um dies zu testen, streut er jede Art von Dünger auf zehn verschiedenen Feldern aus und misst den Gesamtertrag am Ende der Vegetationsperiode.
Welche Art von ANOVA sollte er verwenden, um festzustellen, ob unterschiedliche Düngemittel zu unterschiedlichen Ernteerträgen führen?
Antwort: Er sollte eine einfaktorielle ANOVA verwenden, da er nur einen Faktor berücksichtigt: Dünger. Eine einfaktorielle ANOVA kann ihm sagen, ob es einen statistisch signifikanten Unterschied in den Ernteerträgen zwischen den drei verschiedenen Düngemitteltypen gibt oder nicht.
Problem Nr. 2: Biologie
Ein Biologe möchte wissen, wie sich unterschiedliche Bodenniveaus (niedrig, mittel, hoch) und Bewässerungshäufigkeiten (wöchentlich, monatlich) auf das Wachstum einer bestimmten Pflanze auswirken.
Welche Art von ANOVA sollte verwendet werden, um zu bestimmen, ob unterschiedliche Kombinationen von Sonneneinstrahlung und Bewässerungshäufigkeit zu unterschiedlichem Pflanzenwachstum führen?
Antwort: Sie sollte eine Zwei-Wege-ANOVA verwenden, da sie zwei Faktoren berücksichtigt: Sonneneinstrahlung und Bewässerungshäufigkeit. Eine zweifaktorielle ANOVA kann Aufschluss darüber geben, ob unterschiedliche Werte jedes Faktors das Pflanzenwachstum unterschiedlich beeinflussen und ob es einen Wechselwirkungseffekt zwischen Sonnenlicht und Bewässerungshäufigkeit auf das Pflanzenwachstum gibt oder nicht.
Problem Nr. 3: Medikamente
Ein medizinischer Forscher möchte wissen, ob vier verschiedene Medikamente bei Patienten unterschiedliche durchschnittliche Blutdrucksenkungen bewirken. Dabei werden 20 Patienten nach dem Zufallsprinzip ausgewählt, um jedes Medikament einen Monat lang einzunehmen, und dann wird die Blutdrucksenkung bei jedem Patienten gemessen.
Welche Art von ANOVA sollte verwendet werden, um festzustellen, ob die vier verschiedenen Medikamente unterschiedliche Auswirkungen auf die Senkung des Blutdrucks haben?
Antwort: Er sollte eine einfaktorielle ANOVA verwenden, da er nur einen Faktor berücksichtigt: die Art der Medikation. Eine einfaktorielle ANOVA kann ihm sagen, ob es einen statistisch signifikanten Unterschied in der durchschnittlichen Blutdrucksenkung zwischen den vier Arten von Medikamenten gibt oder nicht.
Zusätzliche Ressourcen
Verwenden Sie die folgenden Tutorials, um die einfaktorielle ANOVA besser zu verstehen:
- Eine Einführung in die einfaktorielle ANOVA
- So führen Sie eine einfaktorielle ANOVA in Excel durch
- So führen Sie eine einfaktorielle ANOVA in R durch
Und nutzen Sie diese Tutorials, um die zweifaktorielle ANOVA besser zu verstehen: