Validierungssatz und testsatz: was ist der unterschied?

Wenn wir einen Algorithmus für maschinelles Lernen an einen Datensatz anpassen, unterteilen wir den Datensatz normalerweise in drei Teile:

1. Trainingssatz : Wird zum Trainieren des Modells verwendet.

2. Validierungssatz : Wird zur Optimierung der Modellparameter verwendet.

3. Testsatz : Wird verwendet, um eine unvoreingenommene Schätzung der endgültigen Modellleistung zu erhalten.

Das folgende Diagramm bietet eine visuelle Erklärung dieser drei verschiedenen Arten von Datensätzen:

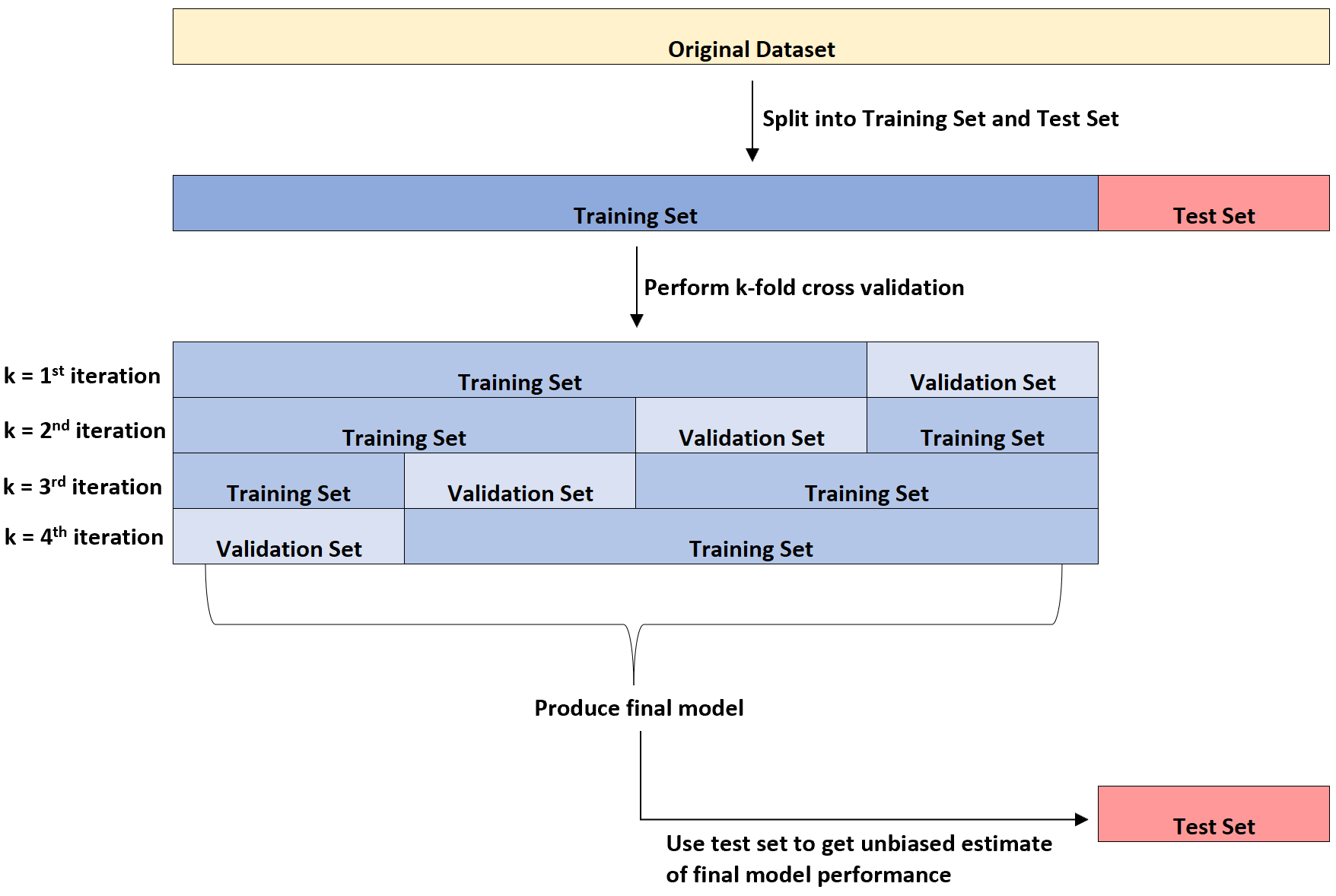
Ein Punkt, der für Studierende Verwirrung stiftet, ist der Unterschied zwischen dem Validierungssatz und dem Testsatz.

Einfach ausgedrückt wird der Validierungssatz zur Optimierung der Modellparameter verwendet, während der Testsatz dazu dient, eine unvoreingenommene Schätzung des endgültigen Modells bereitzustellen.

Es kann gezeigt werden, dass die durch k-fache Kreuzvalidierung gemessene Fehlerrate dazu neigt, die tatsächliche Fehlerrate zu unterschätzen, sobald das Modell auf einen unsichtbaren Datensatz angewendet wird.

Daher passen wir das endgültige Modell an den Testsatz an , um eine unvoreingenommene Schätzung der tatsächlichen Fehlerrate in der realen Welt zu erhalten.

Das folgende Beispiel veranschaulicht den Unterschied zwischen einem Validierungssatz und einem Testsatz in der Praxis.

Beispiel: Den Unterschied zwischen Validierungssatz und Testsatz verstehen

Nehmen wir an, ein Immobilieninvestor möchte (1) die Anzahl der Schlafzimmer, (2) die Gesamtquadratfußzahl und (3) die Anzahl der Badezimmer verwenden, um den Verkaufspreis eines bestimmten Hauses vorherzusagen.

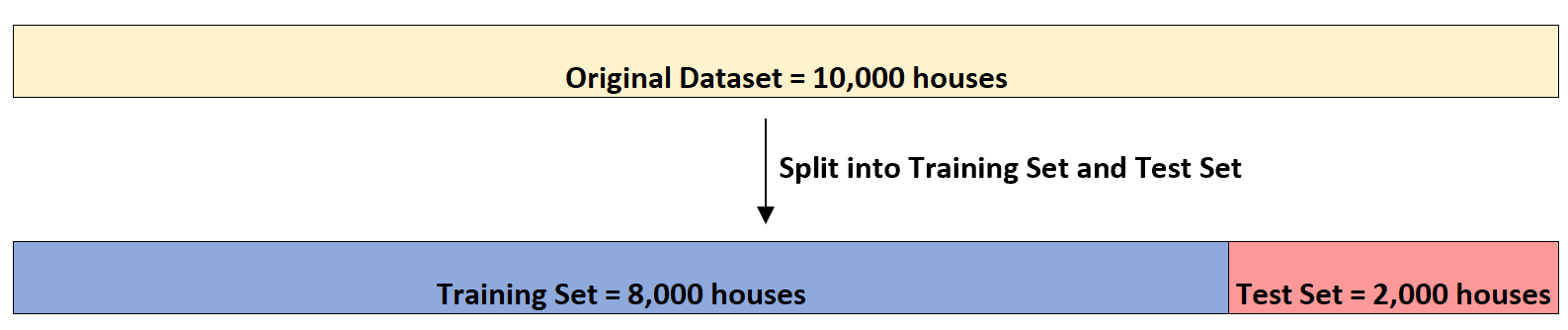
Nehmen wir an, er verfügt über einen Datensatz mit diesen Informationen zu 10.000 Häusern. Zunächst wird der Datensatz in einen Trainingssatz mit 8.000 Häusern und einen Testsatz mit 2.000 Häusern aufgeteilt:

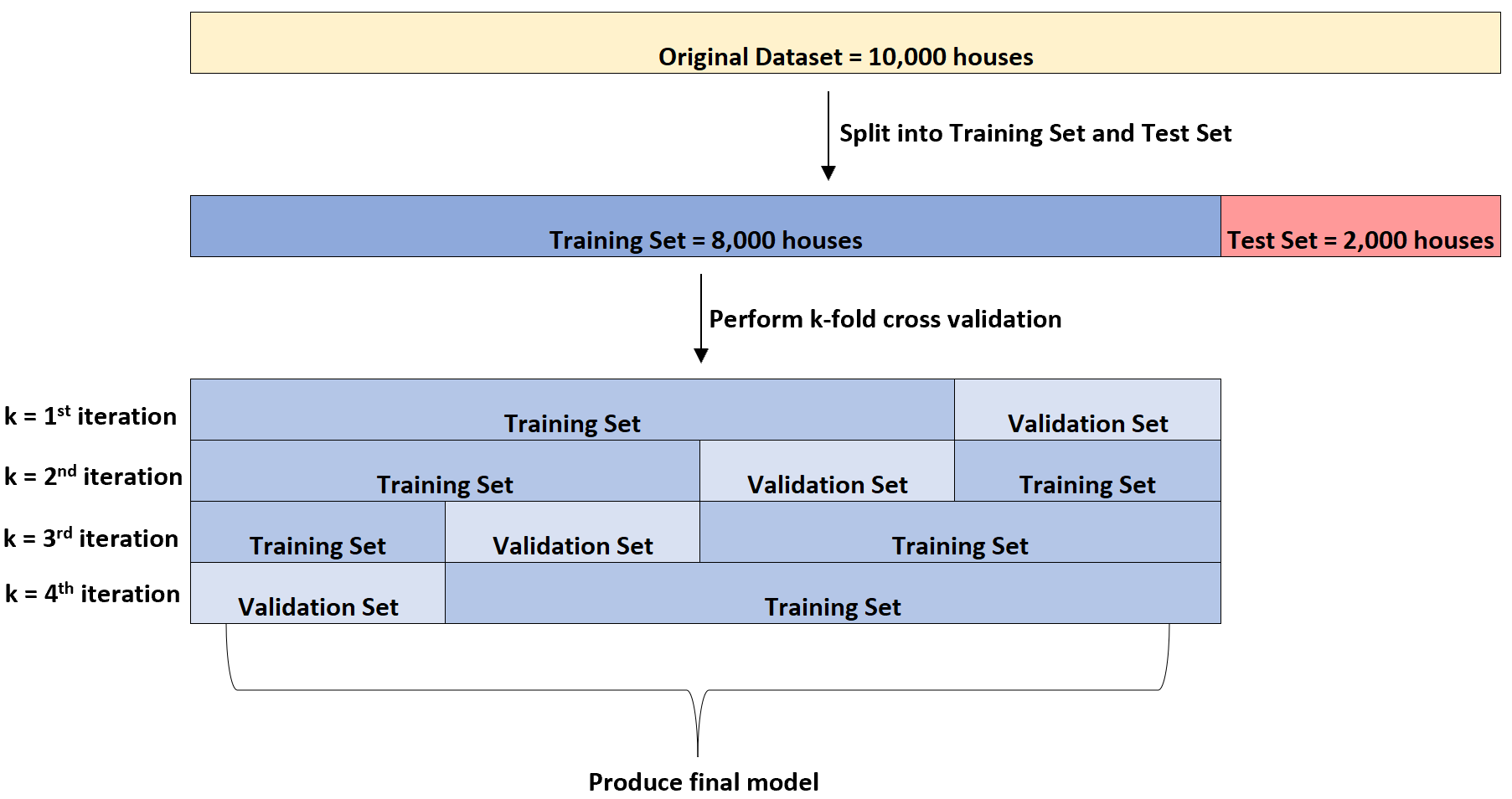
Anschließend wird viermal ein multiples lineares Regressionsmodell an den Datensatz angepasst. Es werden jedes Mal 6.000 Häuser für den Trainingssatz und 2.000 Häuser für den Validierungssatz verwendet.

Dies wird als k-fache Kreuzvalidierung bezeichnet.

Der Trainingssatz wird zum Trainieren des Modells und der Validierungssatz zur Bewertung der Leistung des Modells verwendet. Für den Validierungssatz wird jedes Mal eine andere Gruppe von 2.000 Häusern verwendet.

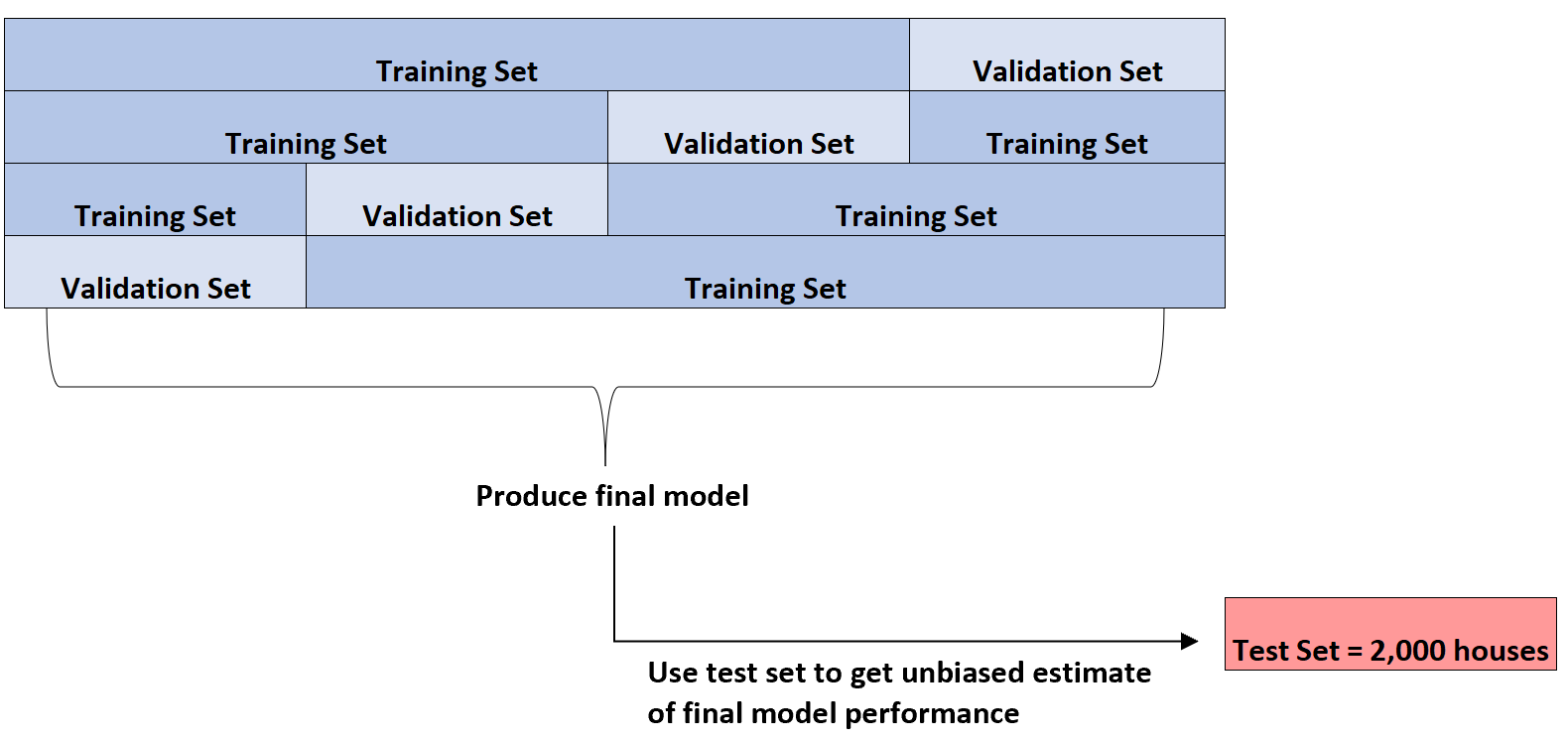
Es kann diese k-fache Kreuzvalidierung für mehrere verschiedene Arten von Regressionsmodellen durchführen, um das Modell zu identifizieren, das den geringsten Fehler aufweist (d. h. das Modell zu identifizieren, das am besten zum Datensatz passt).

Erst wenn das beste Modell ermittelt wurde, wird das zu Beginn vorgestellte 2.000-Haus-Testset verwendet, um eine unvoreingenommene Schätzung der endgültigen Leistung des Modells zu erhalten.

Es könnte beispielsweise einen bestimmten Typ eines Regressionsmodells identifizieren, dessen mittlerer absoluter Fehler 8,345 beträgt. Das heißt, die durchschnittliche absolute Differenz zwischen dem prognostizierten Immobilienpreis und dem tatsächlichen Immobilienpreis beträgt 8.345 $.

Anschließend kann er dieses exakte Regressionsmodell an die noch nicht verwendete Testmenge von 2.000 Häusern anpassen und feststellen, dass der durchschnittliche absolute Fehler des Modells 8,847 beträgt.

Somit beträgt die unvoreingenommene Schätzung des wahren mittleren absoluten Fehlers des Modells 8.847 $.

Zusätzliche Ressourcen

Eine einfache Anleitung zur K-Fold-Kreuzvalidierung
So führen Sie eine K-Fold-Kreuzvalidierung in Python durch
So führen Sie eine K-Fold-Kreuzvalidierung in R durch