So berechnen sie die varianz einer wahrscheinlichkeitsverteilung

Eine Wahrscheinlichkeitsverteilung gibt uns die Wahrscheinlichkeit an, mit der eine Zufallsvariable bestimmte Werte annimmt.

Die folgende Wahrscheinlichkeitsverteilung sagt uns beispielsweise die Wahrscheinlichkeit, dass eine bestimmte Fußballmannschaft in einem bestimmten Spiel eine bestimmte Anzahl Tore schießt:

Um die Varianz einer Wahrscheinlichkeitsverteilung zu ermitteln, können wir die folgende Formel verwenden:

σ ² = Σ(x _i -μ) ² * P(x _i )

Gold:

• x _i : Der ^i-te Wert
• μ: Der Mittelwert der Verteilung
• P(x _i ): Die Wahrscheinlichkeit des ^i-ten Werts

Betrachten Sie zum Beispiel unsere Wahrscheinlichkeitsverteilung für die Fußballmannschaft:

Die durchschnittliche Anzahl der Tore der Fußballmannschaft würde wie folgt berechnet:

μ = 0*0,18 + 1*0,34 + 2*0,35 + 3*0,11 + 4*0,02 = 1,45 Tore.

Wir könnten die Varianz dann wie folgt berechnen:

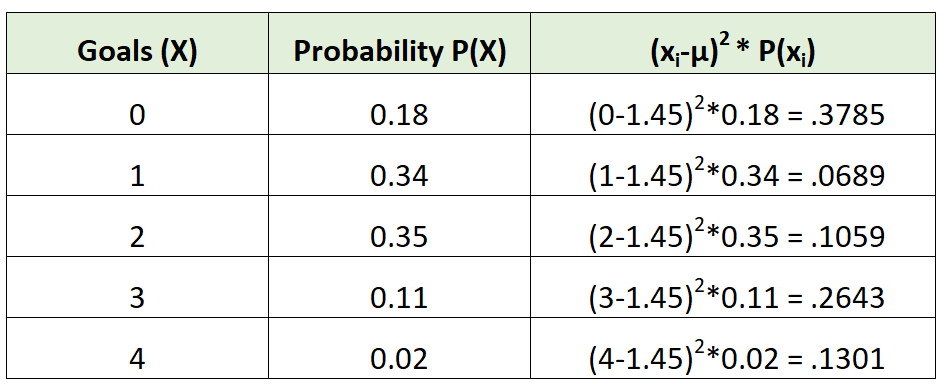
Die Varianz ist einfach die Summe der Werte in der dritten Spalte. Wir würden es also wie folgt berechnen:

^σ2 = 0,3785 + 0,0689 + 0,1059 + 0,2643 + 0,1301 = 0,9475

Die folgenden Beispiele zeigen, wie die Varianz einer Wahrscheinlichkeitsverteilung in einigen anderen Szenarien berechnet wird.

Beispiel 1: Unterschiedliche Fahrzeugpannen

Die folgende Wahrscheinlichkeitsverteilung gibt Auskunft über die Wahrscheinlichkeit, dass bei einem bestimmten Fahrzeug über einen Zeitraum von 10 Jahren eine bestimmte Anzahl von Batterieausfällen auftritt:

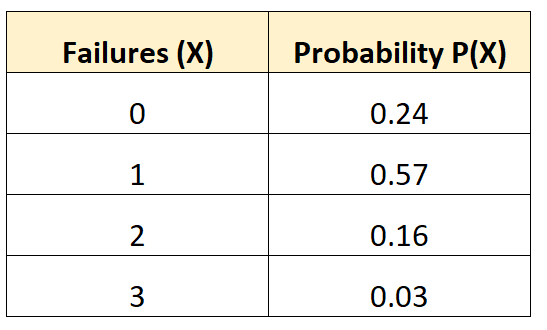
Um die Varianz dieser Wahrscheinlichkeitsverteilung zu ermitteln, müssen wir zunächst die durchschnittliche Anzahl erwarteter Ausfälle berechnen:

μ = 0*0,24 + 1*0,57 + 2*0,16 + 3*0,03 = 0,98 Ausfälle.

Wir könnten die Varianz dann wie folgt berechnen:

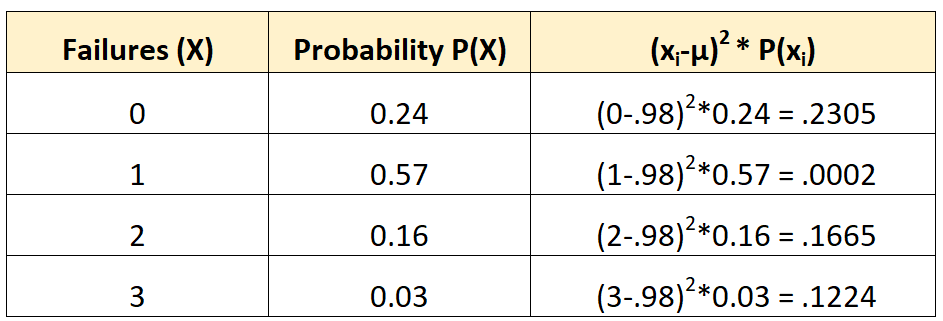
Die Varianz ist die Summe der Werte in der dritten Spalte. Wir würden es also wie folgt berechnen:

^σ2 = 0,2305 + 0,0002 + 0,1665 + 0,1224 = 0,5196

Beispiel 2: Verkaufsvariation

Die folgende Wahrscheinlichkeitsverteilung sagt uns die Wahrscheinlichkeit, dass ein bestimmter Verkäufer im kommenden Monat eine bestimmte Anzahl von Verkäufen tätigen wird:

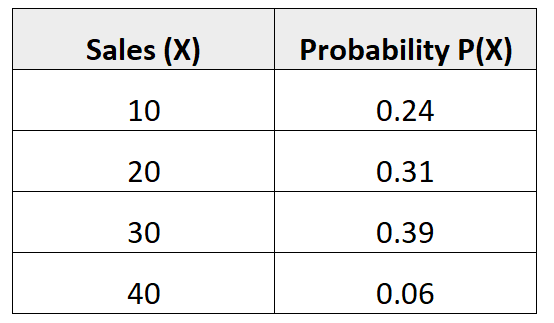
Um die Varianz dieser Wahrscheinlichkeitsverteilung zu ermitteln, müssen wir zunächst die durchschnittliche Anzahl der erwarteten Verkäufe berechnen:

μ = 10*0,24 + 20*0,31 + 30*0,39 + 40*0,06 = 22,7 verschmutzt.

Wir könnten die Varianz dann wie folgt berechnen:

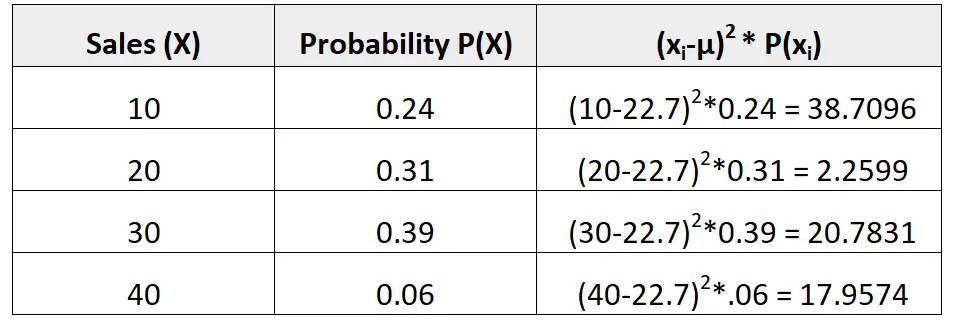
Die Varianz ist die Summe der Werte in der dritten Spalte. Wir würden es also wie folgt berechnen:

^σ2 = 38,7096 + 2,2599 + 20,7831 + 17,9574 = 79,71

Beachten Sie, dass wir auch den Wahrscheinlichkeitsverteilungsrechner verwenden könnten, um die Varianz dieser Verteilung automatisch zu berechnen:

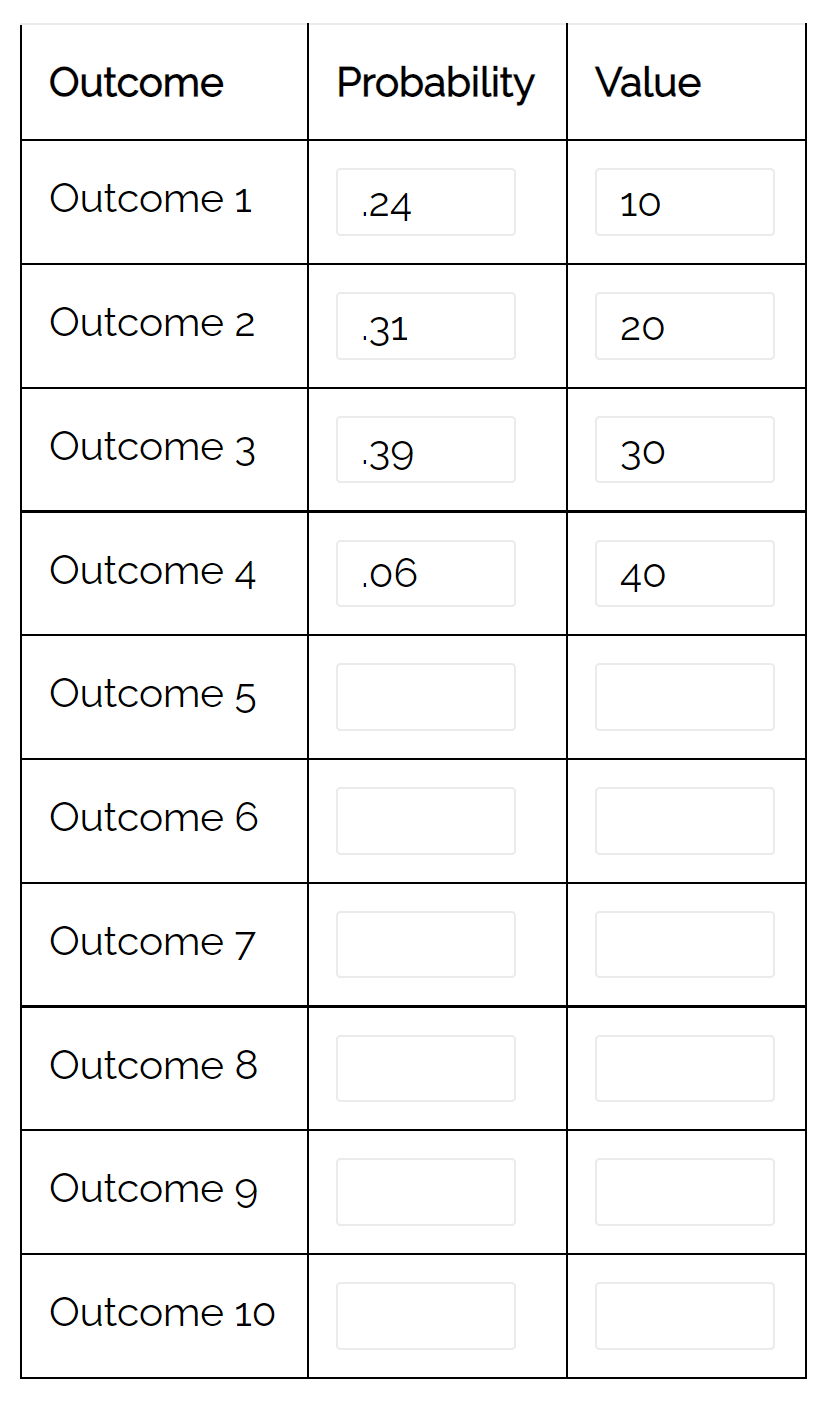
Der Unterschied beträgt 79,71 . Dies entspricht dem von uns manuell berechneten Wert.