So ermitteln sie die varianz gruppierter daten (mit beispiel)

Wir möchten oft die Varianz einer gruppierten Häufigkeitsverteilung berechnen.

Angenommen, wir haben die folgende gruppierte Häufigkeitsverteilung:

Obwohl es nicht möglich ist, die genaue Varianz zu berechnen, da wir die Rohdatenwerte nicht kennen, ist es möglich, die Varianz mithilfe der folgenden Formel zu schätzen:

Varianz: Σn _i (m _i -μ) ² / (N-1)

Gold:

• n _i : Die Häufigkeit der i- ^ten Gruppe
• _mi : Die Mitte der i- ^ten Gruppe
• μ : Der Durchschnitt
• N: Die Gesamtstichprobengröße

Hinweis: Der Mittelpunkt jeder Gruppe kann durch Bildung des Durchschnitts der unteren und oberen Werte des Bereichs ermittelt werden. Der Mittelpunkt der ersten Gruppe wird beispielsweise wie folgt berechnet: (1+10) / 2 = 5,5.

Das folgende Beispiel zeigt, wie diese Formel in der Praxis angewendet wird.

Beispiel: Berechnen Sie die Varianz gruppierter Daten

Angenommen, wir haben die folgenden gruppierten Daten:

So würden wir die zuvor erwähnte Formel verwenden, um die Varianz dieser gruppierten Daten zu berechnen:

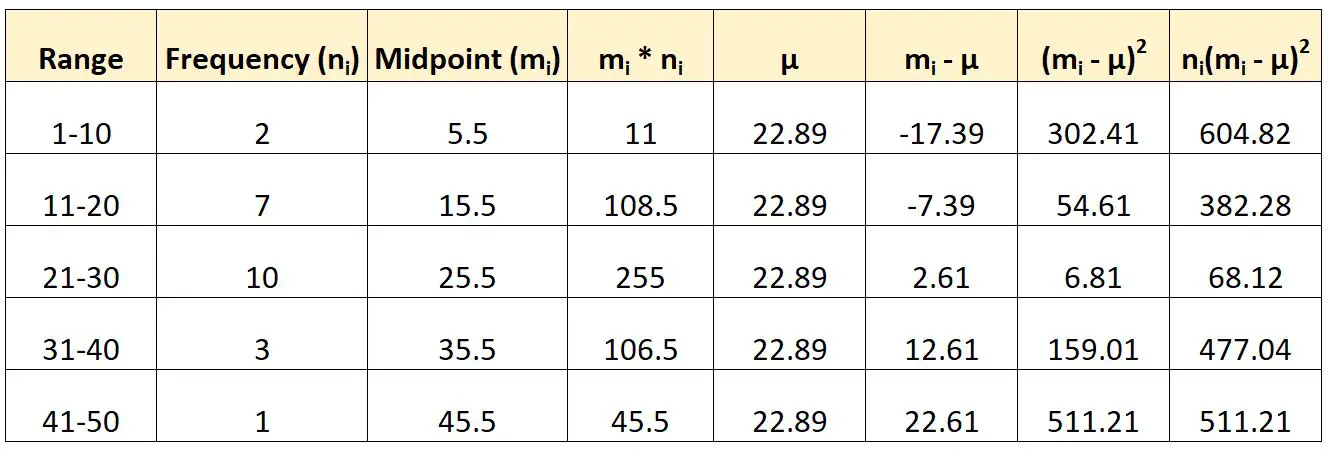
Wir würden dann die Varianz wie folgt berechnen:

• Varianz: Σn _i (m _i -μ) ² / (N-1)
• Differenz : (604,82 + 382,28 + 68,12 + 477,04 + 511,21) / (23-1)
• Differenz : 92,885

Die Varianz des Datensatzes beträgt 92,885 .

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere Metriken für gruppierte Daten berechnen:

So ermitteln Sie den Mittelwert und die Standardabweichung gruppierter Daten
So berechnen Sie die Perzentilrangfolge für gruppierte Daten
So ermitteln Sie den Median gruppierter Daten
So finden Sie den gruppierten Datenmodus