So ermitteln sie den variationskoeffizienten auf einem ti-84-rechner

Ein Variationskoeffizient , oft mit CV abgekürzt, ist eine Möglichkeit, die Streuung von Werten in einem Datensatz relativ zum Mittelwert zu messen. Es wird wie folgt berechnet:

CV = σ / μ

Gold:

• σ: die Standardabweichung des Datensatzes
• μ: der Durchschnitt des Datensatzes

Vereinfacht ausgedrückt ist der Variationskoeffizient das Verhältnis der Standardabweichung zum Mittelwert.

Es wird häufig verwendet, um die Variation zwischen zwei verschiedenen Datensätzen zu vergleichen. Im Finanzwesen wird es beispielsweise verwendet, um die durchschnittliche erwartete Rendite einer Investition mit der erwarteten Standardabweichung der Investition zu vergleichen.

Angenommen, ein Anleger erwägt eine Investition in die folgenden zwei Investmentfonds:

Investmentfonds A: Mittelwert = 9 %, Standardabweichung = 12,4 %

OGAW B: Durchschnitt = 5 %, Standardabweichung = 8,2 %

Der Anleger kann den Variationskoeffizienten für jeden Fonds berechnen:

• CV für Investmentfonds A = 12,4 % / 9 % = 1,38
• CV für Investmentfonds B = 8,2 % / 5 % = 1,64

Da Investmentfonds A einen niedrigeren Variationskoeffizienten aufweist, bietet er im Vergleich zur Standardabweichung eine bessere Durchschnittsrendite.

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie der Variationskoeffizient für den folgenden Datensatz auf einem TI-84-Rechner berechnet wird:

Datensatz: 3, 8, 8, 13, 16, 11

Schritt 1: Geben Sie die Daten ein

Zuerst geben wir die Datenwerte ein.

Drücken Sie Stat und dann EDIT . Geben Sie dann die Datensatzwerte in Spalte L1 ein:

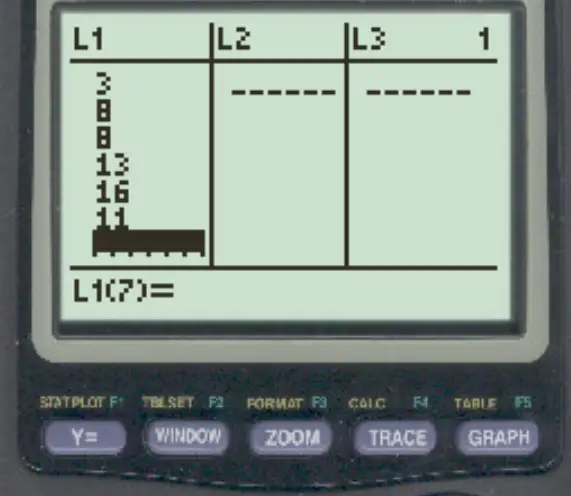
Schritt 2: Ermitteln Sie den Variationskoeffizienten

Tippen Sie anschließend auf Statistik , scrollen Sie dann nach rechts und tippen Sie auf CALC .

Tippen Sie dann auf 1-Var-Statistiken .

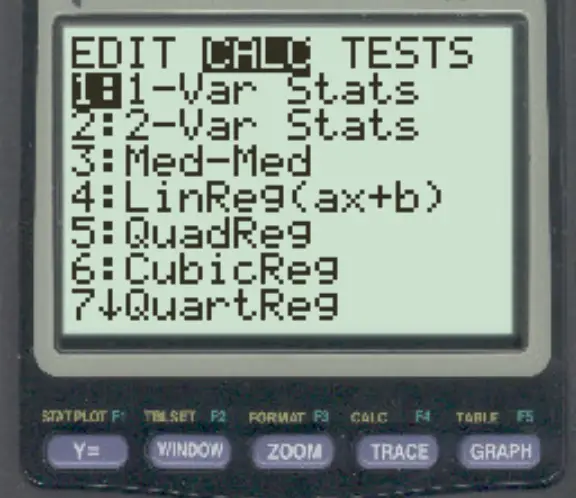
Drücken Sie im neuen Bildschirm, der angezeigt wird, die Eingabetaste .

Sobald Sie die Eingabetaste drücken, wird eine Liste mit zusammenfassenden Statistiken angezeigt:

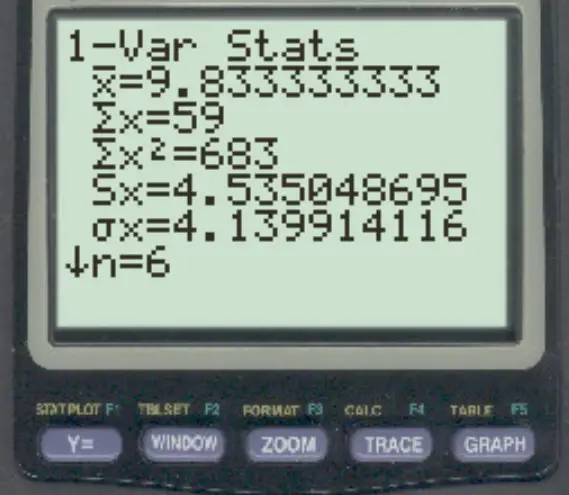
Auf diesem Bildschirm können wir den Stichprobenmittelwert und die Standardabweichungswerte beobachten:

• Durchschnitt ( x ): 9,8333
• Probenstandardabweichung (Sx): 4,535

Den Variationskoeffizienten können wir dann wie folgt berechnen:

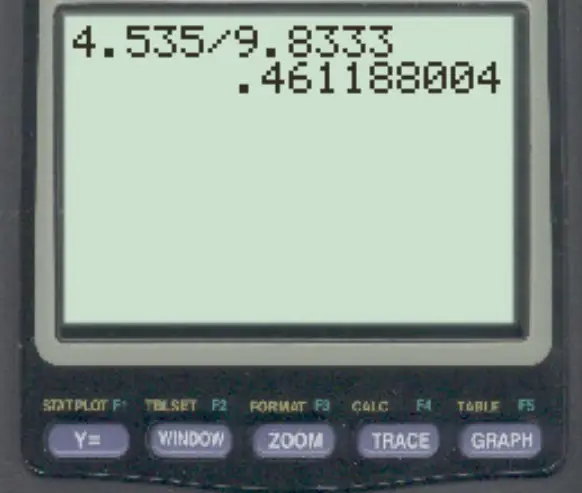
Der Variationskoeffizient für diesen Datensatz beträgt 0,4611 . In Prozent ausgedrückt entspricht dies 46,11 % .

Zusätzliche Ressourcen

So finden Sie eine fünfstellige Zusammenfassung auf einem TI-84-Rechner
So finden Sie den Interquartilbereich auf einem TI-84-Rechner