So vergleichen sie boxplots: mit beispielen

Ein Boxplot ist eine Art Diagramm, das die fünfstellige Zusammenfassung eines Datensatzes anzeigt, der Folgendes umfasst:

• Der Mindestwert
• Das erste Quartil (das 25. Perzentil)
• Der Medianwert
• Das dritte Quartil (das 75. Perzentil)
• Der Maximalwert

Um ein Boxplot zu erstellen, zeichnen wir eine Box vom ersten bis zum dritten Quartil. Als nächstes zeichnen wir eine vertikale Linie am Mittelwert. Abschließend zeichnen wir „Whisker“ der Quartile bis zum Minimal- und Maximalwert.

Boxplots sind nützlich, weil sie es uns ermöglichen, die Verteilung von Werten in einem Datensatz schnell zu verstehen. Sie eignen sich auch zum Vergleich zweier unterschiedlicher Datensätze.

Wenn wir zwei oder mehr Boxplots vergleichen, können wir vier verschiedene Fragen beantworten:

1. Wie vergleichen sich die Medianwerte? Wir können die vertikale Linie in jedem Feld vergleichen, um zu bestimmen, welcher Datensatz einen höheren Medianwert hat.

2. Wie ist die Streuung im Vergleich? Wir können die Länge jedes Kästchens vergleichen (die den Abstand zwischen Q1 und Q3 darstellt – den Interquartilbereich), um zu bestimmen, welcher Datensatz größer ist.

3. Wie lässt sich Asymmetrie vergleichen? Je näher die vertikale Linie am ersten Quartal liegt, desto positiver ist der Datensatz. Je näher die vertikale Linie am dritten Viertel liegt, desto verzerrter ist der Datensatz.

4. Sind Ausreißer vorhanden? In Boxplots werden Ausreißer normalerweise durch kleine Kreise dargestellt, die über jeden Whisker hinausragen. Eine Beobachtung wird als Ausreißer definiert, wenn sie eines der folgenden Kriterien erfüllt:

• Eine Beobachtung ist kleiner als Q1 – 1,5*IQR
• Eine Beobachtung ist größer als Q3 + 1,5*IQR

Das folgende Beispiel zeigt, wie man zwei verschiedene Boxplots vergleicht und diese vier Fragen beantwortet.

Beispiel: Vergleich von Boxplots

Die folgenden Datensätze zeigen die Ergebnisse von Studierenden, die eine von zwei Lerntechniken zur Prüfungsvorbereitung genutzt haben:

Methode 1: 78, 78, 79, 80, 80, 82, 82, 83, 83, 86, 86, 86, 86, 87, 87, 87, 88, 88, 88, 91

Methode 2: 66, 66, 66, 67, 68, 70, 72, 75, 75, 78, 82, 83, 86, 88, 89, 90, 93, 94, 95, 98

Wenn wir für jeden Datensatz Boxplots erstellen, würden diese wie folgt aussehen:

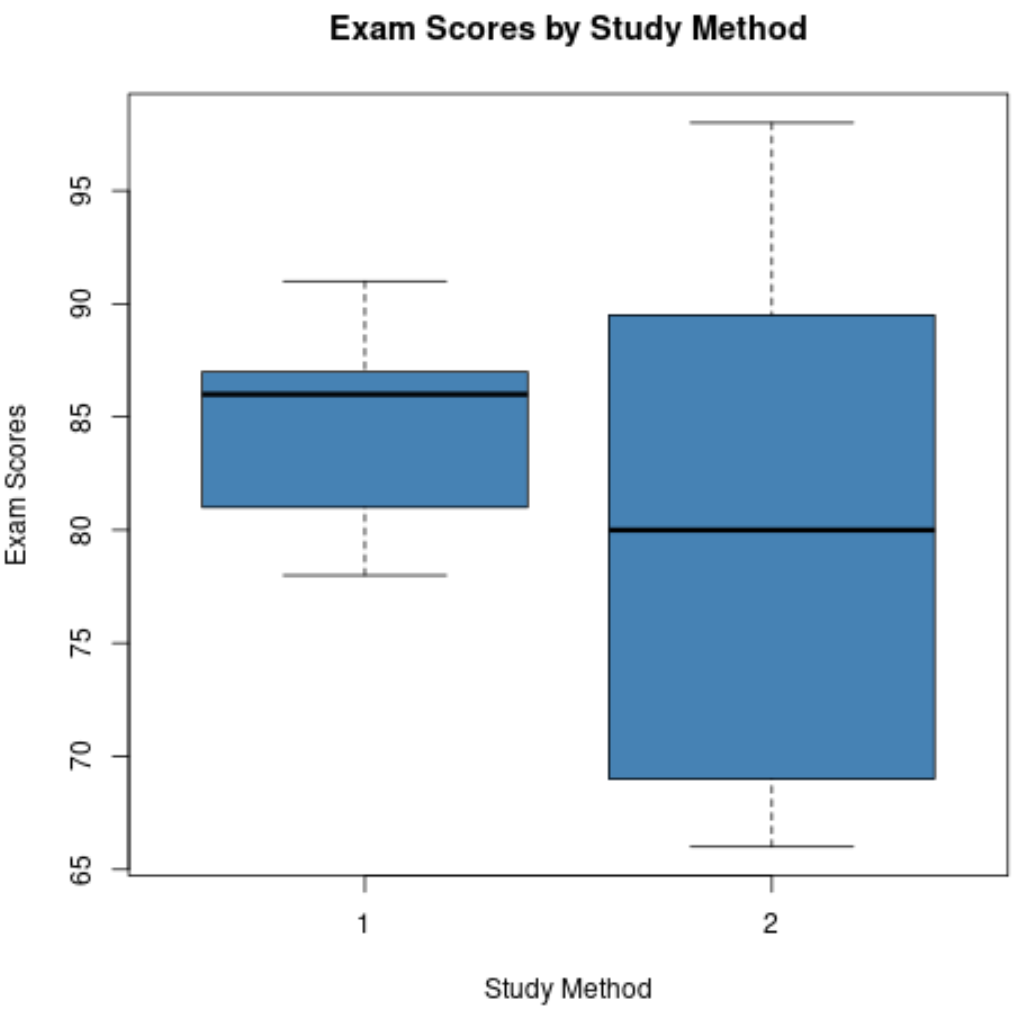
Wir können diese beiden Boxplots vergleichen und die folgenden vier Fragen beantworten:

1. Wie vergleichen sich die Medianwerte? Die Linie in der Mitte des Boxplots für Lernmethode 1 ist höher als die Linie für Lernmethode 2, was darauf hinweist, dass Studierende, die Lernmethode 1 verwendeten, bei einer höheren Prüfung eine Durchschnittsnote erzielten.

2. Wie ist die Streuung im Vergleich? Das Boxdiagramm für Lernmethode 2 ist viel länger als das für Lernmethode 1, was darauf hindeutet, dass die Prüfungsergebnisse unter den Studierenden, die Lernmethode 2 verwendet haben, viel stärker verteilt sind.

3. Wie lässt sich Asymmetrie vergleichen? Die Linie in der Mitte des Boxplots für Lernmethode 1 liegt nahe bei Q3, was darauf hinweist, dass die Verteilung der Prüfungsergebnisse für Studierende, die Lernmethode 1 verwendet haben, negativ verzerrt ist. Umgekehrt liegt die Linie in der Mitte des Boxplots für Studienmethode 2 nahe an der Mitte der Box, was bedeutet, dass die Verteilung der Ergebnisse nur minimal schief ist.

4. Sind Ausreißer vorhanden? Keiner der Boxplots weist winzige Kreise auf, die über die oberen oder unteren Whisker hinausragen, was bedeutet, dass keiner der Datensätze eindeutige Ausreißer aufweist.

Zusätzliche Ressourcen

So erstellen und interpretieren Sie Boxplots in Excel
So erstellen und interpretieren Sie Boxplots in SPSS
So erstellen Sie mehrere Boxplots in R
So erstellen und interpretieren Sie Boxplots in Stata