Vergleich der z-scores verschiedener verteilungen

Ein Z-Score gibt an, um wie viele Standardabweichungen ein einzelner Datenwert vom Mittelwert abweicht. Es wird wie folgt berechnet:

Z-Score = (x – μ) / σ

Gold:

• x: individueller Datenwert
• μ: Bevölkerungsdurchschnitt
• σ: Populationsstandardabweichung

Ein Z-Score für einen einzelnen Wert kann wie folgt interpretiert werden:

• Positiver Z-Score: Der Einzelwert liegt über dem Durchschnitt.
• Negativer Z-Score: Der Einzelwert ist niedriger als der Durchschnitt.
• Ein Z-Score von 0: Der Einzelwert entspricht dem Durchschnitt.

Z-Scores sind besonders nützlich, wenn wir die relative Position zweier Datenpunkte aus zwei verschiedenen Verteilungen vergleichen möchten. Um dies zu veranschaulichen, betrachten Sie das folgende Beispiel.

Beispiel: Vergleich von Z-Scores

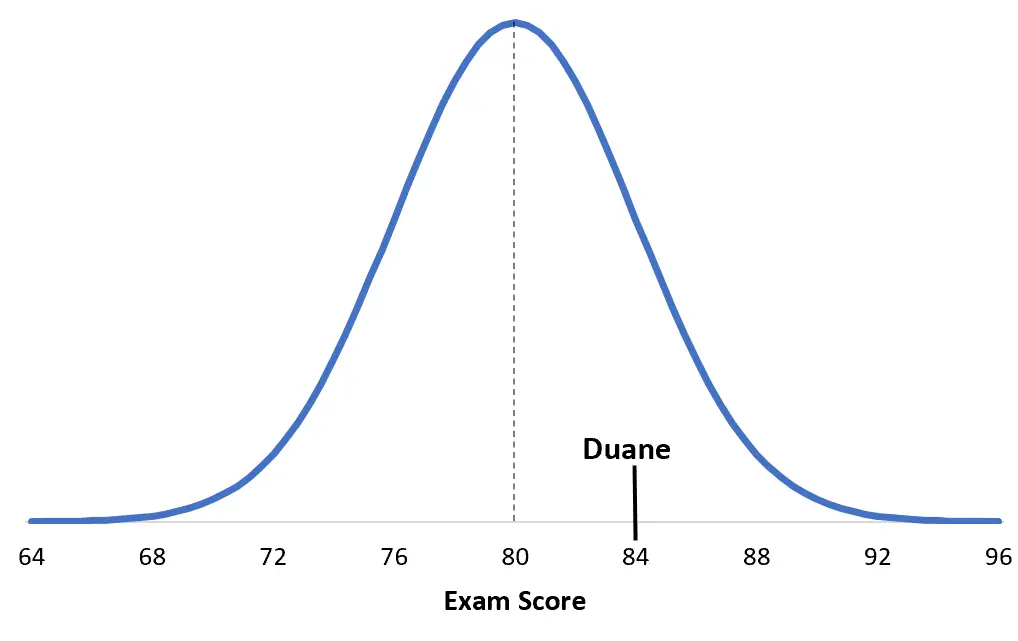
Die Ergebnisse einer bestimmten College-Prüfung sind normalverteilt mit dem Mittelwert μ = 80 und der Standardabweichung σ = 4. Duane erzielt bei dieser Prüfung eine Punktzahl von 84.

Die Ergebnisse einer anderen College-Prüfung sind normalverteilt mit dem Mittelwert μ = 85 und der Standardabweichung σ = 8. Debbie erhält bei dieser Prüfung eine 90.

Wer hat im Vergleich zu seiner eigenen Verteilung der Prüfungsergebnisse die besten Ergebnisse bei seiner Prüfung erzielt?

Um diese Frage zu beantworten, können wir den Z-Score der Prüfungsergebnisse jeder Person berechnen:

Duanes z-Score = (x – μ) / σ = (84 – 80) / 4 = 4 / 4 = 1

Debbies Z-Score = (x – μ) / σ = (90 – 85) / 8 = 5/8 = 0,625

Obwohl Debbie eine höhere Punktzahl erzielte, ist Duanes Punktzahl im Vergleich zur Verteilung seiner speziellen Prüfung tatsächlich höher.

Um dies zu verstehen, hilft es, sich die Situation vorzustellen. Hier ist Duanes Punktzahl im Vergleich zu seiner speziellen Prüfungsaufschlüsselung:

Und hier ist Debbies Ergebnis aus ihrer Prüfungsaufschlüsselung:

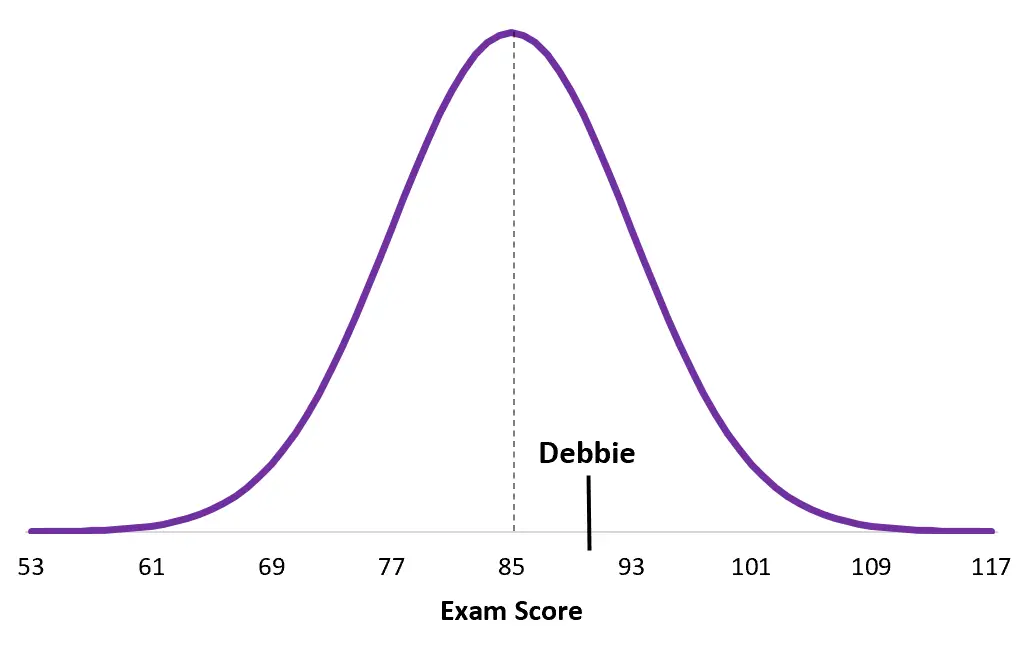
Beachten Sie, wie viel näher Debbies Wert am Bevölkerungsdurchschnitt liegt als der von Duane. Obwohl sie insgesamt eine höhere Punktzahl hat, ist ihr Z-Score niedriger, einfach weil die durchschnittliche Punktzahl bei ihrer jeweiligen Prüfung höher ist.

Dieses Beispiel veranschaulicht, warum Z-Scores für den Vergleich von Datenwerten aus verschiedenen Verteilungen so nützlich sind: Z-Scores berücksichtigen den Mittelwert und die Standardabweichungen von Verteilungen, was es uns ermöglicht, Datenwerte aus verschiedenen Verteilungen zu vergleichen und zu sehen, was der Fall ist höher im Vergleich zu ihren eigenen Ausschüttungen.

Zusätzliche Ressourcen

Z-Score-Rechner
Vergleichen Sie den Z-Score-Rechner