Stichprobenverteilung des anteils

Von Dr. Benjamin Anderson August 3, 2023 Statistiken Keine Kommentare

In diesem Artikel wird erläutert, was die Stichprobenverteilung des Anteils in der Statistik ist. Ebenso finden Sie die Proportional-Stichprobenverteilungsformel und zusätzlich eine Schritt-für-Schritt gelöste Übung.

Wie ist die Stichprobenverteilung des Anteils?

Die Stichprobenverteilung der Anteile (oder Stichprobenverteilung der Anteile ) ist die Verteilung, die sich aus der Berechnung des Anteils jeder möglichen Stichprobe aus einer Grundgesamtheit ergibt. Das heißt, die Stichprobenanteile aller möglichen Stichproben aus einer Grundgesamtheit bilden die Stichprobenverteilung des Anteils.

Mit anderen Worten: Die Stichprobenverteilung des Anteils wird ermittelt, indem alle Stichproben untersucht werden, die aus einer Grundgesamtheit ausgewählt werden können, und der Stichprobenanteil jeder Stichprobe abgeleitet wird. Somit stellt die Menge der berechneten Stichprobenanteile die Stichprobenverteilung des Anteils dar.

Falls Sie sich fragen, wozu die Stichprobenverteilung des Anteils dient: In der Statistik wird sie verwendet, um die Wahrscheinlichkeit zu berechnen, bei der Analyse einer einzelnen Stichprobe den Wert des Bevölkerungsanteils zu erreichen.

➤ Siehe: Stichprobenverteilung des Mittelwerts

Proportionale Stichprobenverteilungsformel

Wenn wir einen Teil einer Stichprobe untersuchen, analysieren wir tatsächlich Erfolgsfälle. Daher folgt die Zufallsvariable in der Studie einer binomialen Wahrscheinlichkeitsverteilung .

Nach dem zentralen Grenzwertsatz können wir für große Größen (n>30) eine Binomialverteilung näher an eine Normalverteilung bringen. Daher nähert sich die Stichprobenverteilung des Anteils einer Normalverteilung mit den folgenden Parametern an:

$\begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}$

Gold

$p$

ist die Erfolgswahrscheinlichkeit und

$q$

ist die Wahrscheinlichkeit des Scheiterns

$q=1-p$

Hinweis: Eine Binomialverteilung kann nur dann einer Normalverteilung angenähert werden, wenn

$n>30″ title=“Rendered by QuickLaTeX.com“ height=“14″ width=“52″ style=“vertical-align: -2px;“> , <p class=$ $np\ge 5$

Und

$nq\ge 5$

➤ Siehe: Beispiele für Normalverteilungen

Da die Stichprobenverteilung des Anteils einer Normalverteilung angenähert werden kann, lautet die Formel zur Berechnung einer Wahrscheinlichkeit im Zusammenhang mit dem Anteil einer Stichprobe daher:

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}$

Gold:

$\widehat{p}$

ist der Stichprobenanteil.
$p$

ist der Anteil der Bevölkerung.
$q$

ist die Ausfallwahrscheinlichkeit der Bevölkerung,

$q=1-p$

.
$n$

ist die Stichprobengröße.
$Z$

ist eine durch die Standardnormalverteilung N(0,1) definierte Variable.

Konkretes Beispiel für eine proportionale Stichprobenverteilung

Nachdem wir die Definition von Proportion Sampling Distribution und die dazugehörigen Formeln kennengelernt haben, finden Sie unten ein Schritt-für-Schritt-Lösungsbeispiel, um das Konzept vollständig zu verstehen.

Ein Industrieunternehmen kauft Teilechargen von einer Fabrik, die behauptet, die Teile mit nur 3 % fehlerhaften Teilen herzustellen. Um dies zu überprüfen, beschließt das Unternehmen, eine Bestellung von 500 Teilen zu analysieren. Wie groß ist die Wahrscheinlichkeit, in der Stichprobe mehr als 5 % fehlerhafte Teile zu finden?

In diesem Fall beträgt der Anteil der Bevölkerung, den wir untersuchen möchten, 0,03, sodass der Parameter q 0,97 entspricht.

$\begin{array}{c}p=0,03\\[2ex]q=1-p=0,97\end{array}$

Um also die Wahrscheinlichkeit zu ermitteln, mit der sie uns fragen, müssen wir die entsprechende Statistik berechnen, indem wir die Formel anwenden, die wir im vorherigen Abschnitt gesehen haben:

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}=\cfrac{0,05-0,03}{\displaystyle\sqrt{\frac{0,03\cdot 0,97}{500}}}=2,62$

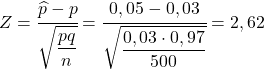
Somit entspricht die Wahrscheinlichkeit, mehr als 5 % fehlerhafte Teile zu erhalten, der folgenden Wahrscheinlichkeit:

$P\left[\widehat{p}>0,05\right]=P[Z>2,62]=1-P[Z\leq 2,62]“ title=“Rendered by QuickLaTeX.com“ height=“19″ width=“360″ style=“vertical-align: -5px;“> Schließlich suchen wir in der <a href=$ Z-Verteilungstabelle nach der Wahrscheinlichkeit von P[Z≤2,62] und berechnen die Wahrscheinlichkeit, mit der das Problem uns fragt:

$\begin{array}{l}P\left[\widehat{p}>0,05\right]=\\[2ex]=P[Z>2,62]=\\[2ex]=1-P[Z\leq 2,62]=\\[2ex]=1-0,9956=\\[2ex]=0,0044\end{array}“ title=“Rendered by QuickLaTeX.com“ height=“167″ width=“162″ style=“vertical-align: 0px;“> Zusammenfassend liegt die Wahrscheinlichkeit, in der analysierten Probe mehr als 5 % fehlerhafte Teile zu finden, bei 0,44 %. </div>  <div class=$

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen

Wie ist die Stichprobenverteilung des Anteils?

Proportionale Stichprobenverteilungsformel

Konkretes Beispiel für eine proportionale Stichprobenverteilung

Über den Autor

Dr. Benjamin Anderson

Einen Kommentar hinzufügen