Studentische t-verteilung
In diesem Artikel wird erläutert, was die Student-t-Verteilung ist und wofür sie verwendet wird. Darüber hinaus wird das Diagramm der Student-t-Verteilung gezeigt und welche Merkmale diese Art von Wahrscheinlichkeitsverteilung aufweist.
Wie ist die Studentenverteilung?
Die Student-t-Verteilung ist eine in der Statistik weit verbreitete Wahrscheinlichkeitsverteilung. Insbesondere wird die Student-t-Verteilung im Student-t-Test verwendet, um die Differenz zwischen den Mittelwerten zweier Stichproben zu bestimmen und Konfidenzintervalle festzulegen.
Die Student-t-Verteilung wurde 1908 vom Statistiker William Sealy Gosset unter dem Pseudonym „Student“ entwickelt.
Die Student-t-Verteilung wird durch die Anzahl der Freiheitsgrade definiert, die durch Subtrahieren einer Einheit von der Gesamtzahl der Beobachtungen ermittelt wird. Daher lautet die Formel zur Bestimmung der Freiheitsgrade der Student-t-Verteilung ν=n-1 .
![\begin{array}{c}\nu=n-1\\[2ex]X\sim t_\nu\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-1c805dc2d6ca050feb70dad99de53402_l3.png "Rendered by QuickLaTeX.com")
T-Verteilungsdiagramm des Schülers
Nachdem wir nun die Definition der Student-t-Verteilung kennen, wollen wir uns ansehen, wie ihr Diagramm aussieht. Unten sehen Sie grafisch einige Beispiele für Student-t-Verteilungen mit unterschiedlichen Freiheitsgraden.
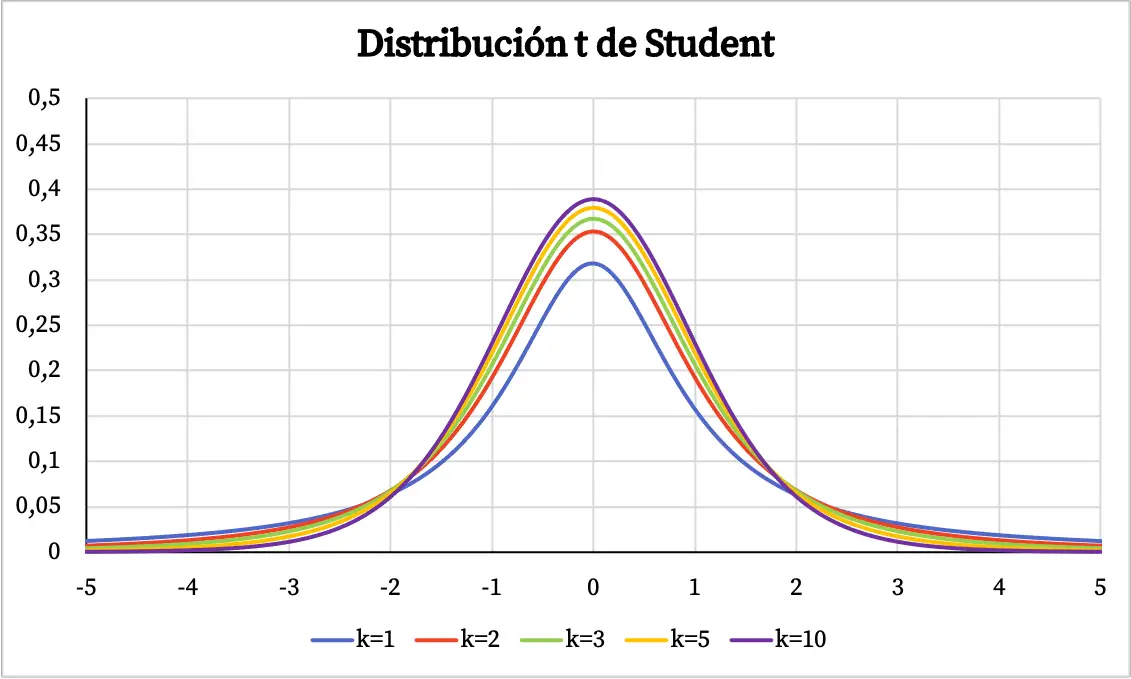
Aus dem Diagramm der Student-t-Verteilung lassen sich folgende Eigenschaften ableiten:
- Die Student-t-Verteilung ist symmetrisch, zentriert bei 0 und hat eine Glockenform.
- Die Student-t-Verteilung ist stärker gestreut als die Normalverteilung, das heißt, die Kurve der Student-t-Verteilung ist breiter.
- Je mehr Freiheitsgrade die Student-t-Verteilung hat, desto geringer ist ihre Streuung.
In der obigen Grafik wurde die Dichtefunktion der Student-t-Verteilung gegen ihre Freiheitsgrade aufgetragen. Unten können Sie jedoch sehen, wie die kumulative Wahrscheinlichkeitsfunktion der Student-t-Verteilung variiert:
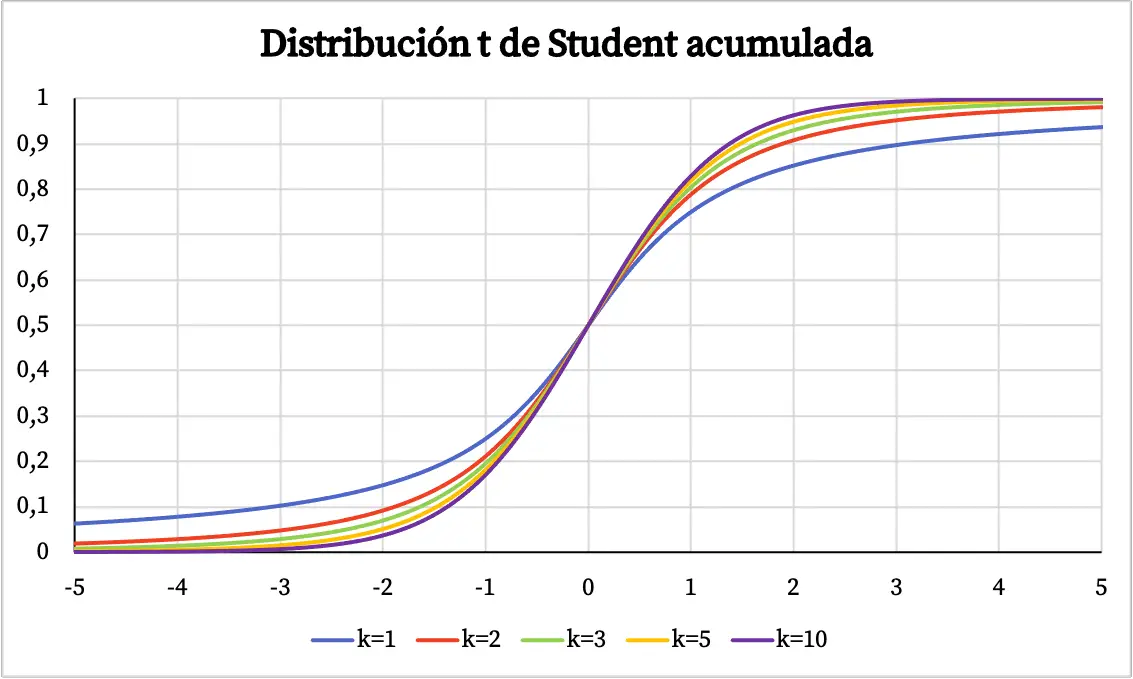
Merkmale der Student-t-Verteilung
Nachfolgend sind die wichtigsten Merkmale der Student-t-Verteilung dargestellt.
- Der Definitionsbereich der Student-t-Verteilung besteht aus reellen Zahlen.
- Für Student-t-Verteilungen mit mehr als einem Freiheitsgrad ist der Mittelwert der Verteilung gleich 0.
![\begin{array}{c}X\sim t_\nu\\[2ex] E[X]=0 \qquad \text{para }\nu>1\end{array} “ title=“Rendered by QuickLaTeX.com“ height=“55″ width=“190″ style=“vertical-align: 0px;“></p>
</p>
<ul>
<li> Die Varianz der Student-t-Verteilung kann mit dem folgenden Ausdruck berechnet werden:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-d4fed5eadcaa1162752aeedb7f8a0906_l3.png)
![\begin{array}{c}X\sim t_\nu\\[2ex] Var(X)=\cfrac{\nu}{\nu-2} \qquad \text{para }\nu>2\end{array} “ title=“Rendered by QuickLaTeX.com“ height=“75″ width=“245″ style=“vertical-align: 0px;“></p>
</p>
<ul>
<li> Der Median und Modus der Student-t-Verteilung sind unabhängig von der Anzahl der Freiheitsgrade immer 0.</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-bfdcbc8a5f071a61e091b0ef6f686a16_l3.png)
![\begin{array}{c}Me=0\\[2ex]Mo=0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-8d90790fce0c987648c0b30216c82214_l3.png "Rendered by QuickLaTeX.com")
- Die Dichtefunktion der Student-t-Verteilung wird durch die folgende Formel definiert:
![\displaystyle P[X=x]=\frac{\Gamma((\nu+1)/2)} {\sqrt{\nu\pi}\,\Gamma(\nu/2)} (1+x^2/\nu)^{-(\nu+1)/2}](https://statorials.org/wp-content/ql-cache/quicklatex.com-8c0f1e97a8e407e8b9e2b00ba93aee0e_l3.png "Rendered by QuickLaTeX.com")
- Die kumulative Wahrscheinlichkeitsverteilungsfunktion der Student-t-Verteilung wird durch die folgende Formel definiert:
![\displaystyle P[X\leq x]=\frac{1}{2} + x \Gamma \left( \frac{\nu+1}{2} \right) \cdot\frac{\,_2F_1 \left ( \frac{1}{2},\frac{\nu+1}{2};\frac{3}{2};-\frac{x^2}{\nu} \right)}{\sqrt{\pi\nu}\,\Gamma \left(\frac{\nu}{2}\right)}](https://statorials.org/wp-content/ql-cache/quicklatex.com-da1e3bdf2d87c3a7dcc89c236958dcec_l3.png "Rendered by QuickLaTeX.com")
- Für Student-t-Verteilungen mit Freiheitsgraden größer als 3 ist der Asymmetriekoeffizient Null, da es sich um eine symmetrische Verteilung handelt.
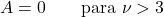
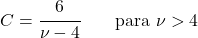Anwendungen der Student-t-Verteilung
Die Student-t-Verteilung ist eine in der Statistik weit verbreitete Wahrscheinlichkeitsverteilung. Tatsächlich gibt es sogar den Student-t-Test, der zum Testen von Hypothesen und Konfidenzintervallen verwendet wird.
Somit ermöglicht uns die Student-t-Verteilung, die Differenz zwischen den Mittelwerten zweier Stichproben zu analysieren, genauer gesagt, sie wird verwendet, um zu bestimmen, ob zwei Stichproben signifikant unterschiedliche Mittelwerte aufweisen. In ähnlicher Weise wird der Student-t-Test verwendet, um herauszufinden, ob die aus einer linearen Regressionsanalyse erhaltene Linie eine Steigung aufweist oder nicht.
Kurz gesagt, Anwendungen der Student-t-Verteilung basieren auf der Analyse von Datensätzen, die theoretisch einer Normalverteilung folgen, aber die Gesamtzahl der Beobachtungen ist zu gering, um diese Art von Verteilung zu verwenden.
Über den Autor
Dr. Benjamin Anderson
Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen