Snedecor f-verteilung

Von August 4, 2023 Wahrscheinlichkeit Keine Kommentare

In diesem Artikel wird erklärt, was die Snedecor F-Distribution ist und wofür sie verwendet wird. Darüber hinaus können Sie das Snedecor F-Verteilungsdiagramm und seine statistischen Eigenschaften sehen.

Was ist die Snedecor F-Verteilung?

Die Snedecor-F-Verteilung , auch Fisher-Snedecor-F-Verteilung oder einfach F-Verteilung genannt, ist eine kontinuierliche Wahrscheinlichkeitsverteilung, die bei statistischen Inferenzen, insbesondere bei der Varianzanalyse, verwendet wird.

Eine der Eigenschaften der Snedecor-F-Verteilung besteht darin, dass sie durch den Wert zweier reeller Parameter m und n definiert wird, die ihre Freiheitsgrade angeben. Daher ist das Symbol für die Snedecor-Verteilung F F m,n , wobei m und n die Parameter sind, die die Verteilung definieren.

F_{m,n}\qquad m,n>0″ title=“Rendered by QuickLaTeX.com“ height=“18″ width=“139″ style=“vertical-align: -6px;“></p> </p> <p> Mathematisch gesehen ist die Snedecor-F-Verteilung gleich dem Quotienten zwischen einer Chi-Quadrat-Verteilung und ihren Freiheitsgraden geteilt durch den Quotienten zwischen einer anderen Chi-Quadrat-Verteilung und ihren Freiheitsgraden. Somit lautet die Formel, die die Snedecor-F-Verteilung definiert, wie folgt: </p> </p> <p class=\left.\begin{array}{c} X\sim \chi_m^2\\[2ex] Y\sim \chi_n^2\end{array}\right\}\color{orange}\bm{\longrightarrow}\color{black}\ F_{m,n}= \cfrac{X/m}{Y/n}

Die Fisher-Snedecor-F-Verteilung verdankt ihren Namen dem englischen Statistiker Ronald Fisher und dem amerikanischen Statistiker George Snedecor.

In der Statistik hat die Fisher-Snedecor-F-Verteilung verschiedene Anwendungen. Beispielsweise wird die Fisher-Snedecor-F-Verteilung verwendet, um verschiedene lineare Regressionsmodelle zu vergleichen, und diese Wahrscheinlichkeitsverteilung wird in der Varianzanalyse (ANOVA) verwendet.

Snedecor F-Verteilungsdiagramm

Nachdem wir die Definition der Snedecor-F-Verteilung gesehen haben, werden unten die Grafik ihrer Dichtefunktion und die Grafik ihrer kumulativen Wahrscheinlichkeit angezeigt.

In der folgenden Grafik sehen Sie mehrere Beispiele für Snedecor-F-Verteilungen mit unterschiedlichen Freiheitsgraden.

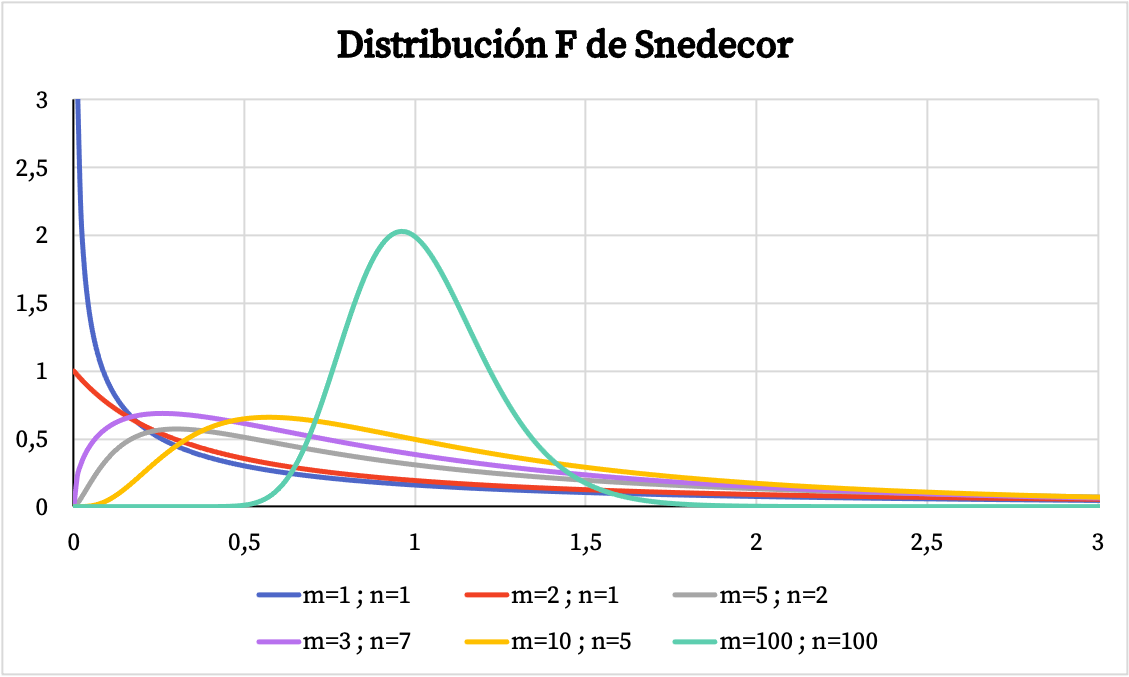
Snedecor F-Verteilungsdiagramm

Andererseits können Sie in der folgenden Grafik sehen, wie die Grafik der kumulativen Wahrscheinlichkeitsfunktion der Snedecor-F-Verteilung in Abhängigkeit von ihren charakteristischen Werten variiert.

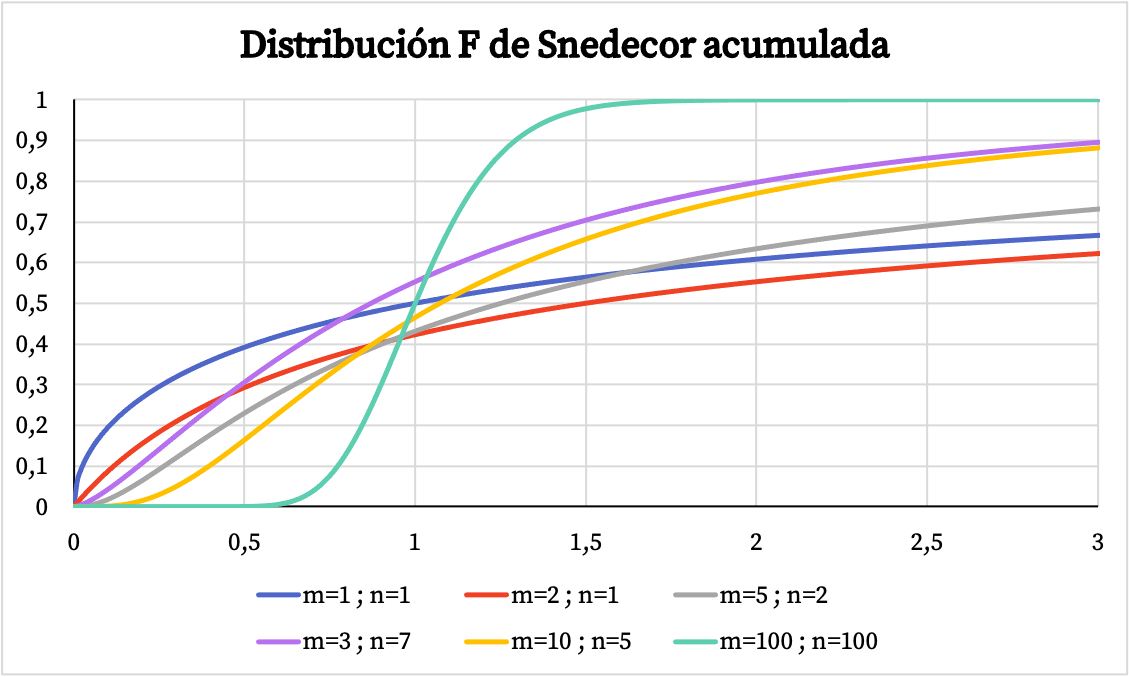
kumulative Wahrscheinlichkeit der Snedecor-F-Verteilung

Merkmale der Snedecor F-Verteilung

Abschließend werden in diesem Abschnitt die wichtigsten Merkmale der Snedecor F-Verteilung vorgestellt.

  • Die Freiheitsgrade der Snedecor F-Verteilung, m und n , sind zwei Parameter, die die Form der Verteilung definieren. Diese charakteristischen Werte der Snedecor-F-Verteilung sind positive ganze Zahlen.

\begin{array}{c}m,n \in \mathbb{Z}\\[2ex] m,n>0\end{array}“ title=“Rendered by QuickLaTeX.com“ height=“54″ width=“68″ style=“vertical-align: 0px;“></p> </p> <ul> <li> Der Definitionsbereich der Snedecor-F-Verteilung besteht aus allen reellen Zahlen größer oder gleich Null.</li> </ul> <p class=x\in [0,+\infty)

  • Für Werte von n größer als 2 ist der Mittelwert der Snedecor-F-Verteilung gleich n bei der Subtraktion von n minus 2.

\begin{array}{c}X\sim F_{m,n}\\[2ex] E[X]=\cfrac{n}{n-2} \qquad \text{para }n>2\end{array} “ title=“Rendered by QuickLaTeX.com“ height=“75″ width=“225″ style=“vertical-align: 0px;“></p> </p> <ul> <li> Wenn der Parameter <em>n</em> größer als 2 ist, kann die Varianz der Snedecor-Verteilung F durch Anwendung der folgenden Formel berechnet werden:</li> </ul> <p class=\begin{array}{c}X\sim F_{m,n}\\[2ex] Var(X)=\cfrac{2n^2\cdot (m+n-2)}{m\cdot (n-2)^2\cdot (n-4)} \qquad \text{para }n>4\end{array} “ title=“Rendered by QuickLaTeX.com“ height=“80″ width=“366″ style=“vertical-align: 0px;“></p> </p> <ul> <li> Wenn der Parameter <em>m</em> größer als 2 ist, kann der Modus der Snedecor-Verteilung F mit dem folgenden Ausdruck berechnet werden:</li> </ul> <p class=Mo=\cfrac{m-2}{m}\cdot \cfrac{n}{n+2}\qquad \text{para }m>2″ title=“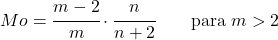Rendered by QuickLaTeX.com“ height=“40″ width=“278″ style=“vertical-align: -14px;“></p> </p> <ul> <li> Die Formel für die Dichtefunktion der Snedecor-Verteilung F lautet wie folgt:</li> </ul> <p class=\displaystyle P[X=x]=\frac{\Gamma\left(\frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\left(\frac{m}{n}\right)^{\frac{m}{2}}\cdot\frac{x^{\frac{m-2}{2}}}{\left(1+\frac{mx}{n}\right)^{\frac{m+n}{2}}}

  • Wenn eine Variable einer Snedecor-F-Verteilung mit den Freiheitsgraden m und n folgt, dann folgt die Umkehrung dieser Variablen einer Snedecor-F-Verteilung mit denselben Freiheitsgraden, aber geänderter Reihenfolge ihrer Werte.

X\sim F_{m,n} \ \color{orange}\bm{\longrightarrow}\color{\black} \ X^{-1}\sim F_{n,m}

  • Die Student-Verteilung hat die folgende Beziehung zur Snedecor-F-Verteilung:

X\sim t_n \ \color{orange}\bm{\longrightarrow}\color{\black} \ X^2\sim F_{1,n}

Über den Autor

Benjamin Anderson
Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen

Einen Kommentar hinzufügen

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert