Was ist die erlang-verteilung?
Die Erlang-Verteilung ist eine Wahrscheinlichkeitsverteilung, die ursprünglich von AK Erlang erstellt wurde, um die Anzahl der Telefonanrufe zu modellieren, die ein Vermittlungsstellenbetreiber gleichzeitig empfangen kann.
Die Verteilung wird in der Telefonverkehrstechnik, Warteschlangensystemen, der mathematischen Biologie und anderen Bereichen verwendet, um eine Vielzahl realer Phänomene zu modellieren.
Eigenschaften der Erlang-Verteilung
Die Erlang-Verteilung hat die folgende Wahrscheinlichkeitsdichtefunktion:
f(x; k, μ) = x k-1 e -x/μ / μ k (k-1)!
Gold:
- k: Der Formparameter. Es muss eine positive ganze Zahl sein.
- μ: Der Skalenparameter. Es muss eine positive reelle Zahl sein.
Es stellt sich heraus, dass die Erlang-Verteilung ein Sonderfall der Gamma-Verteilung ist, wenn der Formparameter k nur auf positive reelle ganze Zahlen beschränkt ist.
Beachten Sie, dass der Skalenparameter der Kehrwert des Geschwindigkeitsparameters λ ist, dh μ = 1/λ.
Die Erlang-Verteilung hat die folgenden Eigenschaften:
- Durchschnitt: k/λ
- Modus: (k-1)/λ
- Differenz: k/λ 2
- Asymmetrie: 2/√k
- Abflachung: 6/k
Die Erlang-Distribution weist die folgenden Beziehungen zu anderen Distributionen auf:
- Wenn der Formparameter k gleich 1 ist, ist die Erlang-Verteilung gleich der Exponentialverteilung .
- Wenn der Skalenparameter μ gleich 2 ist, entspricht die Erlang-Verteilung einer Chi-Quadrat-Verteilung mit 2 Freiheitsgraden.
Sehen Sie sich die Erlang-Distribution an
Die folgende Grafik zeigt die Form der Erlang-Verteilung, wenn sie verschiedene Parameter annimmt:
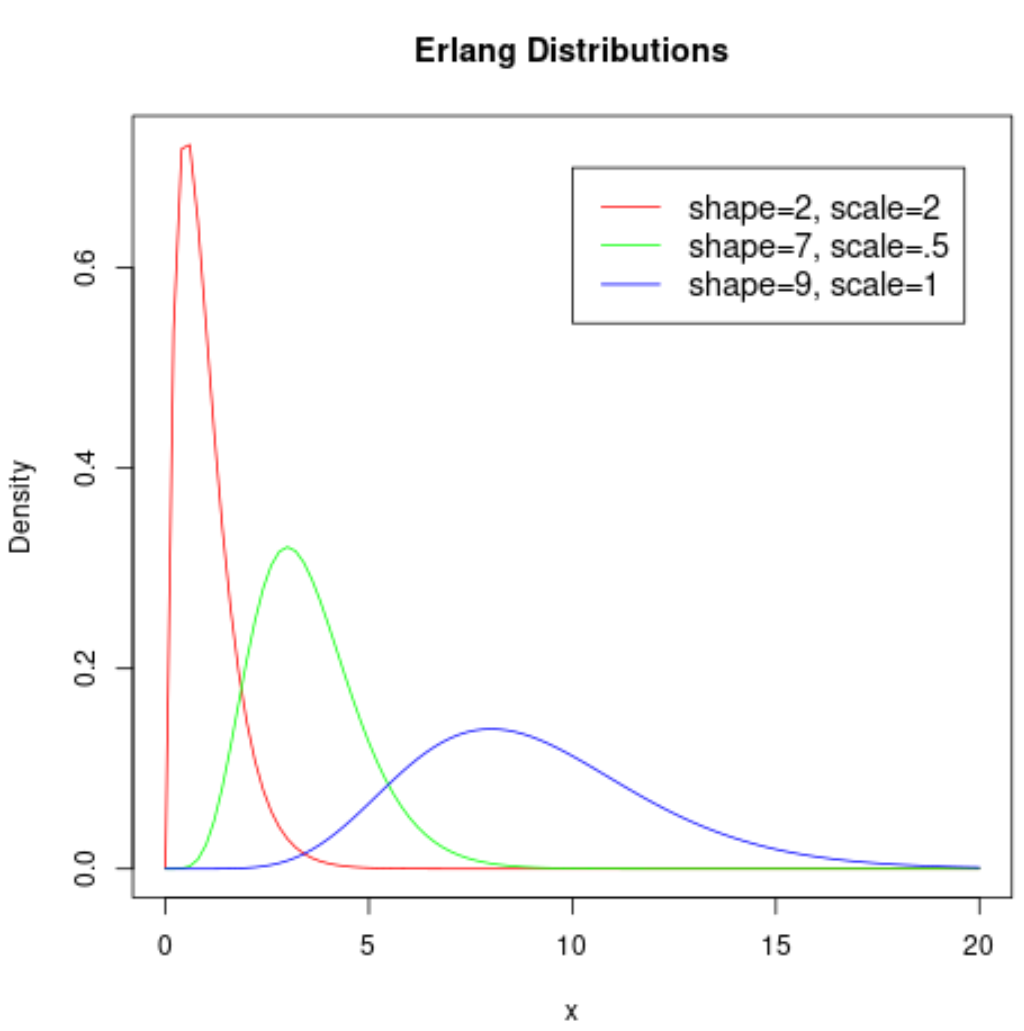
Es ist interessant zu sehen, wie stark sich die Form der Verteilung abhängig von den für die Form- und Skalenparameter verwendeten Werten ändert.
Hinweis: Den R-Code, der zum Generieren des Diagramms der Erlang-Verteilungen verwendet wird, finden Sie hier .
Anwendungsfall
Die Erlang-Distribution wird in verschiedenen realen Kontexten verwendet, darunter:
1. Callcenter
Die Erlang-Verteilung wird verwendet, um die Zeit zwischen eingehenden Anrufen in einem Callcenter sowie die erwartete Anzahl von Anrufen zu modellieren.
Auf diese Weise können Callcenter wissen, wie hoch ihre Personalkapazität zu verschiedenen Tageszeiten sein sollte, sodass sie eingehende Anrufe zeitnah bearbeiten können, ohne Geld durch die Beschäftigung zu vieler Mitarbeiter während einer Schicht zu verlieren. gegebene Arbeit.
2. Medizinische Parameter
Die Erlang-Verteilung wird häufig zur Modellierung der Verteilung der Zellzyklusdauer verwendet, die im medizinischen Bereich viele verschiedene Anwendungen hat.
3. Einzelhandelseinstellungen
Die Erlang-Verteilung wird von Einzelhändlern verwendet, um die Häufigkeit von Kaufverzögerungen durch Verbraucher zu modellieren.
Dies gibt Einzelhändlern und anderen Unternehmen eine Vorstellung davon, wie oft ein bestimmter Verbraucher voraussichtlich ein Produkt oder eine Dienstleistung bei ihnen kaufen wird. Dies hilft Unternehmen, den Lagerbestand zu kontrollieren und Personal zu rekrutieren.
Zusätzliche Ressourcen
Eine Einführung in die Normalverteilung
Eine Einführung in die Binomialverteilung
Eine Einführung in die Poisson-Verteilung
Über den Autor
Dr. Benjamin Anderson
Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen