Verteilungsfunktion
In diesem Artikel finden Sie die Erklärung der Verteilungsfunktion, wie ihre Werte berechnet werden und ein reales Beispiel der Verteilungsfunktion. Darüber hinaus können Sie die Unterschiede zwischen einer Verteilungsfunktion und einer Dichtefunktion erkennen.
Was ist die Verteilungsfunktion?
Die Verteilungsfunktion , auch kumulative Verteilungsfunktion genannt, ist eine mathematische Funktion, die die kumulative Wahrscheinlichkeit einer Verteilung angibt. Das heißt, das Bild der Verteilungsfunktion für jeden Wert ist gleich der Wahrscheinlichkeit, dass die Variable diesen Wert oder einen niedrigeren Wert annimmt.
Die kumulative Verteilungsfunktion kann auch mit dem Akronym FDA bezeichnet werden, obwohl das übliche Symbol das große F ist.
Die Verteilungsfunktion wird daher durch die folgende Formel definiert:
![]()
So berechnen Sie die Verteilungsfunktion
Anschließend erklären wir, wie der Wert der Verteilungsfunktion abhängig davon berechnet wird, ob die Wahrscheinlichkeitsverteilung diskret oder kontinuierlich ist.
Diskrete Box
Wenn die Zufallsvariable diskret ist, ist die kumulative Verteilungsfunktion gleich der Summe der Wahrscheinlichkeiten aller Werte gleich oder kleiner als x .
![]()
Gold
![]()
ist die Wahrscheinlichkeitsfunktion, die der diskreten Variablen zugeordnet ist.
Fortlaufender Fall
Wenn die Zufallsvariable stetig ist, entspricht die kumulative Verteilungsfunktion dem Integral der Dichtefunktion von minus unendlich bis zum betreffenden Wert.
![]()
Gold
![]()
ist die Dichtefunktion, die der kontinuierlichen Variablen zugeordnet ist.
Beispiel für eine Verteilungsfunktion
Nachdem wir nun die Definition der Verteilungsfunktion kennen, schauen wir uns ein praktisches Schritt-für-Schritt-Beispiel an, um zu lernen, wie man einen Verteilungsfunktionswert berechnet.
- Berechnen Sie die Verteilungsfunktion für das Zufallsexperiment, bei dem eine Münze viermal geworfen wird.
Um die Aufgabe zu lösen, müssen Sie zunächst alle Wahrscheinlichkeiten berechnen, die mit der Anzahl der Köpfe bei den vier Münzwürfen verbunden sind:

Da es sich also um eine diskrete Variable handelt, reicht es zur Bestimmung der Bilder der Verteilungsfunktion aus, die Wahrscheinlichkeiten zum Wert der betreffenden Variablen zu addieren:
![Rendered by QuickLaTeX.com \begin{array}{l}F(X\leq 0)=f(0)=0,0625\\[4ex]\begin{aligned}F(X\leq 1)& =f(0)+f(1)\\[1.1ex] & =0,0625+0,25=0,3125\end{aligned}\\[6ex]\begin{aligned}F(X\leq 2)& =f(0)+f(1)+f(2)\\[1.1ex] & =0,0625+0,25+0,375=0,6875\end{aligned}\\[6ex]\begin{aligned}F(X\leq 3)& =f(0)+f(1)+f(2)+f(3)\\[1.1ex] & =0,0625+0,25+0,375+0,25=0,9375\end{aligned}\\[6ex]\begin{aligned}F(X\leq 4)& =f(0)+f(1)+f(2)+f(3)+f(4)\\[1.1ex] & =0,0625+0,25+0,375+0,25+0,0625=1\end{aligned}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-63c3574be5cdcf6de8b54f910c01e35e_l3.png)
Somit sind die Werte der Verteilungsfunktion des Kopfdrehens durch Werfen von vier unabhängigen Münzen wie folgt:
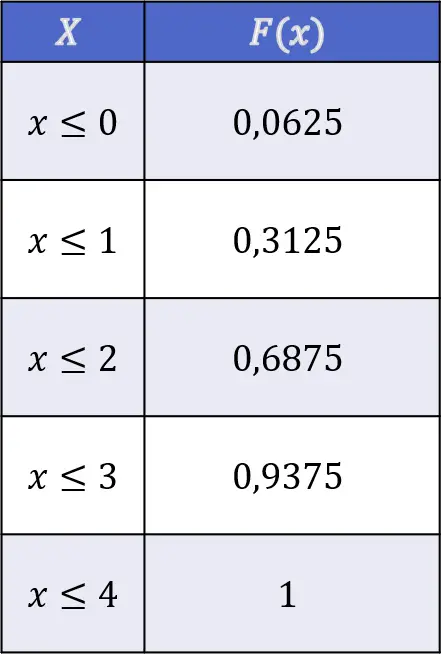
Eigenschaften der Verteilungsfunktion
Unabhängig von der Art der Variablen hat die Verteilungsfunktion immer die folgenden Eigenschaften:
- Der Wert der kumulativen Verteilungsfunktion liegt zwischen 0 und 1 (einschließlich).
![]()
- Der Grenzwert einer Verteilungsfunktion, wenn x gegen Unendlich geht, ist gleich 1.
![]()
- Andererseits ist der Grenzwert einer Verteilungsfunktion Null, wenn sich x minus Unendlich nähert.
![]()
- Aufgrund ihrer Eigenschaften ist die Verteilungsfunktion monoton und nicht abnehmend.
![]()
- Darüber hinaus, wenn
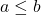
die folgenden Gleichungen sind erfüllt.
*** QuickLaTeX cannot compile formula:
\begin{array}{l}P(X < a) = F(a^-)\\[2ex] P(X>a)=1-F(a)\\[2ex]P(X \ge a )=1-F(a^-)\\[2ex]P(a<ul><li> Finally, if the statistical variable is continuous, the following equality is satisfied: </li></ul>[latex ]\begin{array}{l}P(a \le X < b) = \displaystyle\int_{a}^{b}f(x)\,dx = F(b)- F(a)\end{array}
*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ... the statistical variable is continuous, the
Please use \mathaccent for accents in math mode.
leading text: ...iable statistic is continuous, equality
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Verteilungsfunktion und Dichtefunktion
Abschließend werden wir sehen, was der Unterschied zwischen der Verteilungsfunktion und der Dichtefunktion ist, da diese beiden statistischen Begriffe oft verwechselt werden.
Der Unterschied zwischen der Verteilungsfunktion und der Dichtefunktion besteht in der Art der Wahrscheinlichkeit, die sie definieren. Die Dichtefunktion beschreibt die Wahrscheinlichkeit, dass die Variable einen bestimmten Wert annimmt, während die Verteilungsfunktion die kumulative Wahrscheinlichkeit der Variablen beschreibt.
Das heißt, die Verteilungsfunktion wird verwendet, um die Wahrscheinlichkeit zu berechnen, dass die Variable gleich oder kleiner als ein bestimmter Wert ist.
Beachten Sie, dass sich die Dichtefunktion nur auf kontinuierliche Variablen bezieht, sodass diese Unterscheidung nur dann sinnvoll ist, wenn die untersuchte Variable kontinuierlich ist.
Beachten Sie, wie sich die grafische Darstellung der Verteilungsfunktion im Vergleich zur Dichtefunktion einer Variablen ändert, die einer Normalverteilung mit einem Mittelwert von 1 und einer Standardabweichung von 0,5 folgt:

Weitere Informationen zur Dichtefunktion finden Sie im folgenden Artikel: