Was ist ein vorhersagefehler in der statistik? (definition & beispiele)

In der Statistik bezeichnet der Vorhersagefehler die Differenz zwischen den von bestimmten Modellen vorhergesagten Werten und den tatsächlichen Werten.

Vorhersagefehler werden häufig in zwei Zusammenhängen verwendet:

1. Lineare Regression: Wird verwendet, um den Wert einer kontinuierlichen Antwortvariablen vorherzusagen.

Normalerweise messen wir den Vorhersagefehler eines linearen Regressionsmodells mit einer Metrik namens RMSE , die für Root Mean Square Error steht.

Es wird wie folgt berechnet:

RMSE = √ Σ(ŷ _i – y _i ) ² / n

Gold:

• Σ ist ein Symbol, das „Summe“ bedeutet
• ŷ _i ist der vorhergesagte Wert für die i- ^te Beobachtung
• y _i ist der beobachtete Wert für die ^i-te Beobachtung
• n ist die Stichprobengröße

2. Logistische Regression: Wird verwendet, um den Wert einer binären Antwortvariablen vorherzusagen.

Eine übliche Methode zur Messung des Vorhersagefehlers eines logistischen Regressionsmodells ist die Verwendung einer Metrik, die als Gesamtklassifizierungsfehlerrate bekannt ist.

Es wird wie folgt berechnet:

Gesamtfehlklassifizierungsrate = (# falsche Vorhersagen / # Gesamtvorhersagen)

Je niedriger der Wert der Fehlklassifizierungsrate ist, desto besser kann das Modell die Ergebnisse der Antwortvariablen vorhersagen.

Die folgenden Beispiele zeigen, wie der Vorhersagefehler für ein lineares Regressionsmodell und ein logistisches Regressionsmodell in der Praxis berechnet wird.

Beispiel 1: Berechnung des Vorhersagefehlers in der linearen Regression

Angenommen, wir verwenden ein Regressionsmodell, um vorherzusagen, wie viele Punkte 10 Spieler in einem Basketballspiel erzielen werden.

Die folgende Tabelle zeigt die vom Modell vorhergesagten Punkte im Vergleich zu den tatsächlich von den Spielern erzielten Punkten:

Wir würden den quadratischen Mittelwertfehler (RMSE) wie folgt berechnen:

• RMSE = √ Σ(ŷ _i – y _i ) ² / n
• RMSE = √(((14-12) ² +(15-15) ² +(18-20) ² +(19-16) ² +(25-20) ² +(18-19) ² +(12- 16) ² +(12-20) ² +(15-16) ² +(22-16) ² ) / 10)
• RMSE = 4

Der mittlere quadratische Fehler beträgt 4. Dies sagt uns, dass die durchschnittliche Abweichung zwischen den vorhergesagten erzielten Punkten und den tatsächlich erzielten Punkten 4 beträgt.

Verwandt: Was gilt als guter RMSE-Wert?

Beispiel 2: Berechnung des Vorhersagefehlers in der logistischen Regression

Angenommen, wir verwenden ein logistisches Regressionsmodell, um vorherzusagen, ob 10 College-Basketballspieler in die NBA eingezogen werden oder nicht.

Die folgende Tabelle zeigt das vorhergesagte Ergebnis für jeden Spieler im Vergleich zum tatsächlichen Ergebnis (1 = gedraftet, 0 = nicht gedraftet):

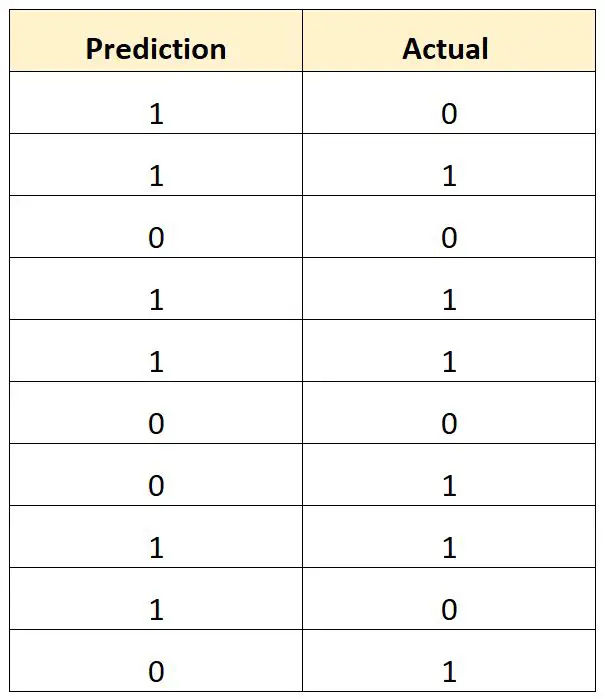
Wir würden die Gesamtfehlklassifizierungsrate wie folgt berechnen:

• Gesamtfehlklassifizierungsrate = (# falsche Vorhersagen / # Gesamtvorhersagen)
• Gesamtklassifizierungsfehlerrate = 4/10
• Gesamtfehlklassifizierungsrate = 40 %

Die Gesamtklassifizierungsfehlerquote beträgt 40 % .

Dieser Wert ist ziemlich hoch, was darauf hindeutet, dass das Modell nicht sehr gut vorhersagen kann, ob ein Spieler gedraftet wird oder nicht.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten eine Einführung in die verschiedenen Arten von Regressionsmethoden:

Einführung in die einfache lineare Regression
Einführung in die multiple lineare Regression
Einführung in die logistische Regression