Wahrscheinlichkeit vs. proportion: was ist der unterschied?

Zwei Begriffe, die Studierende in der Statistik häufig verwechseln, sind Wahrscheinlichkeit und Proportion .

Hier ist der Unterschied:

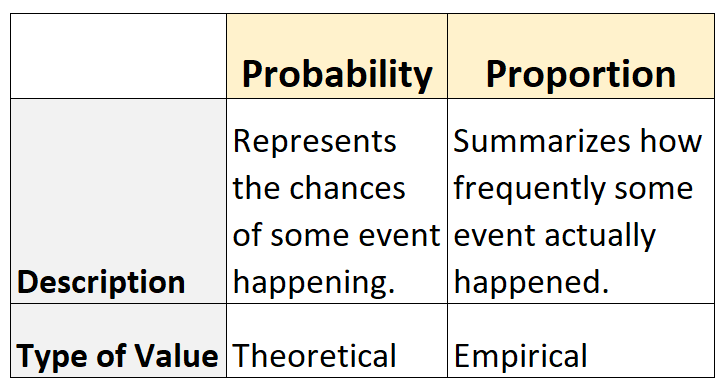
• Die Wahrscheinlichkeit stellt die Wahrscheinlichkeit dar, mit der ein Ereignis eintritt. Es ist theoretisch .
• Der Anteil fasst zusammen, wie oft ein Ereignis tatsächlich aufgetreten ist. Es ist empirisch .

Wir verwenden häufig die Wahrscheinlichkeit, um über die Wahrscheinlichkeit zu sprechen, dass ein Ereignis in der Zukunft eintritt.

Im Gegensatz dazu verwenden wir Proportionen oft, um zu beschreiben, wie oft ein Ereignis in der Vergangenheit tatsächlich stattgefunden hat.

Die folgenden Beispiele veranschaulichen die Unterschiede zwischen Wahrscheinlichkeiten und Anteilen in verschiedenen Szenarien.

Beispiel 1: Wahrscheinlichkeit versus Verhältnis beim Münzwerfen

Wenn wir eine faire Münze werfen, beträgt die Wahrscheinlichkeit , dass sie „Kopf“ ergibt, 0,5 oder 50 % .

Wenn wir jedoch eine Münze 20 Mal werfen, können wir tatsächlich zählen, wie oft sie „Kopf“ ergibt. Zum Beispiel kann es sein, dass er in 60 % der Fälle, in denen er wirft, Kopf hochgekommen ist.

Die Wahrscheinlichkeit, dass die Münze „Kopf“ landet, ist theoretisch, aber der Anteil, wie oft die Münze „Kopf“ landet, ist empirisch – wir könnten den Anteil tatsächlich zählen.

Beispiel 2: Wahrscheinlichkeit versus Anteil bei Würfelwürfen

Wenn Sie einen sechsseitigen Würfel werfen, beträgt die Wahrscheinlichkeit , dass er auf die Zahl „4“ fällt, 1/6 oder etwa 16,67 % .

Wenn wir den Würfel jedoch 10 Mal würfeln, können wir zählen, wie oft er auf der 4 gelandet ist. Beispielsweise könnte er in 20 % der Würfe auf der „4“ gelandet sein.

Die Wahrscheinlichkeit, eine „4“ zu würfeln, ist theoretisch, aber der Anteil, wie oft der Würfel auf einer „4“ landet, ist empirisch – wir könnten den Anteil tatsächlich zählen.

Beispiel 3: Wahrscheinlichkeit vs. Anteil an Spinnern

Wenn wir ein Rouletterad drehen, das in vier gleiche Teile geteilt ist – Rot, Blau, Grün und Lila –, beträgt die Wahrscheinlichkeit , dass es bei jeder Drehung auf Lila landet, 25 % .

Wenn wir das Rouletterad jedoch 100 Mal drehen, können wir zählen, wie oft es auf Lila gelandet ist. Beispielsweise landete er vielleicht bei 15 % der Drehungen auf Lila.

Die Wahrscheinlichkeit, dass das Rouletterad auf Lila landet, ist theoretisch, aber der Anteil, wie oft es auf Lila landet, ist empirisch – wir könnten den Anteil tatsächlich zählen.

Beispiel 4: Wahrscheinlichkeit versus Verhältnis bei Kartenspielen

In einem Standarddeck mit 52 Karten gibt es 4 Damen. Die Wahrscheinlichkeit , in einer Ziehung eine Königin zu wählen, beträgt also 4/52 = 7,69 % .

Wenn wir jedoch 50 Mal nach dem Zufallsprinzip ziehen (und die gezogene Karte ersetzen), können wir tatsächlich zählen, wie oft wir eine Königin ziehen. Vielleicht ziehen wir zum Beispiel in 10 % der Ziehungen eine Königin.

Die Wahrscheinlichkeit, eine Königin zu wählen, ist theoretisch, aber der Anteil, wie oft wir tatsächlich eine Königin wählen, ist empirisch – wir könnten den Anteil tatsächlich zählen.

Zusätzliche Ressourcen

Wahrscheinlichkeit vs. Wahrscheinlichkeit: Was ist der Unterschied?
Gesetz der Gesamtwahrscheinlichkeit: Definition und Beispiele