Wahrscheinlichkeitsfunktion

In diesem Artikel wird erklärt, was Wahrscheinlichkeitsfunktionen sind. So finden Sie die Bedeutung einer Wahrscheinlichkeitsfunktion, ihre Eigenschaften und ein konkretes Beispiel für die Berechnung einer Wahrscheinlichkeitsfunktion. Darüber hinaus werden die Unterschiede zwischen einer Wahrscheinlichkeitsfunktion und anderen Arten von Wahrscheinlichkeitsfunktionen dargestellt.

Was ist eine Wahrscheinlichkeitsfunktion?

Eine Wahrscheinlichkeitsfunktion , auch Wahrscheinlichkeitsmassenfunktion genannt, ist eine mathematische Funktion, die die Wahrscheinlichkeit beschreibt, mit der eine diskrete Zufallsvariable einen bestimmten Wert annimmt.

Das heißt, eine Wahrscheinlichkeitsfunktion gibt die mit einer diskreten Variablen verbundene Wahrscheinlichkeit zurück, genau gleich einem Wert zu sein.

Beispielsweise beträgt die Wahrscheinlichkeit, beim Würfeln eine beliebige Zahl zu würfeln, 1/6 (ein Würfel hat sechs Seiten), daher ist die diesem Stichprobenraum zugeordnete Wahrscheinlichkeitsfunktion für n gleich 1/6, unabhängig vom Wert.

Eigenschaften der Wahrscheinlichkeitsfunktion

Wahrscheinlichkeitsfunktionen haben die folgenden Eigenschaften:

• Wahrscheinlichkeiten können nicht negativ sein, daher ist die Wahrscheinlichkeitsfunktion für jeden Wert von x null oder positiv.

• Ebenso ist die maximale Wahrscheinlichkeit eins, was bedeutet, dass das Ereignis immer eintritt. Daher ist der Maximalwert der Wahrscheinlichkeitsfunktion gleich 1.

• Schließlich ergibt die Summe aller Werte einer Wahrscheinlichkeitsfunktion 1, da es sich um die Summe aller Wahrscheinlichkeiten im Stichprobenraum handelt.

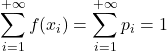
Beispiel für eine Wahrscheinlichkeitsfunktion

Nachdem wir nun die Definition und die Eigenschaften der Wahrscheinlichkeitsfunktion kennen, sehen wir uns ein Beispiel für diese Art von Wahrscheinlichkeitsfunktion an.

• Berechnen Sie die Wahrscheinlichkeiten, 0, 1, 2, 3 und 4 Mal „Kopf“ zu bekommen, indem Sie vier unabhängige Münzwürfe durchführen. Als nächstes stellen Sie die gefundene Wahrscheinlichkeitsfunktion grafisch dar.

Zunächst müssen wir die Wahrscheinlichkeiten berechnen, Kopf zu bekommen. Dazu müssen wir die möglichen Fälle durch die Gesamtzahl der Fälle dividieren. Die Berechnung aller Wahrscheinlichkeiten können Sie der folgenden Tabelle entnehmen:

Und sobald wir alle Wahrscheinlichkeiten berechnet haben, können wir die Werte der Wahrscheinlichkeitsfunktion in einem Diagramm darstellen:

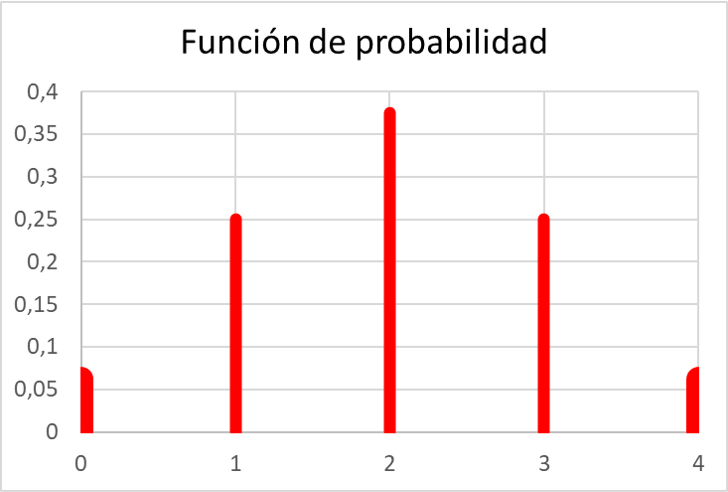
Wie Sie sehen, erfüllt die Wahrscheinlichkeitsfunktion in der Übung alle Eigenschaften von Wahrscheinlichkeitsfunktionen, da alle ihre Werte zwischen 0 und 1 liegen und darüber hinaus die Summe aller ihrer Werte gleich 1 ist.

Wahrscheinlichkeitsfunktion und Dichtefunktion

In diesem Abschnitt werden wir den Unterschied zwischen Wahrscheinlichkeitsfunktion und Dichtefunktion sehen, da es sich um zwei Arten von Wahrscheinlichkeitsfunktionen handelt, die denselben Zweck haben, aber in unterschiedlichen Fällen verwendet werden.

Der Unterschied zwischen der Wahrscheinlichkeitsfunktion und der Dichtefunktion besteht in der Art der Variablen, die die Wahrscheinlichkeiten beschreiben. Die Wahrscheinlichkeitsfunktion wird verwendet, um die Wahrscheinlichkeiten einer diskreten Variablen zu definieren, während die Dichtefunktion verwendet wird, um die Wahrscheinlichkeiten einer kontinuierlichen Variablen zu definieren.

Je nach Variable wird also eine Wahrscheinlichkeitsfunktion oder eine Dichtefunktion verwendet.

Um mehr über die Dichtefunktion zu erfahren, klicken Sie auf den folgenden Link:

Wahrscheinlichkeitsfunktion und Verteilungsfunktion

Der Unterschied zwischen einer Wahrscheinlichkeitsfunktion und einer Verteilungsfunktion besteht in der Art der Wahrscheinlichkeit, die sie definieren. Die Wahrscheinlichkeitsfunktion gibt die Wahrscheinlichkeit an, dass die Variable einen bestimmten Wert annimmt, während die Verteilungsfunktion die kumulative Wahrscheinlichkeit der Variablen beschreibt.

Daher wird die Verteilungsfunktion aus der Wahrscheinlichkeitsfunktion berechnet.

Als Beispiel sehen Sie im folgenden Link die Berechnung der Verteilungsfunktion, um bei vier Münzwürfen „Kopf“ zu erhalten, basierend auf der Wahrscheinlichkeitsfunktion aus der obigen Übung.