Wann sollten sie korrelation verwenden? (erklärung & beispiele)

Korrelation wird verwendet, um den linearen Zusammenhang zwischen zwei Variablen zu messen.

Ein Korrelationskoeffizient nimmt immer einen Wert zwischen -1 und 1 an, wobei:

• -1 zeigt eine vollkommen negative lineare Korrelation zwischen zwei Variablen an
• 0 bedeutet, dass zwischen zwei Variablen keine lineare Korrelation besteht
• 1 zeigt eine vollkommen positive lineare Korrelation zwischen zwei Variablen an

Eine von Studierenden häufig gestellte Frage lautet: Wann sollte ich Korrelation verwenden?

Die kurze Antwort: Verwenden Sie Korrelation, wenn Sie die lineare Beziehung zwischen zwei Variablen quantifizieren möchten und keine der Variablen eine Antwort- oder „Ergebnis“-Variable darstellt .

Die folgenden Beispiele veranschaulichen, wann Sie Korrelation in der Praxis verwenden sollten und wann nicht.

Beispiel 1: Wann Korrelation verwendet werden sollte

Angenommen, ein Professor möchte die lineare Beziehung zwischen den Ergebnissen von Mathematiktests und den Ergebnissen von Naturwissenschaftstests der Schüler seiner Klasse verstehen.

Schneiden beispielsweise Schüler, die in der Mathematikprüfung gut abschneiden, auch in der Naturwissenschaftsprüfung gut ab? Oder haben Schüler, die in Mathematik gute Ergebnisse erzielen, tendenziell schlechte Ergebnisse in Naturwissenschaften?

In diesem Szenario könnte er die Korrelation zwischen den Ergebnissen in Mathematikprüfungen und den Ergebnissen in naturwissenschaftlichen Prüfungen berechnen, da er lediglich die lineare Beziehung zwischen den beiden Variablen verstehen möchte und keine Variable als Antwortvariable betrachtet werden kann.

Angenommen, er berechnet den Pearson-Korrelationskoeffizienten und stellt fest, dass er r = 0,78 beträgt. Dies ist ein starker positiver Zusammenhang, was bedeutet, dass Schüler, die in Mathematik gute Leistungen erbringen, tendenziell auch in Naturwissenschaften gute Leistungen erbringen.

Beispiel 2: Wann Korrelation nicht verwendet werden sollte

Nehmen wir an, die Marketingabteilung eines Unternehmens möchte die Auswirkungen der Werbeausgaben auf den Gesamtumsatz quantifizieren.

Wie viel zusätzliche Einnahmen kann das Unternehmen beispielsweise für jeden zusätzlichen Dollar, der für Werbung ausgegeben wird, erwarten?

In diesem Szenario muss die Abteilung ein lineares Regressionsmodell verwenden, um die Beziehung zwischen Werbeausgaben und Gesamtumsatz zu quantifizieren, da die Variable „Umsatz“ die Antwortvariable ist.

Angenommen, die Abteilung wendet ein einfaches lineares Regressionsmodell an und stellt fest, dass die folgende Gleichung die Beziehung zwischen Werbeausgaben und Gesamtumsatz am besten beschreibt:

Gesamtumsatz = 145,4 + 0,34*(Werbeausgaben)

Wir würden dies so interpretieren, dass jeder zusätzliche Dollar, der für Werbung ausgegeben wird, zu einer durchschnittlichen Steigerung des Gesamtumsatzes um 0,34 Dollar führt.

Vorsichtsmaßnahmen für die Verwendung der Korrelation

Es ist wichtig zu beachten, dass Korrelation nur zur Quantifizierung der linearen Beziehung zwischen zwei Variablen verwendet werden kann.

Unter bestimmten Umständen ist ein Korrelationskoeffizient jedoch nicht in der Lage, eine Beziehung zwischen zwei Variablen, die eine nichtlineare Beziehung teilen, effektiv zu erfassen.

Angenommen, wir erstellen das folgende Streudiagramm, um die Beziehung zwischen zwei Variablen zu visualisieren:

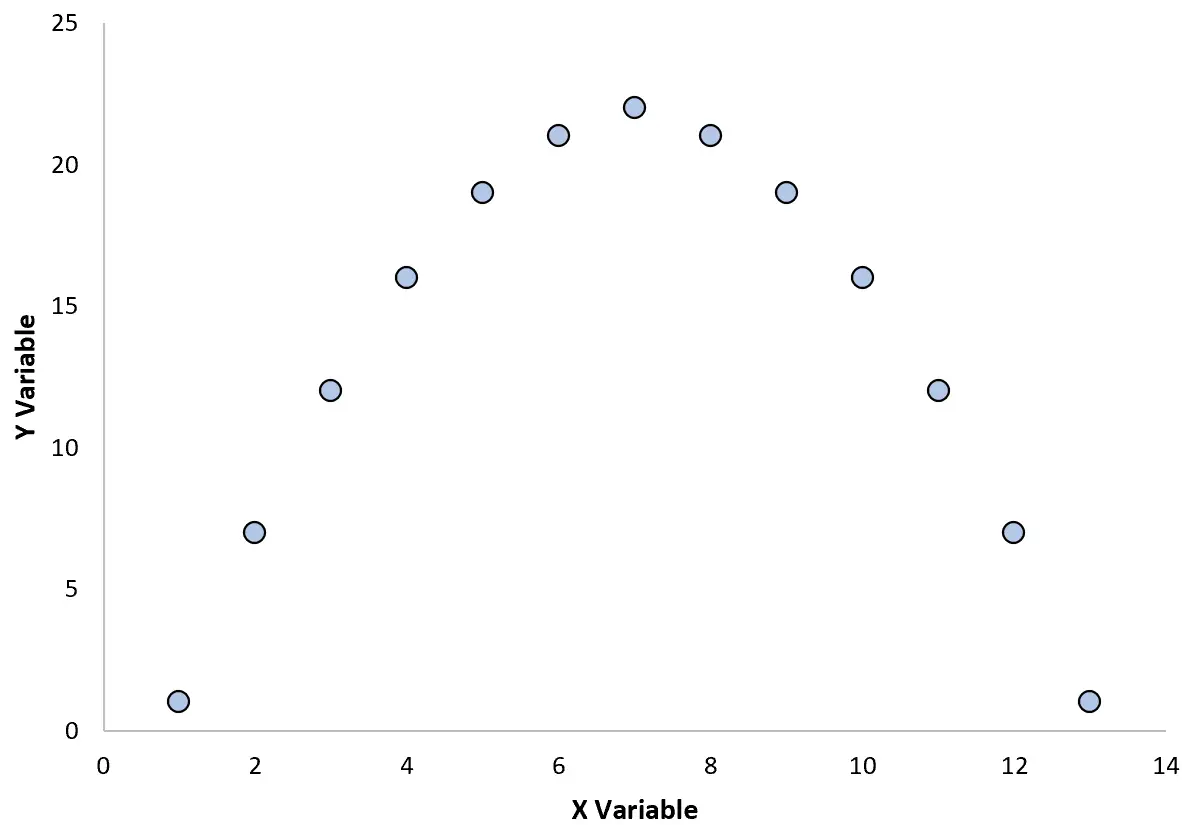
Wenn wir den Korrelationskoeffizienten zwischen diesen beiden Variablen berechnen, ergibt sich r = 0. Das bedeutet, dass zwischen den beiden Variablen kein linearer Zusammenhang besteht.

Aus der Grafik können wir jedoch erkennen, dass zwischen den beiden Variablen tatsächlich eine Beziehung besteht – es handelt sich einfach um eine quadratische Beziehung und nicht um eine lineare Beziehung.

Denken Sie also bei der Berechnung der Korrelation zwischen zwei Variablen daran, dass es auch nützlich sein kann, ein Streudiagramm zu erstellen, um die Beziehung zwischen den Variablen zu visualisieren.

Auch wenn zwischen zwei Variablen keine lineare Beziehung besteht, ist es möglich, dass zwischen ihnen eine nichtlineare Beziehung besteht, die in einem Streudiagramm sichtbar wird.

Zusätzliche Ressourcen

In den folgenden Tutorials wird ausführlicher erläutert, wie Korrelation unter verschiedenen Umständen verwendet wird:

6 reale Beispiele für Korrelationen
Was gilt als „starke“ Korrelation?
Korrelation vs. Assoziation: Was ist der Unterschied?
Korrelation vs. Regression: Was ist der Unterschied?