Wann sollten sie die polynomielle regression verwenden?

Die polynomielle Regression ist eine Technik, mit der wir ein Regressionsmodell anpassen können, wenn die Beziehung zwischen der/den Prädiktorvariablen(n) und der Antwortvariablen nichtlinear ist.

Ein polynomiales Regressionsmodell hat die folgende Form:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

In der Praxis gibt es drei einfache Möglichkeiten, um zu bestimmen, ob Sie eine polynomiale Regression oder ein einfacheres Modell wie die lineare Regression verwenden sollten.

1. Erstellen Sie ein Streudiagramm der Prädiktorvariablen und der Antwortvariablen

Der einfachste Weg, um zu bestimmen, ob Sie die polynomielle Regression verwenden sollten, besteht darin, ein einfaches Streudiagramm der Prädiktorvariablen und der Antwortvariablen zu erstellen.

Nehmen wir zum Beispiel an, wir möchten die Prädiktorvariable „Studienstunden“ verwenden, um die Note vorherzusagen, die ein Student bei einer Abschlussprüfung erhalten wird.

Bevor wir ein Regressionsmodell anpassen, können wir zunächst ein Streudiagramm der gelernten Stunden im Vergleich zu den Prüfungsergebnissen erstellen. Angenommen, unser Streudiagramm sieht so aus:

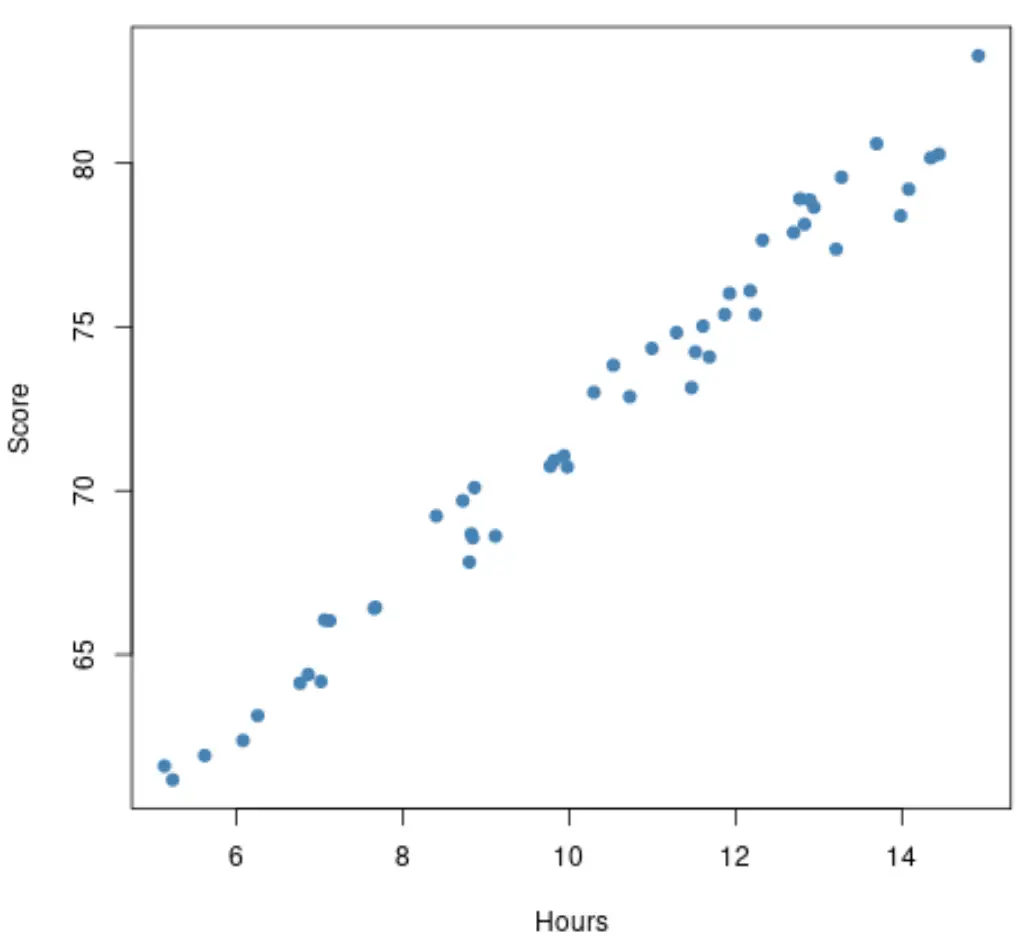
Die Beziehung zwischen den Lernstunden und den Prüfungsergebnissen scheint linear zu sein, daher wäre es sinnvoll, ein einfaches lineares Regressionsmodell an diesen Datensatz anzupassen.

Nehmen wir jedoch an, dass das Streudiagramm tatsächlich wie folgt aussieht:

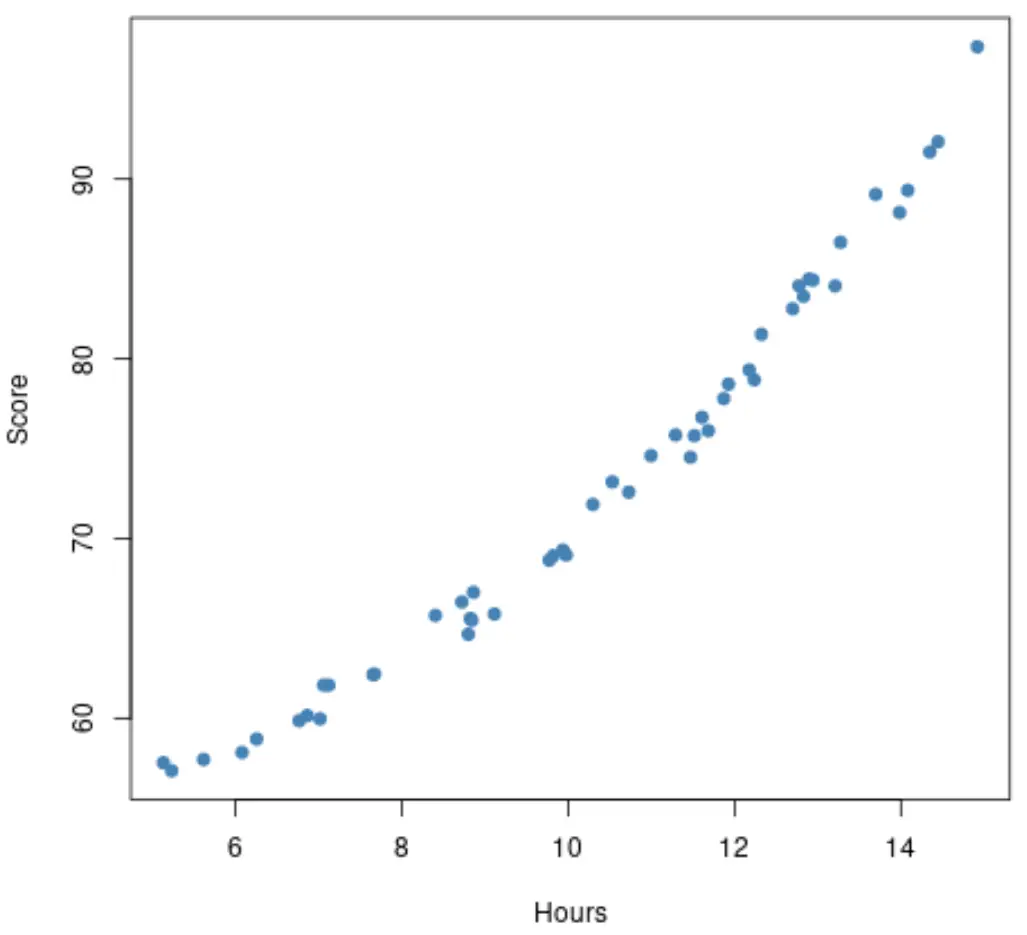
Diese Beziehung scheint etwas nichtlinearer zu sein, was uns zeigt, dass es sinnvoll sein könnte, stattdessen ein polynomiales Regressionsmodell anzupassen.

2. Erstellen Sie ein Diagramm mit angepassten Werten und Restwerten

Eine andere Möglichkeit zu bestimmen, ob Sie eine polynomielle Regression verwenden sollten, besteht darin, ein lineares Regressionsmodell an den Datensatz anzupassen und dann ein Diagramm der angepassten Werte gegen die Residuen für das Modell zu erstellen.

Wenn es einen klaren nichtlinearen Trend bei den Residuen gibt, deutet dies darauf hin, dass die polynomielle Regression möglicherweise eine bessere Anpassung an die Daten liefert.

Angenommen, wir passen ein lineares Regressionsmodell an, wobei wir die untersuchten Stunden als Prädiktorvariable und die Prüfungspunktzahl als Antwortvariable verwenden und dann das folgende Diagramm der angepassten Werte gegenüber den Residuen erstellen:

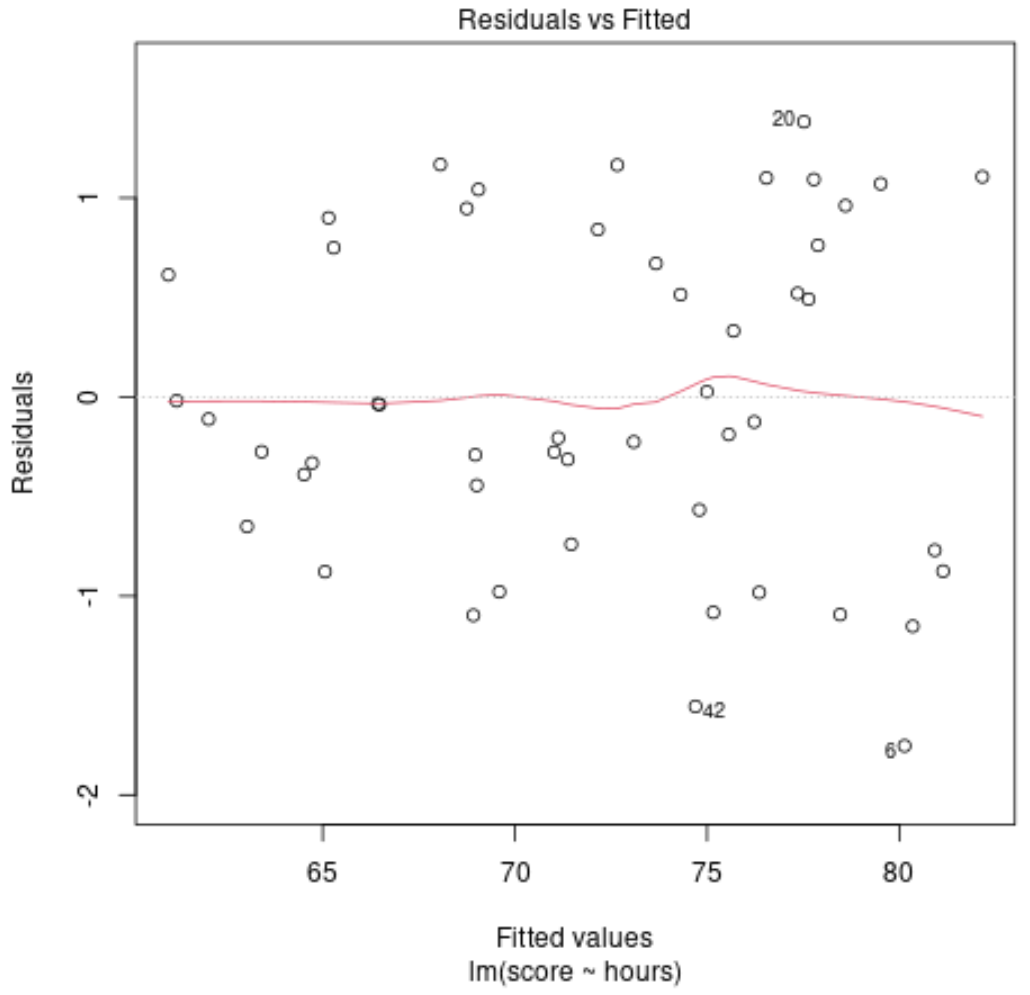
Die Residuen sind zufällig um Null herum verstreut und weisen kein klares Muster auf, was darauf hindeutet, dass ein lineares Modell eine angemessene Anpassung an die Daten liefert.

Nehmen wir jedoch an, dass unser Diagramm der angepassten Werte gegenüber den Residuen tatsächlich wie folgt aussieht:

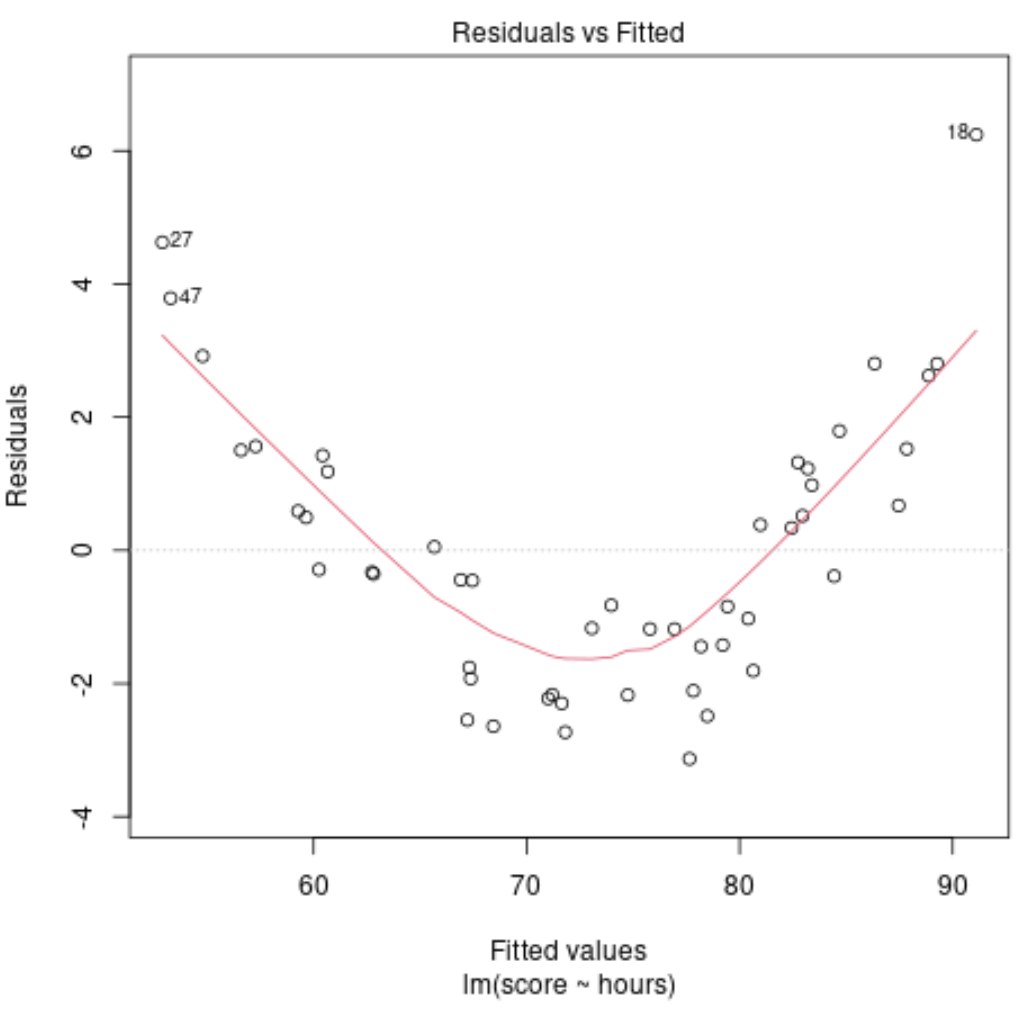
Aus der Grafik können wir erkennen, dass es ein klares nichtlineares Muster in den Residuen gibt – die Residuen weisen eine „U“-Form auf.

Dies zeigt uns, dass ein lineares Modell für diese speziellen Daten nicht geeignet ist und dass es sinnvoll sein könnte, stattdessen ein polynomiales Regressionsmodell anzupassen.

3. Berechnen Sie den angepassten R-Quadrat-Wert des Modells

Eine andere Möglichkeit zu bestimmen, ob Sie eine polynomielle Regression verwenden sollten, besteht darin, sowohl ein lineares Regressionsmodell als auch ein polynomiales Regressionsmodell anzupassen und die angepassten R-Quadrat-Werte für beide Modelle zu berechnen.

Das angepasste R-Quadrat stellt den Anteil der Varianz in der Antwortvariablen dar, der durch die Prädiktorvariablen im Modell erklärt werden kann, angepasst an die Anzahl der Prädiktorvariablen im Modell.

Das Modell mit dem höchsten angepassten R-Quadrat stellt das Modell dar, das die Prädiktorvariablen am besten zur Erklärung der Variation in der Antwortvariablen verwenden kann.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie eine Polynomregression mit unterschiedlicher Statistiksoftware durchführen:

Eine Einführung in die Polynomregression
So führen Sie eine Polynomregression in R durch
So führen Sie eine Polynomregression in Python durch
So führen Sie eine Polynomregression in Excel durch