Wann sollten sie einen boxplot verwenden? (3 szenarien)

Ein Boxplot ist eine Art Diagramm, das die fünfstellige Zusammenfassung eines Datensatzes anzeigt, der Folgendes umfasst:

• Der Mindestwert
• Das erste Quartil (das 25. Perzentil)
• Der Medianwert
• Das dritte Quartil (das 75. Perzentil)
• Der Maximalwert

Wir verwenden drei einfache Schritte, um ein Boxplot für einen beliebigen Datensatz zu erstellen:

• 1. Zeichnen Sie ein Kästchen vom ersten bis zum dritten Quartil
• 2. Zeichnen Sie eine vertikale Linie am Mittelwert
• 3. Zeichnen Sie „Whisker“ der Quartile zum Minimal- und Maximalwert

Normalerweise erstellen wir Boxplots in einem von drei Szenarios:

Szenario 1: Visualisieren Sie die Werteverteilung in einem Datensatz.

Mithilfe eines Boxplots können wir die Werteverteilung in einem Datensatz schnell visualisieren und sehen, wo sich die fünf numerischen Zusammenfassungswerte befinden.

Szenario 2: Vergleich von zwei oder mehr Verteilungen.

Mit Side-by-Side-Boxplots können wir die Unterschiede zwischen zwei oder mehr Verteilungen visualisieren und die Medianwerte und die Werteverteilung zwischen Verteilungen vergleichen.

Szenario 3: Ausreißer identifizieren.

In Boxplots werden Ausreißer normalerweise durch kleine Kreise dargestellt, die über jeden Whisker hinausragen. Eine Beobachtung wird als Ausreißer definiert, wenn sie eines der folgenden Kriterien erfüllt:

• Eine Beobachtung liegt unter Q1 – 1,5* (Interquartilbereich)
• Eine Beobachtung ist größer als Q3 + 1,5*(Interquartilbereich)

Durch die Erstellung eines Boxplots können wir schnell erkennen, ob eine Verteilung Ausreißer aufweist oder nicht.

Die folgenden Beispiele zeigen, wie wir in jedem Szenario einen Boxplot verwenden würden.

Szenario 1: Visualisieren Sie die Werteverteilung in einem Datensatz

Angenommen, ein Basketballtrainer möchte die Verteilung der von den Spielern seiner Mannschaft erzielten Punkte visualisieren und erstellt daher den folgenden Boxplot:

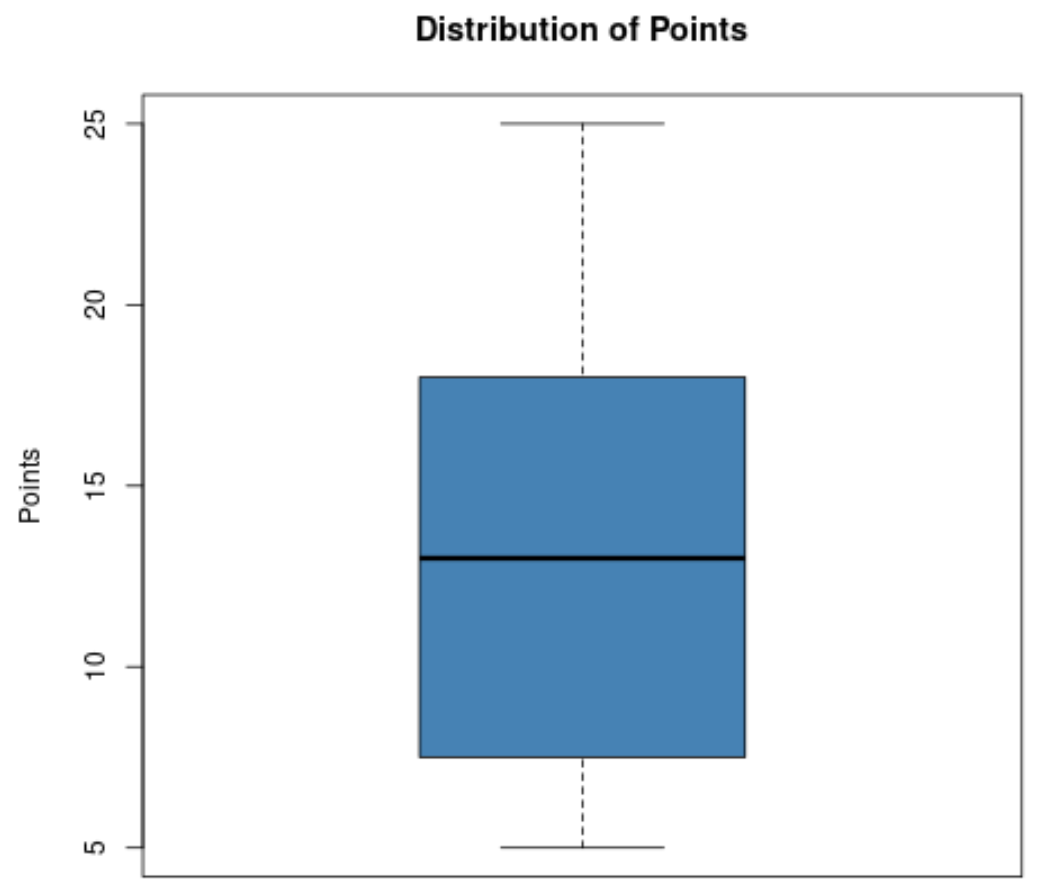
Anhand dieses Boxplots kann er schnell die folgenden Werte erkennen:

• Minimum: 5
• T1 (erstes Quartil): ungefähr 8
• Median: etwa 13
• T3 (drittes Quartil): ca. 18
• Maximal: 25

Dadurch kann der Trainer schnell erkennen, dass die von den Spielern erzielten Punkte zwischen 5 und 25 liegen, dass der erzielte Durchschnittspunkt bei etwa 13 liegt und dass 50 % seiner Spieler zwischen etwa 8 und 18 Punkten pro Spiel erzielen.

Szenario 2: Vergleichen Sie zwei oder mehr Verteilungen

Angenommen, ein Sportanalyst möchte die Verteilung der von Basketballspielern in drei verschiedenen Teams erzielten Punkte vergleichen und erstellt die folgenden Boxplots:

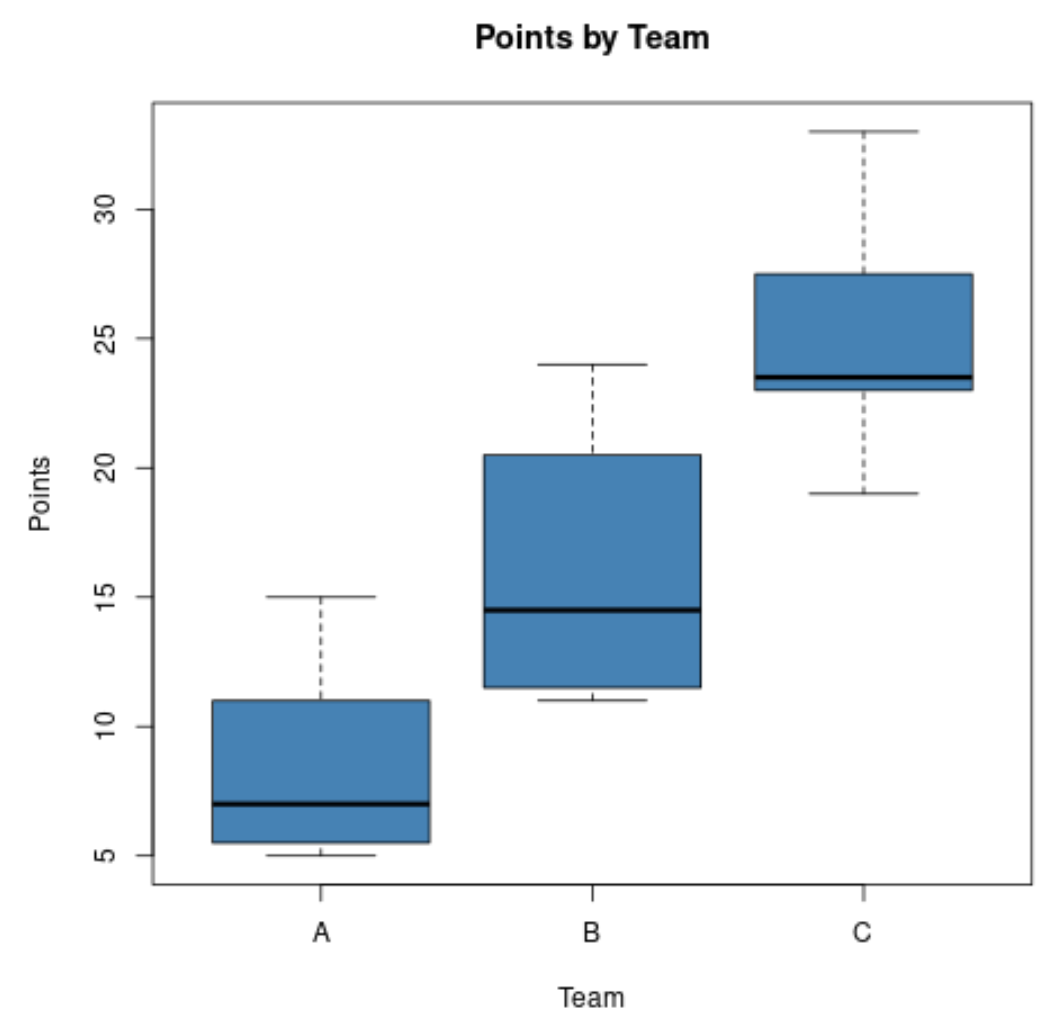
Anhand dieser Diagramme kann er schnell erkennen, dass Team C die meisten erzielten Mittelpunkte und Team A die niedrigsten erzielten Mittelpunkte hat.

Er kann auch schnell erkennen, dass Team B die größte Verteilung der erzielten Punkte hat, da Team Bs Boxplot die längste Box hat.

Szenario 3: Ausreißer identifizieren

Angenommen, ein Basketballtrainer möchte wissen, ob einer seiner Spieler hinsichtlich der erzielten Punkte ein Ausreißer ist. Er beschließt, das folgende Boxplot zu erstellen, um die Verteilung der von seinen Spielern erzielten Punkte zu visualisieren:

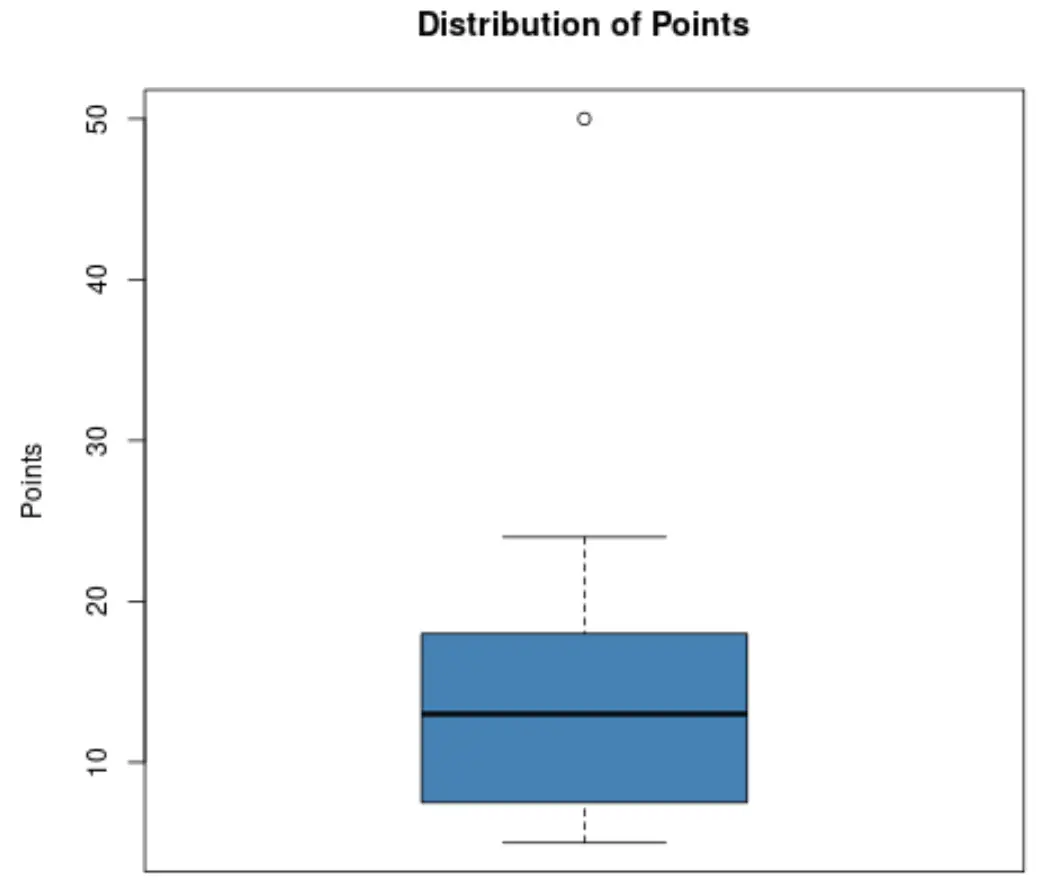
Anhand dieses Diagramms kann der Trainer erkennen, dass der kleine Punkt oben im Diagramm auf einen Ausreißer hinweist.

Konkret erzielte einer der Spieler rund 50 Punkte, was im Vergleich zu allen anderen erzielten Punkten als Ausreißer gilt.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten ausführliche Erklärungen zur praktischen Anwendung von Boxplots:

So ermitteln Sie den Interquartilbereich (IQR) eines Boxplots
So identifizieren Sie Asymmetrie in Boxplots
So vergleichen Sie Boxplots

Die folgenden Tutorials erklären, wie man Boxplots in verschiedenen Statistikprogrammen erstellt:

So erstellen Sie ein Boxplot in Google Sheets
So erstellen Sie Boxplots in SPSS
So erstellen Sie nebeneinander liegende Boxplots in Excel
So erstellen Sie Side-by-Side-Boxplots in R