Wann sollte die spearman-rangkorrelation verwendet werden (2 szenarien)

Die gebräuchlichste Methode zur Quantifizierung des linearen Zusammenhangs zwischen zwei Variablen ist die Verwendung des Pearson-Korrelationskoeffizienten , der immer einen Wert zwischen -1 und 1 annimmt, wobei:

• -1 zeigt eine vollkommen negative lineare Korrelation an
• 0 bedeutet keine lineare Korrelation
• 1 zeigt eine vollkommen positive lineare Korrelation an

Diese Art von Korrelationskoeffizient funktioniert jedoch am besten, wenn die tatsächliche zugrunde liegende Beziehung zwischen den beiden Variablen linear ist.

Es gibt einen anderen Typ von Korrelationskoeffizienten namens Spearman-Rangkorrelation , der am besten in zwei spezifischen Szenarien verwendet wird:

Szenario 1 : Bei der Arbeit mit klassifizierten Daten.

• Ein Beispiel könnte ein Datensatz sein, der die Rangfolge der Mathematikprüfungsergebnisse eines Schülers sowie die Rangfolge seiner naturwissenschaftlichen Prüfungsergebnisse in einer Klasse enthält.

Szenario 2 : Wenn ein oder mehrere extreme Ausreißer vorhanden sind.

• Wenn in einem Datensatz extreme Ausreißer vorhanden sind, wird der Pearson-Korrelationskoeffizient stark beeinflusst.

Die folgenden Beispiele zeigen, wie die Spearman-Rangkorrelation in jedem dieser Szenarios berechnet wird.

Szenario 1: Korrelation des Spearman-Rankings mit Ranglistendaten

Betrachten Sie den folgenden Datensatz (und das entsprechende Streudiagramm), der die Beziehung zwischen zwei Variablen zeigt:

Mithilfe einer Statistiksoftware können wir die folgenden Korrelationskoeffizienten für diese beiden Variablen berechnen:

• Pearson-Korrelation: 0,79
• Spearman-Rangkorrelation: 1

Wenn wir uns in diesem Szenario nur um den Rang der Datenwerte kümmern (wenn der Rang von x zunimmt, steigt dann auch der Rang von y?), dann würde uns die Rangkorrelation nach Spearman eine bessere Vorstellung davon geben Korrelation zwischen den beiden Variablen. .

In diesem speziellen Datensatz nimmt der Rang von y immer zu, wenn der Rang von x zunimmt.

Spearmans Rangkorrelation erfasst dieses Verhalten perfekt, indem sie uns sagt, dass zwischen den Rängen von x und den Rängen von y eine perfekte positive Beziehung ( ρ = 1 ) besteht.

Andererseits sagt uns die Pearson-Korrelation, dass zwischen den beiden Variablen eine starke lineare Beziehung ( r = 0,79 ) besteht.

Das ist wahr, aber es ist nicht sinnvoll, wenn wir uns nur um die Beziehung zwischen den Rängen von x und den Rängen von y kümmern.

Szenario 2: Korrelation des Spearman-Rankings mit extremen Ausreißern

Betrachten Sie den folgenden Datensatz (und das entsprechende Streudiagramm), der die Beziehung zwischen zwei Variablen zeigt:

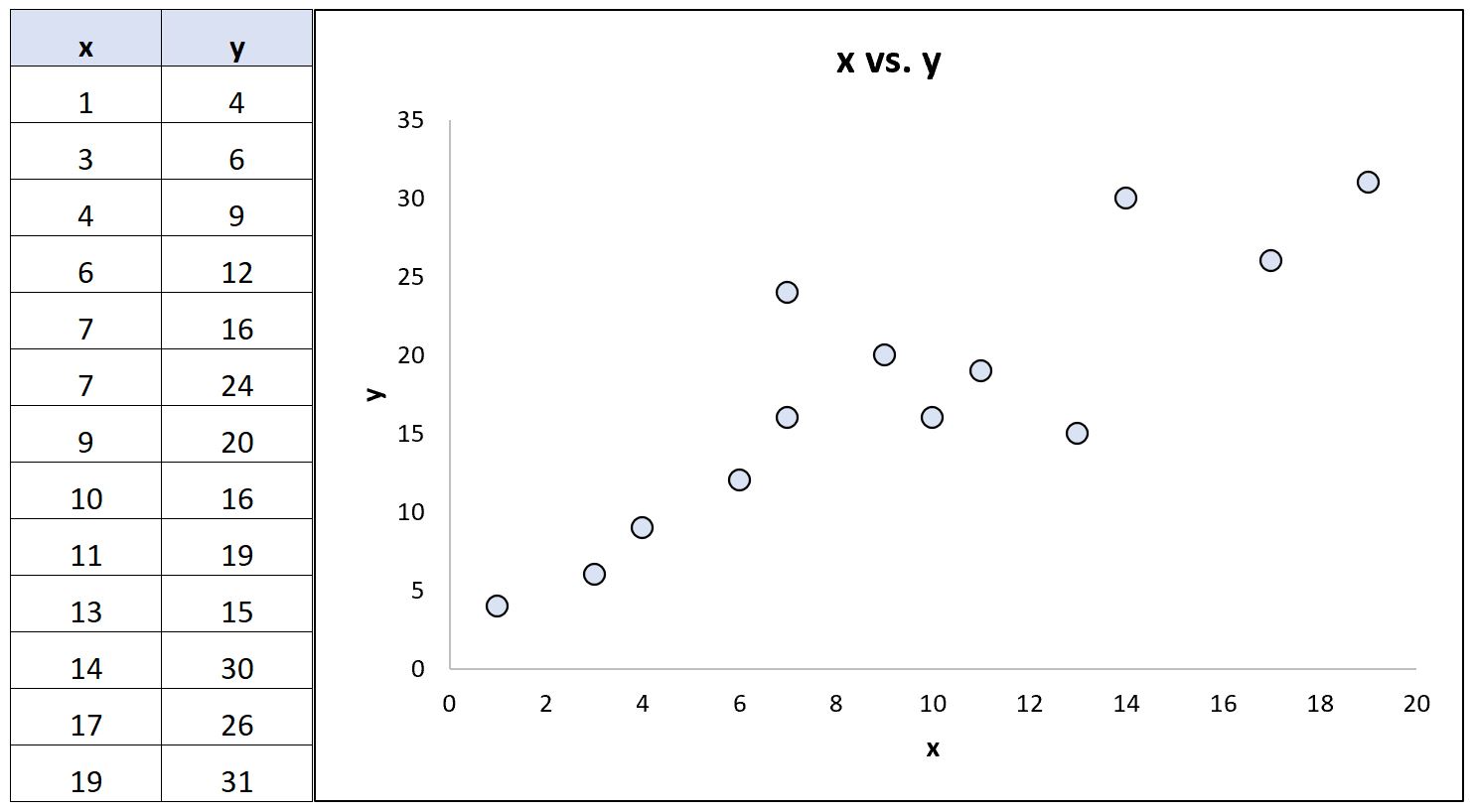
Mithilfe einer Statistiksoftware können wir die folgenden Korrelationskoeffizienten für diese beiden Variablen berechnen:

• Pearson-Korrelation: 0,86
• Spearman-Rangkorrelation: 0,85

Die Korrelationskoeffizienten sind nahezu identisch, da die zugrunde liegende Beziehung zwischen den Variablen annähernd linear ist und es keine extremen Ausreißer gibt.

Nehmen wir nun an, wir ändern den letzten y-Wert im Datensatz, sodass er zu einem extremen Ausreißer wird:

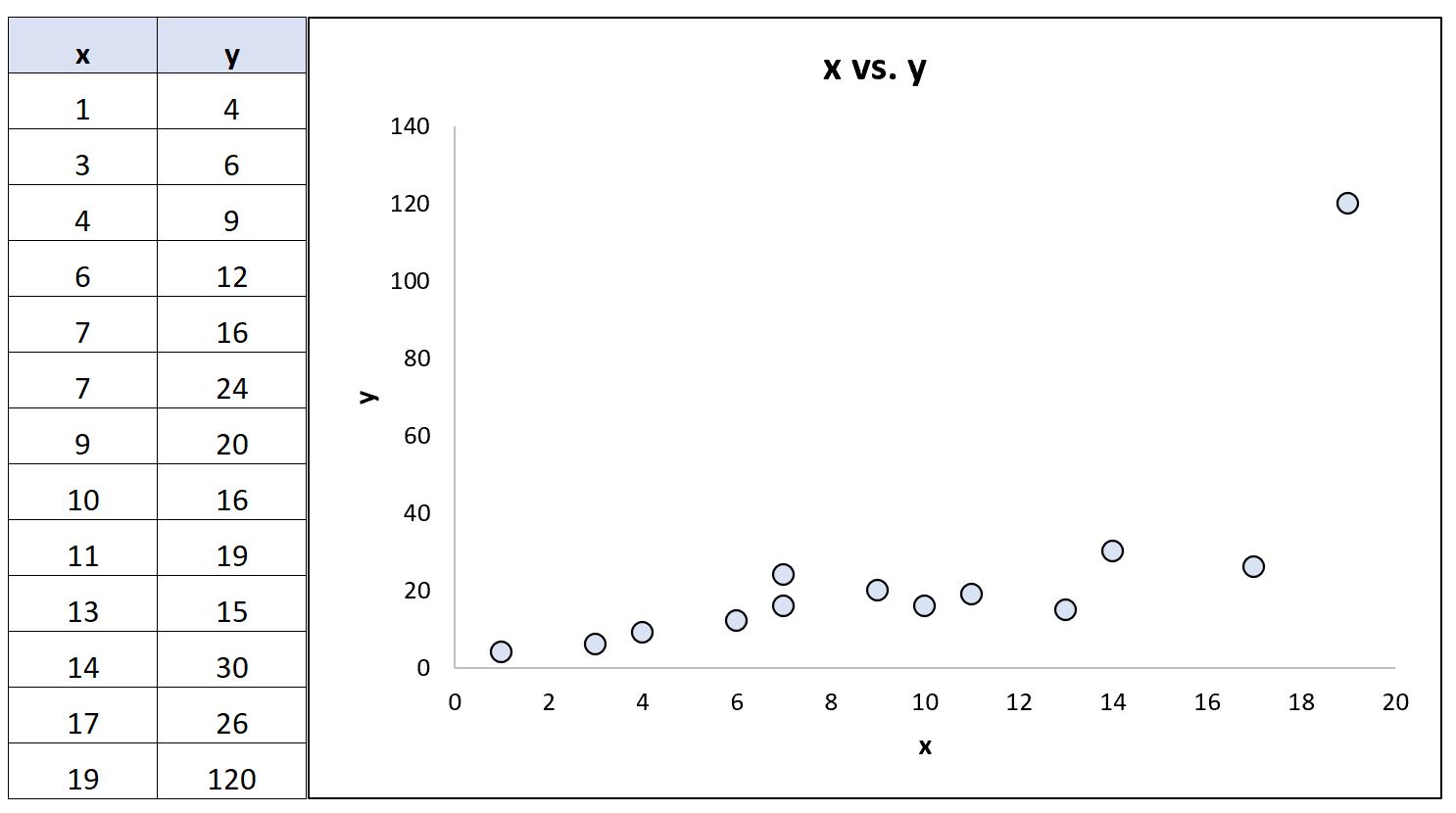
Mithilfe einer Statistiksoftware können wir die Korrelationskoeffizienten neu berechnen:

• Pearson-Korrelation: 0,69
• Spearman-Rangkorrelation: 0,85

Der Pearson-Korrelationskoeffizient änderte sich deutlich, während der Spearman-Rangkorrelationskoeffizient gleich blieb.

Im statistischen Fachjargon würden wir sagen, dass die Beziehung zwischen x und y monoton ist (wenn x zunimmt, nimmt y im Allgemeinen zu), aber nicht linear, da der Ausreißer die Daten stark beeinflusst.

In diesem Szenario quantifiziert die Rangkorrelation von Spearman diese monotone Beziehung gut, während die Korrelation von Pearson schlechte Ergebnisse liefert, da sie versucht, die lineare Beziehung zwischen den beiden Variablen zu berechnen.

Verwandte Themen: So melden Sie die Spearman-Rangkorrelation im APA-Format

Zusätzliche Ressourcen

Die folgenden Tutorials erklären, wie man die Spearman-Rangkorrelation mit unterschiedlicher Software berechnet:

So berechnen Sie die Spearman-Rangkorrelation in Excel
So berechnen Sie die Spearman-Rangkorrelation in Google Sheets
So berechnen Sie die Spearman-Rangkorrelation in R
So berechnen Sie die Spearman-Rangkorrelation in Python