Warum ist die standardabweichung wichtig? (erklärung + beispiele)

Die Standardabweichung wird verwendet, um die Werteverteilung in einer Stichprobe zu messen.

Mit der folgenden Formel können wir die Standardabweichung einer bestimmten Stichprobe berechnen:

√ Σ(x _i – x _bar ) ² / (n-1)

Gold:

• Σ: Ein Symbol, das „Summe“ bedeutet
• x _i : der ^i-te Wert der Stichprobe
• x _bar : Der Stichprobenmittelwert
• n: Die Stichprobengröße

Je höher der Standardabweichungswert ist, desto stärker sind die Werte in einer Stichprobe gestreut. Umgekehrt gilt: Je niedriger der Standardabweichungswert, desto enger sind die Werte geclustert.

Eine von Studierenden häufig gestellte Frage lautet: Warum ist die Standardabweichung wichtig?

Die Antwort: Die Standardabweichung ist wichtig, weil sie uns die Verteilung der Werte in einem bestimmten Datensatz verrät.

Wir analysieren einen Datensatz. Wann immer wir die folgenden Metriken finden möchten:

• Das Zentrum des Datensatzes . Die gebräuchlichste Methode zur Messung der „Mitte“ ist die Verwendung des Mittelwerts und des Medians.
• Die Verteilung der Werte im Datensatz . Die gebräuchlichste Methode zur Messung der Streuung ist die Verwendung der Standardabweichung.

Indem wir wissen, wo sich das Zentrum befindet und wie die Werteverteilung ist, können wir die Werteverteilung in jedem Datensatz gut verstehen.

Die folgenden Beispiele verdeutlichen die Bedeutung der Standardabweichung in der Praxis.

Beispiel 1: Gehaltsverteilung

Angenommen, das Durchschnittsgehalt bei Unternehmen A beträgt 80.000 US-Dollar und die Standardabweichung beträgt 20.000 US-Dollar. Da die Standardabweichung so groß ist, gibt es keine Garantie dafür, dass Sie annähernd 80.000 US-Dollar pro Jahr verdienen, wenn Sie in diesem Unternehmen arbeiten, da es große Gehaltsunterschiede gibt.

Nehmen wir umgekehrt an, dass das Durchschnittsgehalt bei Unternehmen B ebenfalls 80.000 US-Dollar beträgt, die Standardabweichung jedoch nur 4.000 US-Dollar beträgt. Da diese Standardabweichung so gering ist, können Sie sicher sein, dass Sie nahezu 80.000 US-Dollar erhalten, da es bei den Gehältern nur sehr geringe Schwankungen gibt.

Wenn wir ein Boxplot erstellen würden, um die Gehaltsverteilung bei diesen beiden Unternehmen zu visualisieren, könnte das so aussehen:

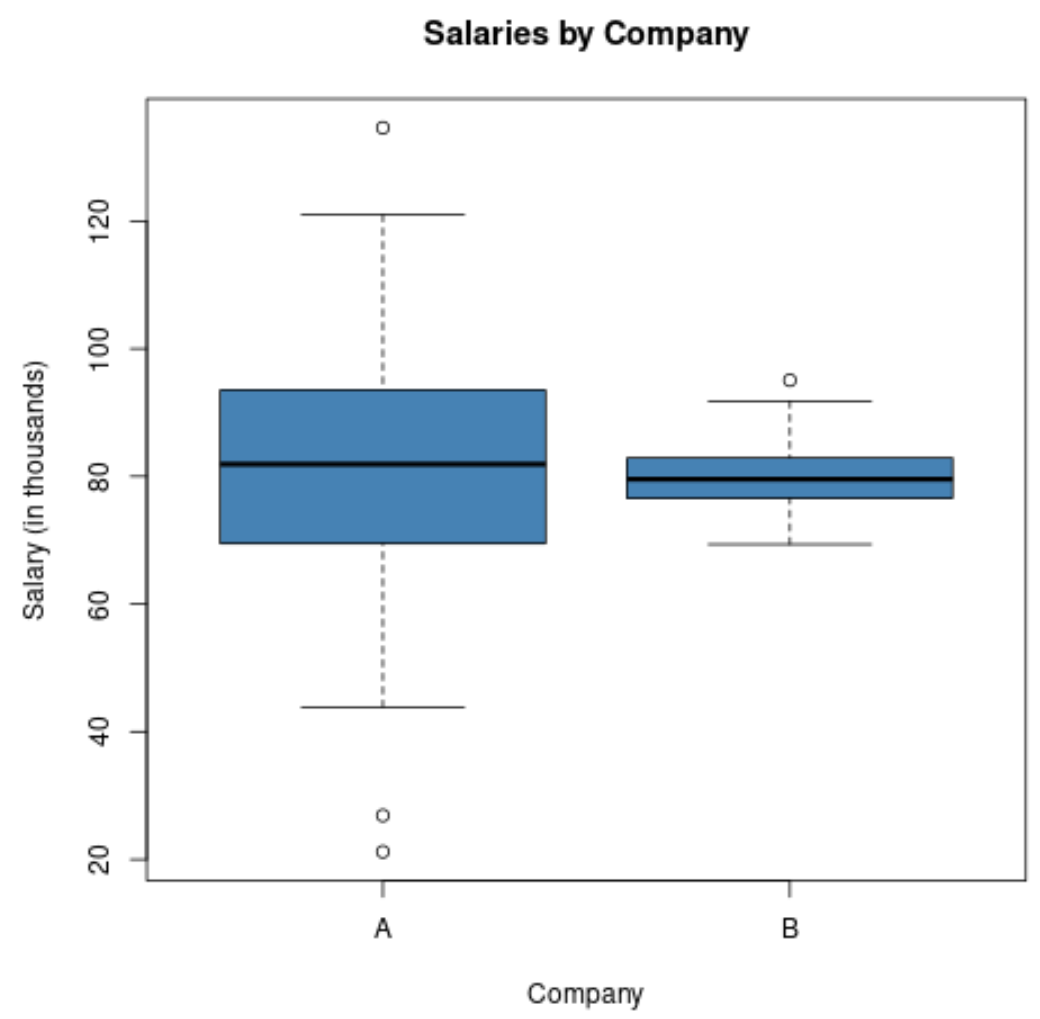
Beachten Sie, dass die Länge des Boxplots für Unternehmen A größer ist, da die Standardabweichung der Löhne viel höher ist.

Beide Unternehmen haben das gleiche Durchschnittsgehalt, in Unternehmen A ist der Gehaltsunterschied jedoch deutlich höher.

Beispiel 2: Verteilung der Immobilienpreise

Angenommen, der durchschnittliche Immobilienpreis in Nachbarschaft A beträgt 250.000 US-Dollar und die Standardabweichung beträgt 50.000 US-Dollar. Da die Standardabweichung ziemlich groß ist, bedeutet dies, dass einige Hauspreise viel höher als 250.000 US-Dollar und andere viel niedriger sein werden. Wenn Sie sich ein bestimmtes Haus in dieser Gegend ansehen, gibt es keine Garantie dafür, dass der Preis auch nur annähernd dem Durchschnitt entspricht.

Nehmen wir umgekehrt an, dass der durchschnittliche Hauspreis in Nachbarschaft B ebenfalls 250.000 US-Dollar beträgt, die Standardabweichung jedoch nur 10.000 US-Dollar beträgt. Da diese Standardabweichung recht gering ist, können Sie sicher sein, dass jedes Haus, das Sie sich in der Nachbarschaft ansehen, wahrscheinlich für diesen Preis geeignet ist.

Wenn wir ein Boxplot erstellen würden, um die Verteilung der Immobilienpreise in diesen beiden Stadtteilen zu visualisieren, könnte es so aussehen:

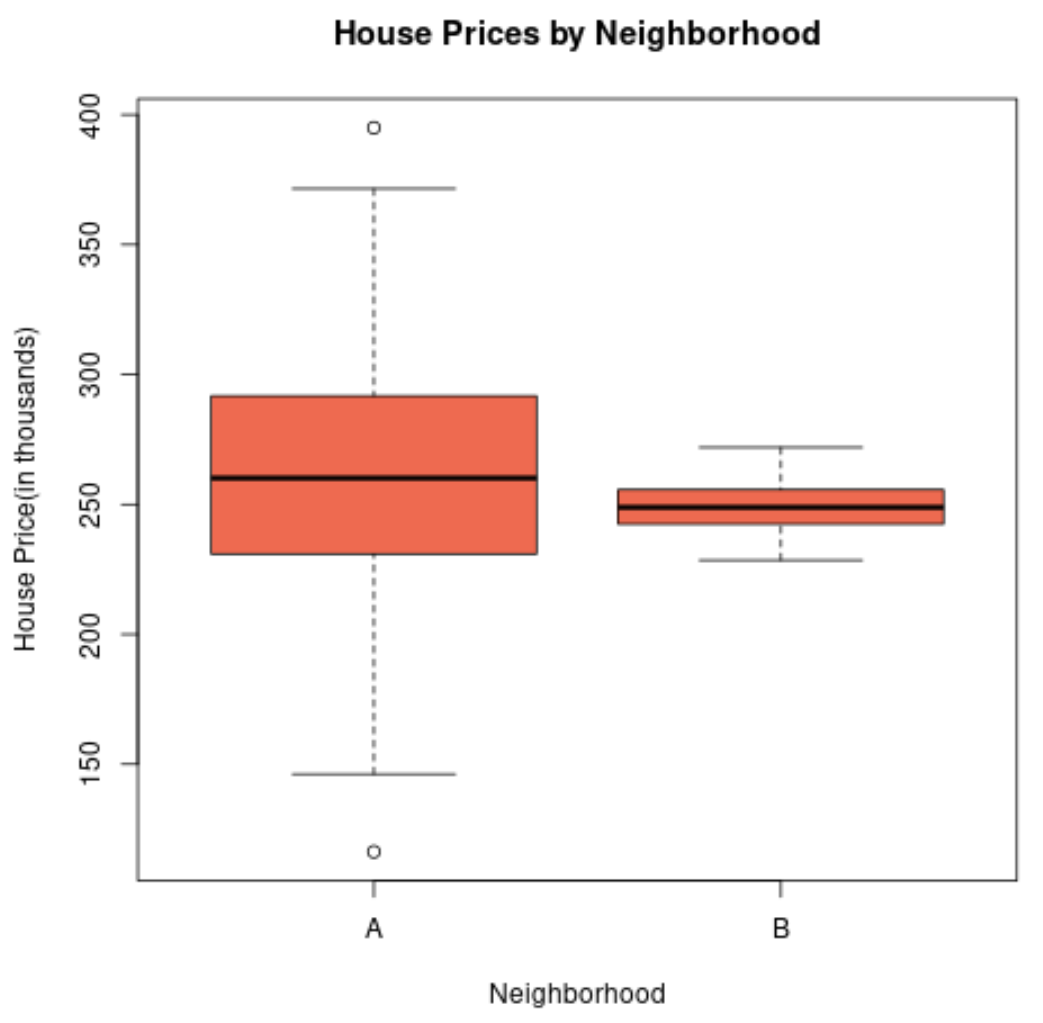
Die Länge des Boxplots von Stadtteil A ist größer, da die Standardabweichung der Immobilienpreise viel höher ist.

Tatsächlich liegen die Immobilienpreise für Stadtteil A zwischen weniger als 150.000 und über 400.000 US-Dollar, während die Preise für Stadtteil B nur zwischen etwa 230.000 und 270.000 US-Dollar liegen.

Indem wir einfach die Standardabweichung der Immobilienpreise in den einzelnen Stadtteilen kennen, können wir wissen, wie stark die Preisschwankungen in den einzelnen Stadtteilen zu erwarten sind.

Zusätzliche Ressourcen

Was gilt als gute Standardabweichung?
Reichweite vs. Standardabweichung: Wann jeweils zu verwenden ist
Variationskoeffizient versus Standardabweichung: die Differenz