Was bedeutet es, wenn eine statistik belastbar ist?

Eine Statistik wird als resilient bezeichnet, wenn sie nicht auf Extremwerte reagiert.

Hier sind zwei Beispiele für belastbare Statistiken:

• Der Median
• Der Interquartilbereich

Hier sind Beispiele für Statistiken, die nicht standhalten :

• Der Durchschnitt
• Die Standardabweichung
• Ordentlich

Das folgende Beispiel veranschaulicht den Unterschied zwischen resilienten und nicht-resistenten Statistiken.

Beispiel: Resistente und nicht-resistente Statistiken

Angenommen, wir haben den folgenden Datensatz:

Datensatz: 2, 5, 6, 7, 8, 13, 15, 18, 22, 24, 29

Mithilfe eines Taschenrechners oder einer Statistiksoftware können wir den Wert der folgenden Bestandsstatistiken für diesen Datensatz berechnen:

• Median: 13
• Interquartilbereich: 13,5

Wir können auch den Wert der folgenden nicht belastbaren Statistiken für diesen Datensatz berechnen:

• Durchschnitt: 13,54
• Standardabweichung: 8,82
• Bereich: 27

Überlegen Sie nun, ob diesem Datensatz ein extremer Ausreißer hinzugefügt wurde:

Datensatz: 2, 5, 6, 7, 8, 13, 15, 18, 22, 24, 29, 450

Wir können den Wert der folgenden belastbaren Statistiken für diesen Datensatz erneut berechnen:

• Median: 14
• Interquartilbereich: 15,75

Wir können auch den Wert der folgenden nicht belastbaren Statistiken für diesen Datensatz berechnen:

• Durchschnitt: 49,92
• Standardabweichung: 126,27
• Bereich: 448

Beachten Sie, wie sehr sich die Nicht-Widerstandsstatistik geändert hat, indem Sie einfach einen Extremwert zum Datensatz hinzugefügt haben:

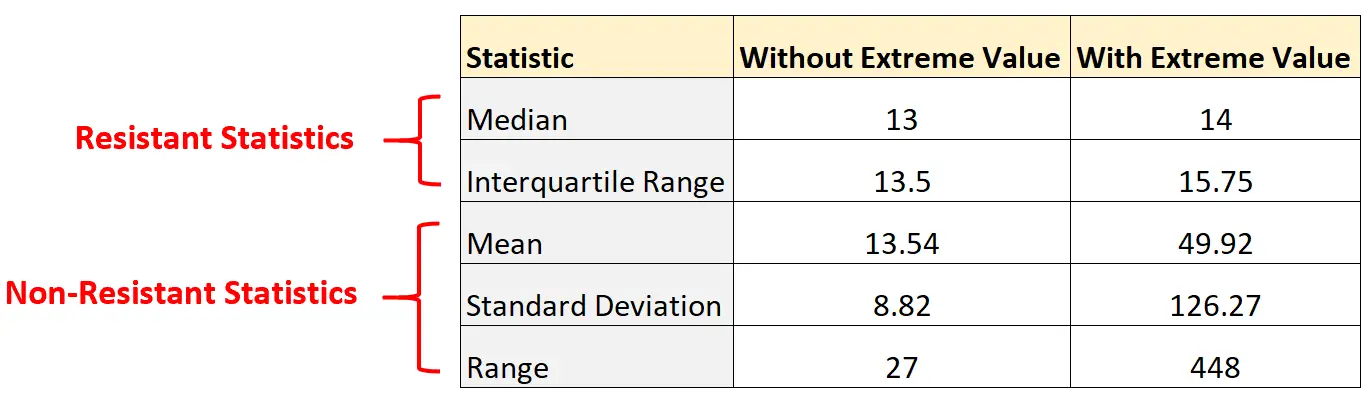
Die Statistiken der Widerstandskämpfer haben sich hingegen kaum verändert. Der Median und der Interquartilbereich veränderten sich nur geringfügig.

Wann sollten belastbare Statistiken verwendet werden?

Die am häufigsten verwendeten Statistiken zur Messung des Mittelpunkts und der Streuung von Werten in einem Datensatz sind der Mittelwert bzw. die Standardabweichung.

Leider reagieren beide Statistiken empfindlich auf Extremwerte. Wenn also Ausreißer in einem Datensatz vorhanden sind, beschreiben Mittelwert und Standardabweichung die Verteilung der Werte in einem Datensatz nicht genau.

Stattdessen wird empfohlen, den Median und den Interquartilbereich zu verwenden, um die Mitte und Streuung von Werten in einem Datensatz zu messen, wenn Ausreißer vorhanden sind, da beide Statistiken robust sind.

Zusätzliche Ressourcen

Wie wirken sich Ausreißer auf den Mittelwert aus?
Wann sollte der Mittelwert gegenüber dem Median verwendet werden?
Wann sollte der Interquartilbereich im Vergleich zur Standardabweichung verwendet werden?