Was gilt als „schwach“; korrelation?
In der Statistik versuchen wir oft zu verstehen, wie zwei Variablen zueinander in Beziehung stehen. Zum Beispiel möchten wir vielleicht wissen:
- Welcher Zusammenhang besteht zwischen der Anzahl der Stunden, die ein Student lernt, und der Note, die er bei der Prüfung erhält?
- Welcher Zusammenhang besteht zwischen der Außentemperatur und der Anzahl der von einem Imbisswagen verkauften Eisriegel?
- Welches Verhältnis besteht zwischen den für Werbung ausgegebenen Dollars und dem Gesamtumsatz eines bestimmten Unternehmens?
In jedem Szenario möchten wir die Beziehung zwischen zwei Variablen verstehen.
Eine der gebräuchlichsten Methoden zur Quantifizierung einer Beziehung zwischen zwei Variablen ist die Verwendung des Pearson-Korrelationskoeffizienten , der ein Maß für den linearen Zusammenhang zwischen zwei Variablen ist.
Es nimmt immer einen Wert zwischen -1 und 1 an, wobei:
- -1 zeigt eine vollkommen negative lineare Korrelation zwischen zwei Variablen an
- 0 bedeutet, dass zwischen zwei Variablen keine lineare Korrelation besteht
- 1 zeigt eine vollkommen positive lineare Korrelation zwischen zwei Variablen an
Diese oft mit r bezeichnete Zahl hilft uns, die Stärke der Beziehung zwischen zwei Variablen zu verstehen. Je näher r an Null liegt, desto schwächer ist der Zusammenhang zwischen den beiden Variablen .
Es ist wichtig zu beachten, dass zwei Variablen eine schwache positive Korrelation oder eine schwache negative Korrelation aufweisen können.
Schwache positive Korrelation: Wenn eine Variable zunimmt, nimmt die andere Variable tendenziell ebenfalls zu, jedoch nur schwach oder unzuverlässig.
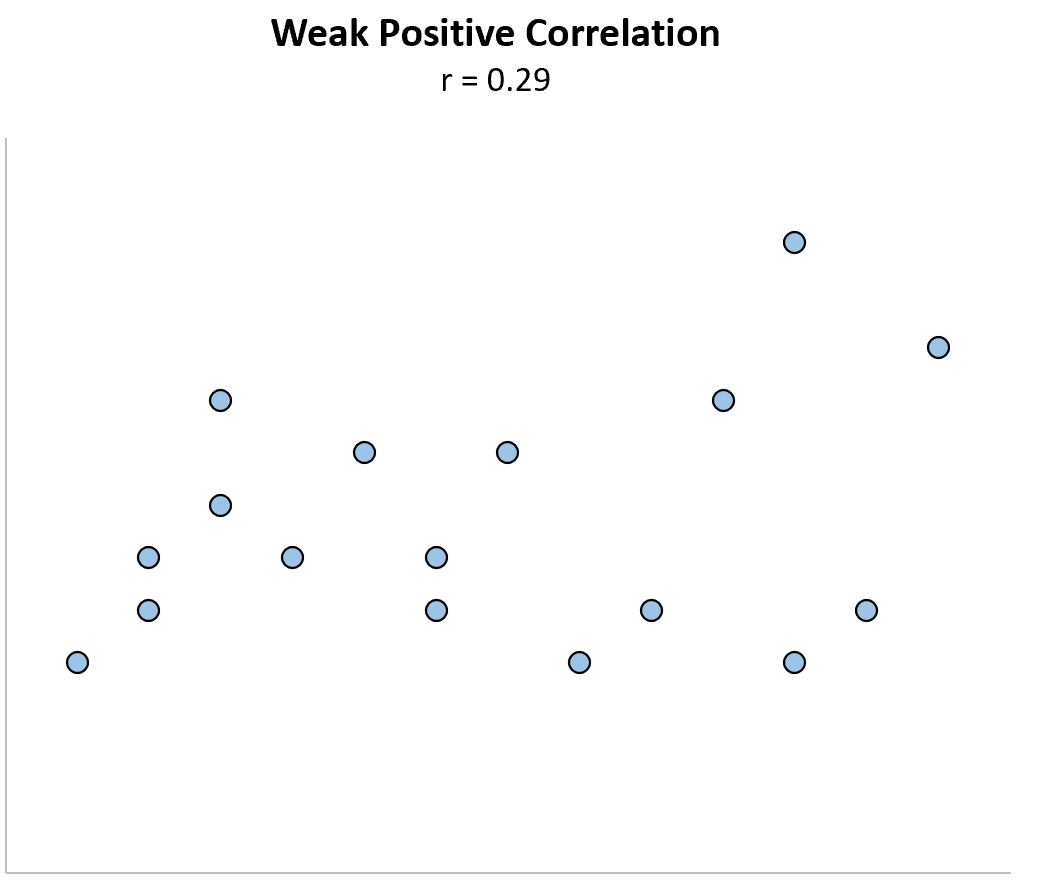
Geringe negative Korrelation: Wenn eine Variable zunimmt, nimmt die andere Variable tendenziell ab, jedoch nur schwach oder unzuverlässig.
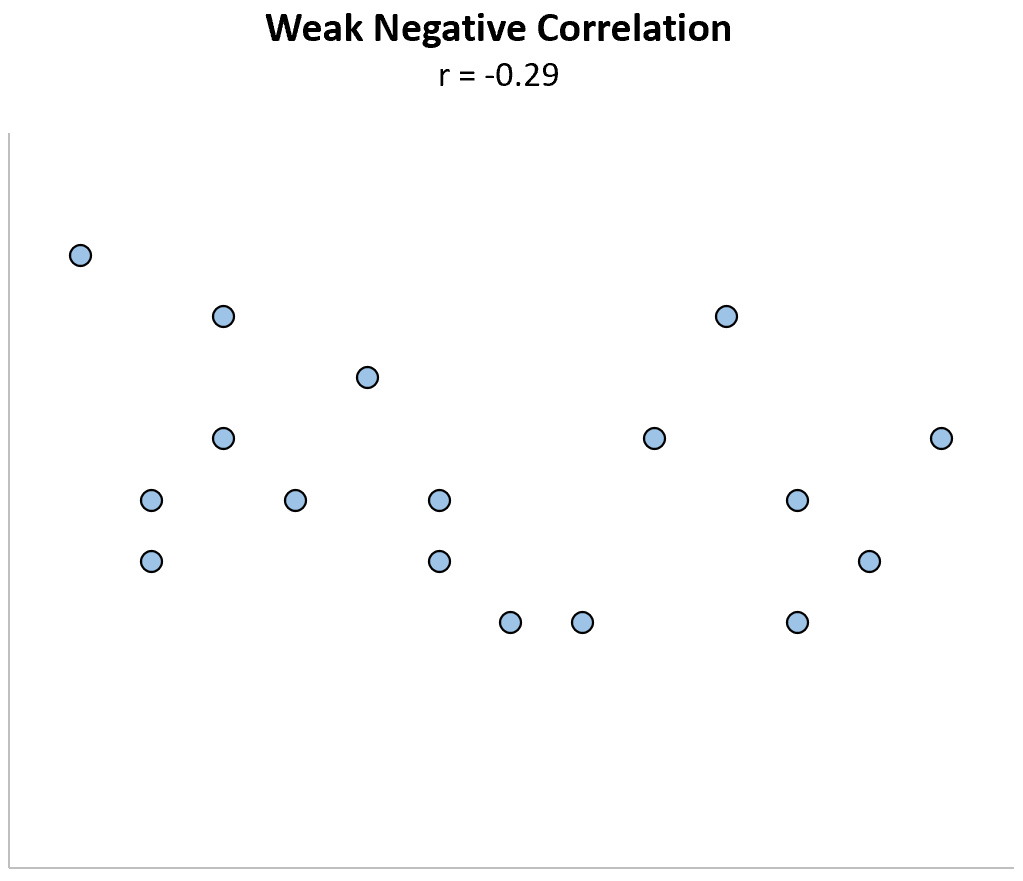
Die folgende Tabelle zeigt die Faustregel zur Interpretation der Stärke der Beziehung zwischen zwei Variablen basierend auf dem Wert von r :
| Absoluter Wert von r | Stärke der Beziehung |
|---|---|
| r < 0,25 | Keine Beziehung |
| 0,25 < r < 0,5 | Schwache Beziehung |
| 0,5 < r < 0,75 | Moderate Beziehungen |
| r > 0,75 | Starke Beziehung |
Die Korrelation zwischen zwei Variablen gilt als gering, wenn der Absolutwert von r zwischen 0,25 und 0,5 liegt.
Allerdings kann die Definition einer „schwachen“ Korrelation von Fachgebiet zu Fachgebiet unterschiedlich sein.
Medizinisch
Im medizinischen Bereich ist die Definition einer „schwachen“ Beziehung oft viel niedriger. Wenn der Zusammenhang zwischen der Einnahme eines bestimmten Arzneimittels und der Verringerung von Herzinfarkten r = 0,2 beträgt, könnte dies in anderen Bereichen als „kein Zusammenhang“ angesehen werden, in der Medizin ist er jedoch signifikant genug, dass es sich lohnt, das Arzneimittel einzunehmen, um das Risiko von Herzinfarkten zu verringern . einen Herzinfarkt haben.
Personalwesen
In einem Bereich wie dem Personalwesen werden auch häufiger niedrigere Korrelationen verwendet. Beispielsweise hat sich gezeigt, dass die Korrelation zwischen dem Hochschuldurchschnitt und der Arbeitsleistung etwa r = 0,16 beträgt. Das ist ziemlich niedrig, aber wichtig genug, dass ein Unternehmen dies zumindest während eines Vorstellungsgesprächs berücksichtigen sollte.
Technologie
In Technologiebereichen muss die Korrelation zwischen Variablen möglicherweise viel höher sein, um als „niedrig“ zu gelten. Wenn ein Unternehmen beispielsweise ein selbstfahrendes Auto entwickelt und die Korrelation zwischen den Abbiegeentscheidungen des Autos und der Wahrscheinlichkeit, einen Unfall zu vermeiden, r = 0,95 beträgt, kann dies als „schwache“ Korrelation angesehen werden und ist wahrscheinlich zu schwach für das Auto als sicher gelten, denn eine falsche Entscheidung kann tödlich sein.
Verwenden Sie Streudiagramme, um Zusammenhänge zu visualisieren
Bei der Berechnung des Korrelationskoeffizienten zwischen zwei Variablen ist es sinnvoll, ein Streudiagramm zu erstellen, um auch die Korrelation zu visualisieren.
Punktwolken bieten insbesondere zwei Vorteile:
1. Streudiagramme können Ihnen dabei helfen, Ausreißer zu identifizieren, die sich auf den Korrelationskoeffizienten auswirken.
Ein extremer Ausreißer kann einen großen Einfluss auf den Korrelationskoeffizienten haben. Betrachten Sie das folgende Beispiel, in dem die Variablen X und Y einen Pearson-Korrelationskoeffizienten von r = 0,91 haben.
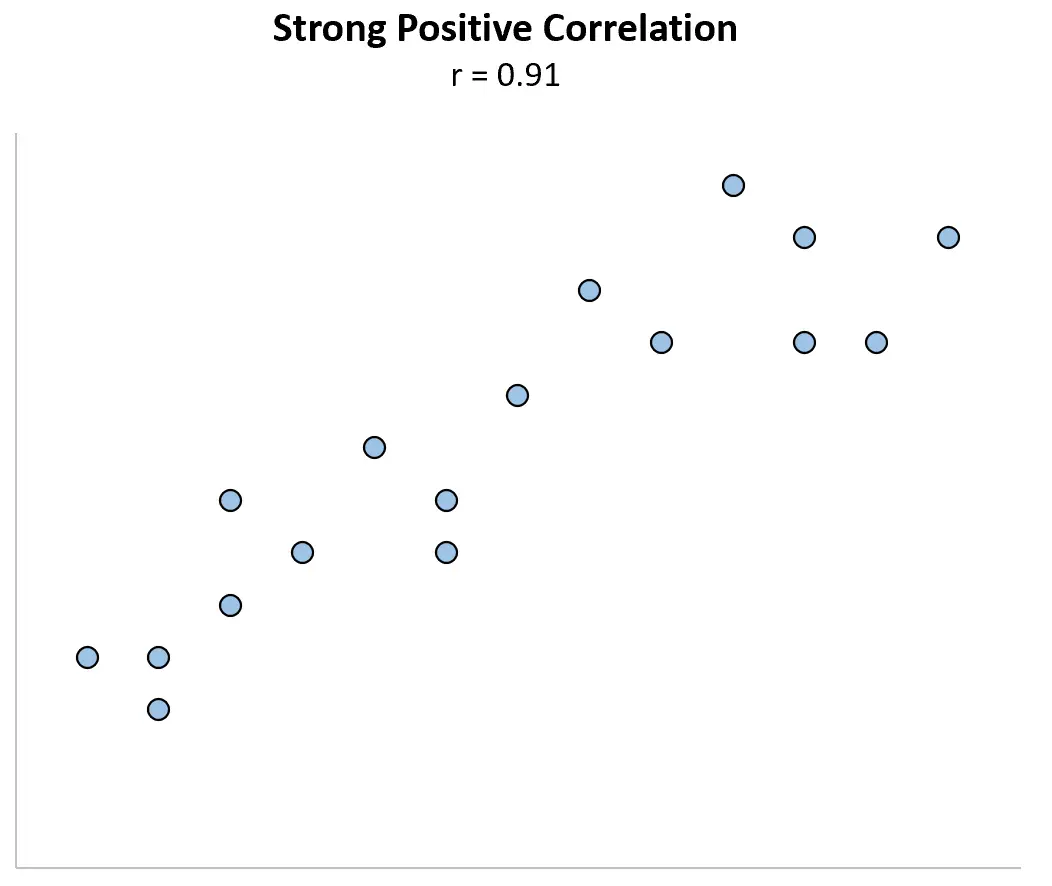
Stellen Sie sich nun vor, wir ändern den ersten Datenpunkt so, dass er viel größer wird. Der Korrelationskoeffizient beträgt plötzlich r = 0,29 .
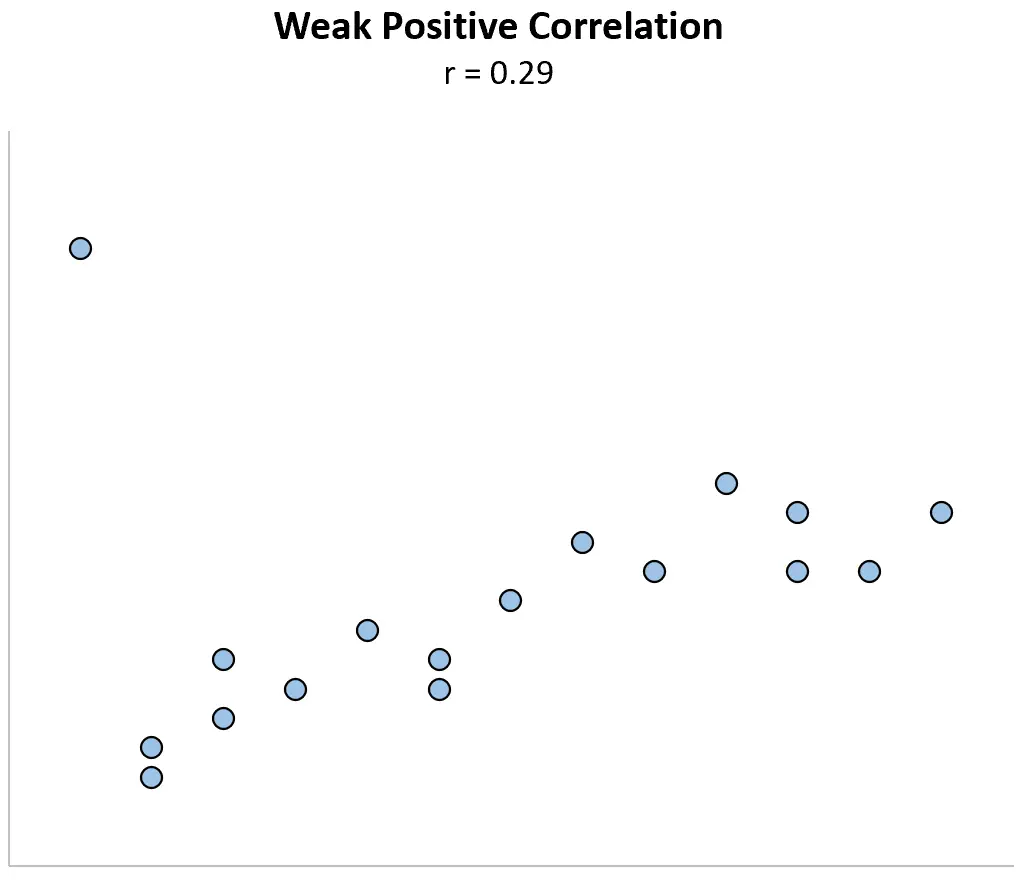
Dieser einzelne Datenpunkt ändert den Korrelationskoeffizienten von einer stark positiven Beziehung zu einer schwach positiven Beziehung.
(2) Streudiagramme können Ihnen helfen, nichtlineare Beziehungen zwischen Variablen zu identifizieren.
Ein Pearson-Korrelationskoeffizient sagt uns einfach, ob zwei Variablen linear miteinander verbunden sind. Aber selbst wenn uns ein Pearson-Korrelationskoeffizient sagt, dass zwei Variablen nicht korreliert sind, könnte zwischen ihnen dennoch eine Art nichtlineare Beziehung bestehen.
Betrachten Sie beispielsweise das Streudiagramm unten zwischen den Variablen X und Y , in dem ihre Korrelation r = 0,00 beträgt.
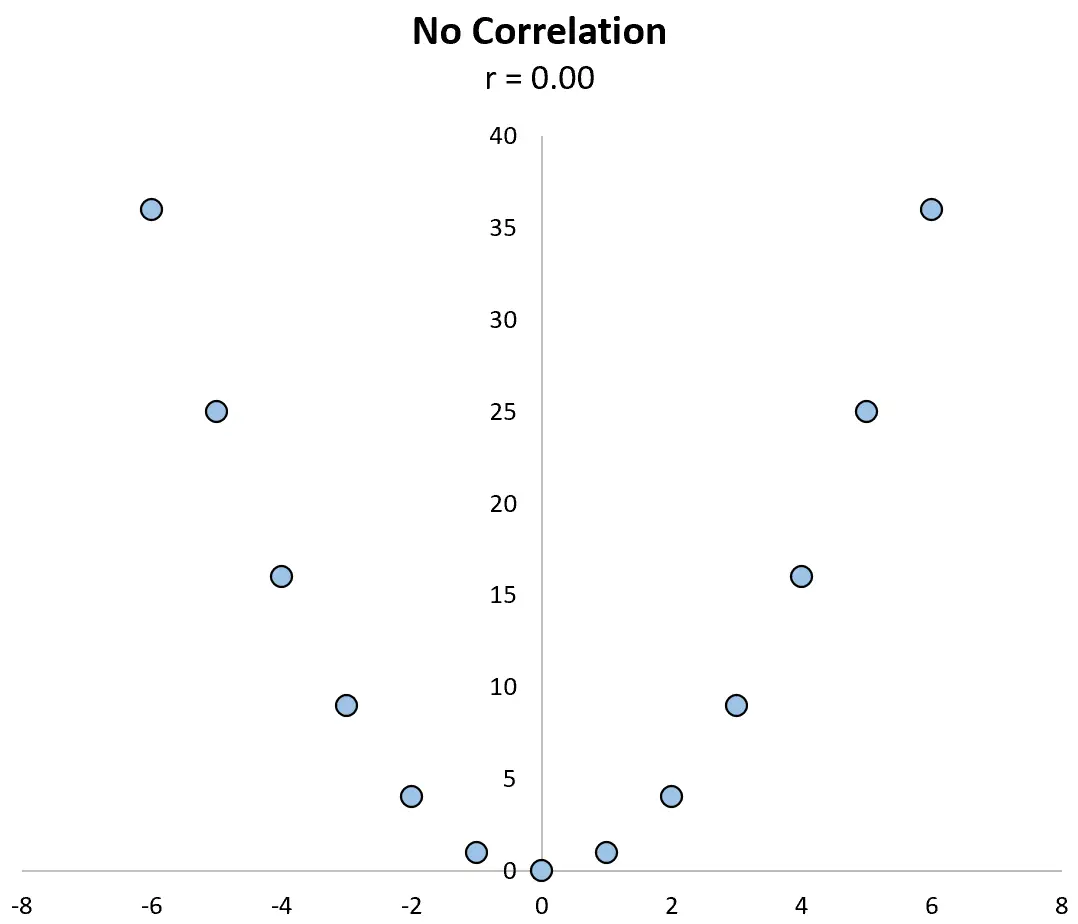
Die Variablen haben eindeutig keine lineare Beziehung, aber sie haben eine nichtlineare Beziehung: Die y-Werte sind einfach die x-Werte im Quadrat.
Ein Korrelationskoeffizient allein konnte diesen Zusammenhang nicht erkennen, ein Streudiagramm jedoch schon.
Abschluss
In Summe:
1. Im Allgemeinen gilt ein Korrelationskoeffizient zwischen 0,25 und 0,5 als „schwache“ Korrelation zwischen zwei Variablen.
2. Diese Faustregel kann von Gebiet zu Gebiet unterschiedlich sein. Beispielsweise könnte eine viel geringere Korrelation in einem medizinischen Bereich im Vergleich zu einem technologischen Bereich als schwach angesehen werden. Stellen Sie sicher, dass Sie Ihr Fachwissen nutzen, um zu entscheiden, was als geringe Korrelation gilt.
3. Wenn Sie einen Korrelationskoeffizienten verwenden, um die Beziehung zwischen zwei Variablen zu beschreiben, ist es auch hilfreich, ein Streudiagramm zu erstellen, damit Sie Ausreißer im Datensatz sowie eine mögliche nichtlineare Beziehung identifizieren können.
Zusätzliche Ressourcen
Was gilt als „starke“ Korrelation?
Korrelationsmatrix-Rechner
Korrelation vs. Assoziation: Was ist der Unterschied?