Weibull-verteilung
In diesem Artikel wird erklärt, was die Weibull-Verteilung ist und wofür sie verwendet wird. Darüber hinaus können Sie die grafische Darstellung der Weibull-Verteilung und die Eigenschaften dieser Art von Wahrscheinlichkeitsverteilung sehen.
Was ist die Weibull-Verteilung?
Die Weibull-Verteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung, die durch zwei charakteristische Parameter definiert ist: den Formparameter α und den Skalenparameter λ.
In der Statistik wird die Weibull-Verteilung hauptsächlich zur Überlebensanalyse verwendet. Ebenso hat die Weibull-Verteilung viele Anwendungen in verschiedenen Bereichen. Im Folgenden gehen wir detailliert auf die Verwendung der Weibull-Verteilung ein.
![]()
Den Autoren zufolge lässt sich die Weibull-Verteilung auch mit drei Parametern parametrisieren. Dann wird ein dritter Parameter namens Schwellenwert hinzugefügt, der die Abszisse angibt, bei der das Verteilungsdiagramm beginnt.
Die Weibull-Verteilung ist nach dem Schweden Waloddi Weibull benannt, der sie 1951 ausführlich beschrieb. Allerdings wurde die Weibull-Verteilung 1927 von Maurice Fréchet entdeckt und erstmals 1933 von Rosin und Rammler angewendet.
Darstellung der Weibull-Verteilung
Sobald wir die Definition der Weibull-Verteilung kennengelernt haben, werden wir sehen, wie sich ihre grafische Darstellung abhängig von den Werten ihrer Parameter ändert.
Unten sehen Sie mehrere Beispiele dafür, wie sich der Dichtefunktionsgraph der Weibull-Verteilung abhängig vom Wert des Formparameters und des Skalenparameters ändert.
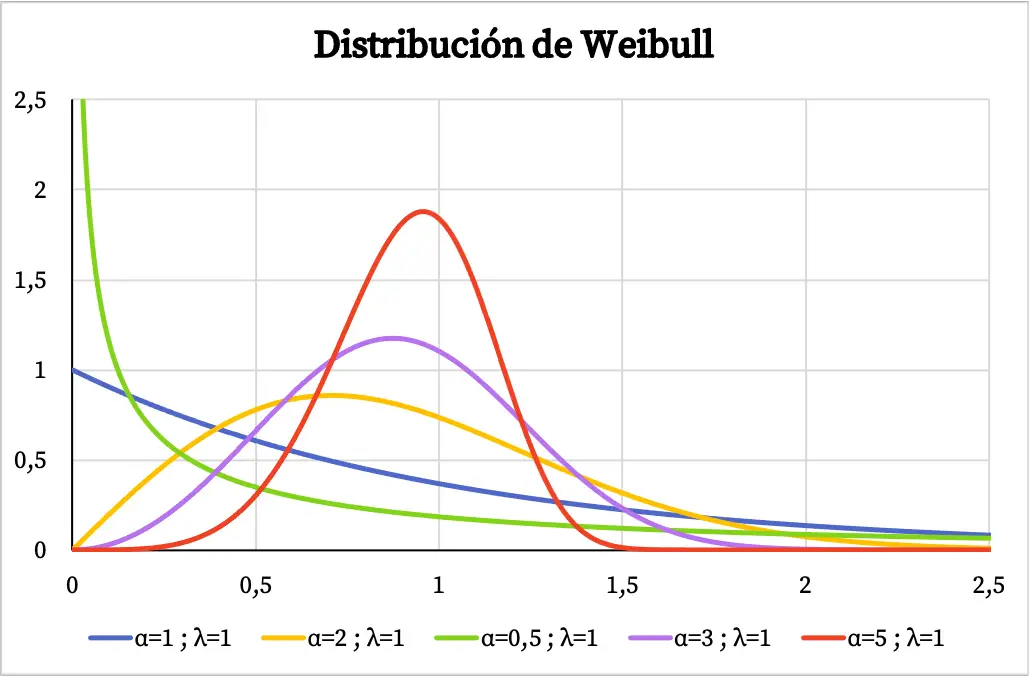
Wenn die Weibull-Verteilung zur Modellierung der Ausfallrate eines Systems als Funktion der Zeit verwendet wird, bedeutet der Wert des Formparameters α Folgendes:
- α<1: Die Ausfallrate nimmt mit der Zeit ab.
- α=1: Die Ausfallrate ist über die Zeit konstant.
- α>1: Die Ausfallrate steigt mit der Zeit.
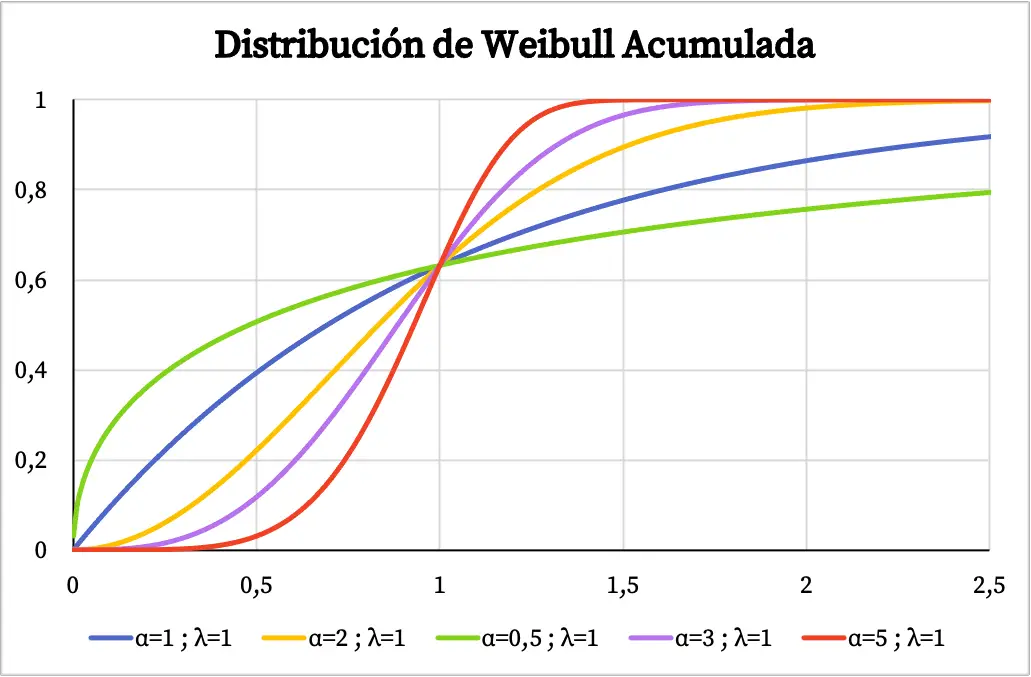
Andererseits sehen Sie in der folgenden Grafik die kumulative Wahrscheinlichkeitsfunktion der Weibull-Verteilung anhand ihrer charakteristischen Werte.
Merkmale der Weibull-Verteilung
Die Weibull-Verteilung weist folgende Merkmale auf:
- Die Weibull-Verteilung hat zwei charakteristische Parameter, die ihren Graphen definieren: den Formparameter α und den Skalenparameter λ. Beide Parameter sind positive reelle Zahlen.
![\begin{array}{c}\alpha >0\\[2ex]\lambda >0\\[2ex]\text{Weibull}(\alpha,\lambda)\end{array}“ title=“Rendered by QuickLaTeX.com“ height=“92″ width=“101″ style=“vertical-align: 0px;“></p>
</p>
<ul>
<li> Die Weibull-Verteilung akzeptiert nur positive Abszissenwerte.</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-c8794febbd607514546841a325490654_l3.png)
![]()
- Der Mittelwert der Weibull-Verteilung wird mit der folgenden Formel berechnet:
![]()
- Andererseits lautet die Formel zum Ermitteln der Varianz der Weibull-Verteilung:
![]()
- Der Modus einer Zufallsvariablen, die einer Weibull-Verteilung mit α>1 folgt, kann durch den folgenden Ausdruck bestimmt werden:
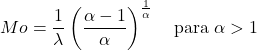
![]()
- Ebenso lautet die Formel für die kumulative Wahrscheinlichkeitsfunktion der Weibull-Verteilung:
![]()
- Der Asymmetriekoeffizient der Weibull-Verteilung wird durch Anwendung der folgenden Formel berechnet:
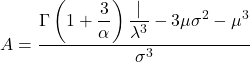
- Schließlich lautet die Formel, die es ermöglicht, den Kurtosis-Koeffizienten der Weibull-Verteilung zu bestimmen:
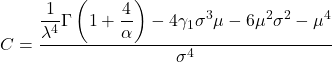
Gold
![]()
Anwendungen der Weibull-Verteilung
Die Weibull-Verteilung hat viele Anwendungen, darunter:
- In der angewandten Statistik wird die Weibull-Verteilung zur Überlebensanalyse verwendet.
- Im Ingenieurwesen wird die Weibull-Verteilung zur Modellierung von Funktionen im Zusammenhang mit der Fertigungszeit verwendet.
- In Radarsystemen zur Simulation der Streuung des empfangenen Signals.
- Im Versicherungsbereich zur Modellierung des Schadensumfangs.
- In der Meteorologie beispielsweise zur Modellierung der Häufigkeit unterschiedlicher Windgeschwindigkeiten.