So berechnen sie den vif in excel
Multikollinearität in der Regressionsanalyse tritt auf, wenn zwei oder mehr erklärende Variablen stark miteinander korrelieren, sodass sie im Regressionsmodell keine eindeutigen oder unabhängigen Informationen liefern. Wenn der Korrelationsgrad zwischen den Variablen hoch genug ist, kann dies zu Problemen bei der Anpassung und Interpretation des Regressionsmodells führen.
Glücklicherweise ist es möglich, Multikollinearität mithilfe einer Metrik namens Varianzinflationsfaktor (VIF) zu erkennen, die die Korrelation und Stärke der Korrelation zwischen erklärenden Variablen in einem Regressionsmodell misst.
In diesem Tutorial wird erläutert, wie Sie den VIF in Excel berechnen.
Beispiel: Berechnung des VIF in Excel
In diesem Beispiel führen wir eine multiple lineare Regression mit dem folgenden Datensatz durch, der die Attribute von 10 Basketballspielern beschreibt. Wir werden ein Regressionsmodell anpassen, das die Bewertung als Antwortvariable und Punkte, Assists und Rebounds als erklärende Variablen verwendet. Als nächstes identifizieren wir die VIF-Werte für jede erklärende Variable.
Schritt 1: Führen Sie eine multiple lineare Regression durch.
Gehen Sie im oberen Menüband zur Registerkarte „Daten“ und klicken Sie auf „Datenanalyse“. Wenn diese Option nicht angezeigt wird, müssen Sie zunächst die kostenlose Analysis ToolPak-Software installieren .

Sobald Sie auf Datenanalyse klicken, erscheint ein neues Fenster. Wählen Sie Regression und klicken Sie auf OK.

Füllen Sie die erforderlichen Tabellen für die Antwortvariablen und erklärenden Variablen aus und klicken Sie dann auf OK.
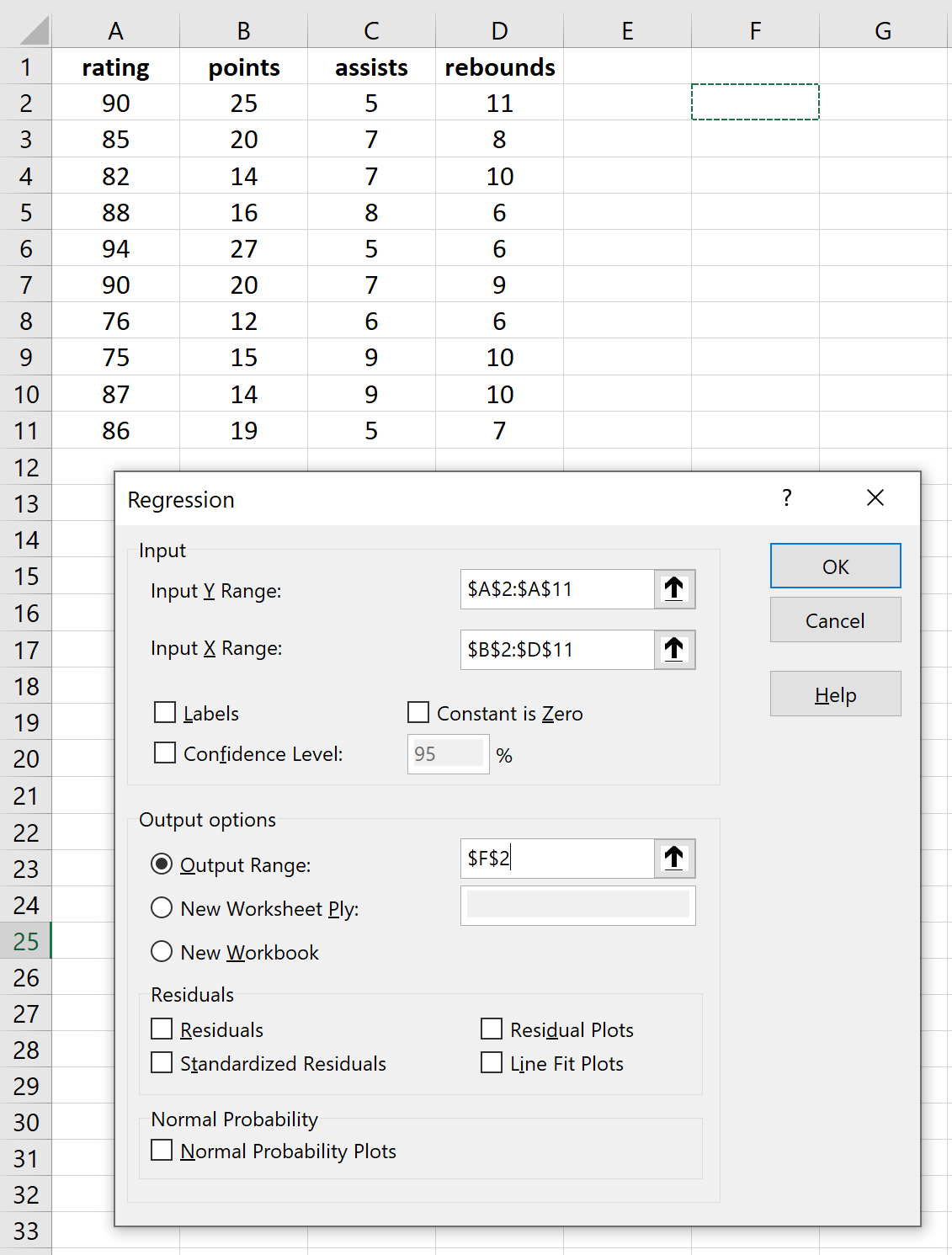
Dies führt zu folgendem Ergebnis:
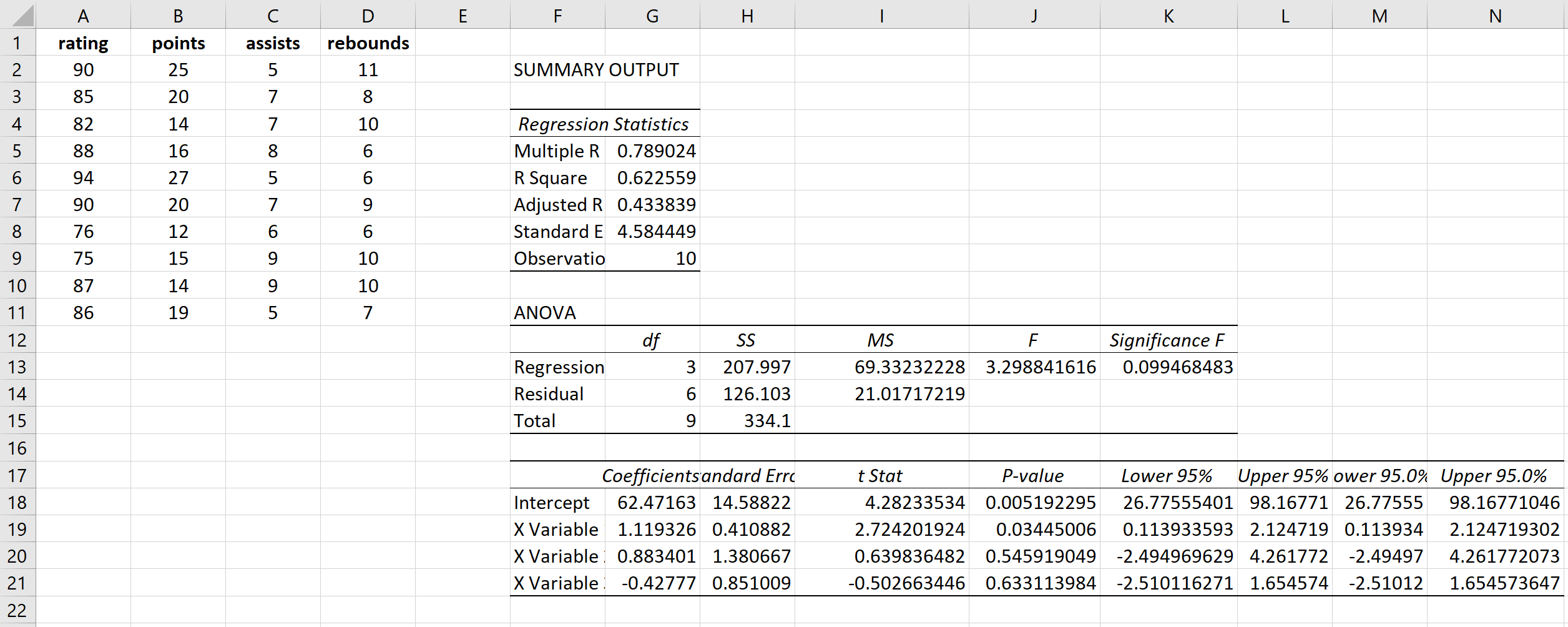
Schritt 2: Berechnen Sie den VIF für jede erklärende Variable.
Als nächstes können wir den VIF für jede der drei erklärenden Variablen berechnen, indem wir individuelle Regressionen durchführen, wobei wir eine erklärende Variable als Antwortvariable und die anderen beiden als erklärende Variablen verwenden.
Beispielsweise können wir den VIF für die Punktevariable berechnen, indem wir eine multiple lineare Regression durchführen, wobei wir Punkte als Antwortvariable und Assists und Rebounds als erklärende Variablen verwenden.
Dies führt zu folgendem Ergebnis:

Der VIF für Punkte wird wie folgt berechnet: 1 / (1 – R-Quadrat) = 1 / (1 – .433099) = 1,76 .
Wir können diesen Vorgang dann für die anderen beiden Variablen, Assists und Rebounds, wiederholen.
Es stellt sich heraus, dass die VIFs für die drei erklärenden Variablen wie folgt lauten:
Punkte: 1,76
Vorlagen: 1,96
Rebounds: 1,18
So interpretieren Sie VIF-Werte
Der VIF-Wert beginnt bei 1 und hat keine Obergrenze. Eine allgemeine Regel für die Interpretation von VIFs lautet:
- Ein Wert von 1 gibt an, dass keine Korrelation zwischen einer bestimmten erklärenden Variablen und einer anderen erklärenden Variablen im Modell besteht.
- Ein Wert zwischen 1 und 5 weist auf eine mäßige Korrelation zwischen einer bestimmten erklärenden Variablen und anderen erklärenden Variablen im Modell hin, ist jedoch oft nicht schwerwiegend genug, um besondere Aufmerksamkeit zu erfordern.
- Ein Wert größer als 5 weist auf eine potenziell schwerwiegende Korrelation zwischen einer bestimmten erklärenden Variablen und anderen erklärenden Variablen im Modell hin. In diesem Fall sind die Koeffizientenschätzungen und p-Werte in den Regressionsergebnissen wahrscheinlich unzuverlässig.
Da jeder der VIF-Werte der erklärenden Variablen in unserem Regressionsmodell nahe bei 1 liegt, ist Multikollinearität in unserem Beispiel kein Problem.