So interpretieren sie den reststandardfehler

Der Reststandardfehler wird verwendet, um zu messen, wie gut ein Regressionsmodell zu einem Datensatz passt.

Vereinfacht ausgedrückt misst es die Standardabweichung der Residuen in einem Regressionsmodell.

Es wird wie folgt berechnet:

Reststandardfehler = √ Σ(y – ŷ) ² /df

Gold:

• y: Der beobachtete Wert
• ŷ: Der vorhergesagte Wert
• df: Die Freiheitsgrade, berechnet als Gesamtzahl der Beobachtungen – Gesamtzahl der Modellparameter.

Je kleiner der Reststandardfehler ist, desto besser passt ein Regressionsmodell an einen Datensatz. Umgekehrt gilt: Je höher der Reststandardfehler, desto schlechter passt das Regressionsmodell an einen Datensatz.

Bei einem Regressionsmodell mit einem kleinen Reststandardfehler sind die Datenpunkte eng um die angepasste Regressionslinie gruppiert:

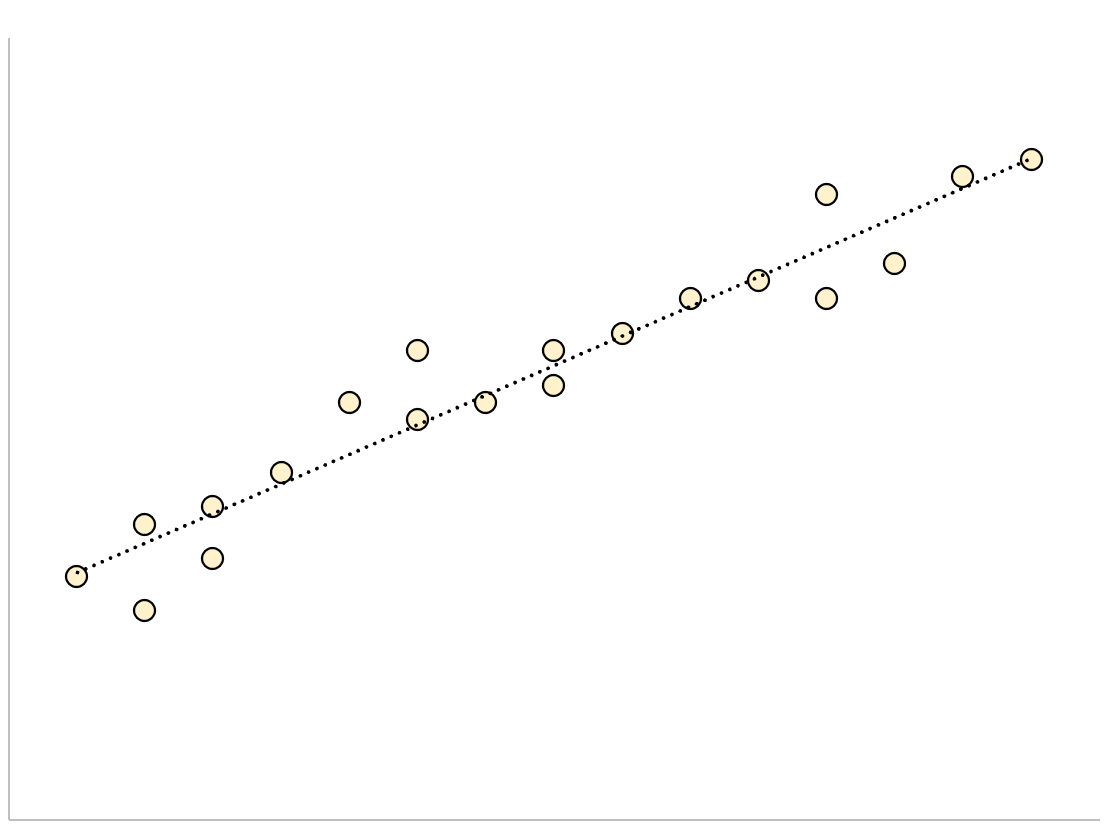
Die Residuen dieses Modells (die Differenz zwischen den beobachteten Werten und den vorhergesagten Werten) werden klein sein, was bedeutet, dass auch der verbleibende Standardfehler klein sein wird.

Umgekehrt sind die Datenpunkte eines Regressionsmodells mit einem großen Reststandardfehler lockerer um die angepasste Regressionslinie verteilt:

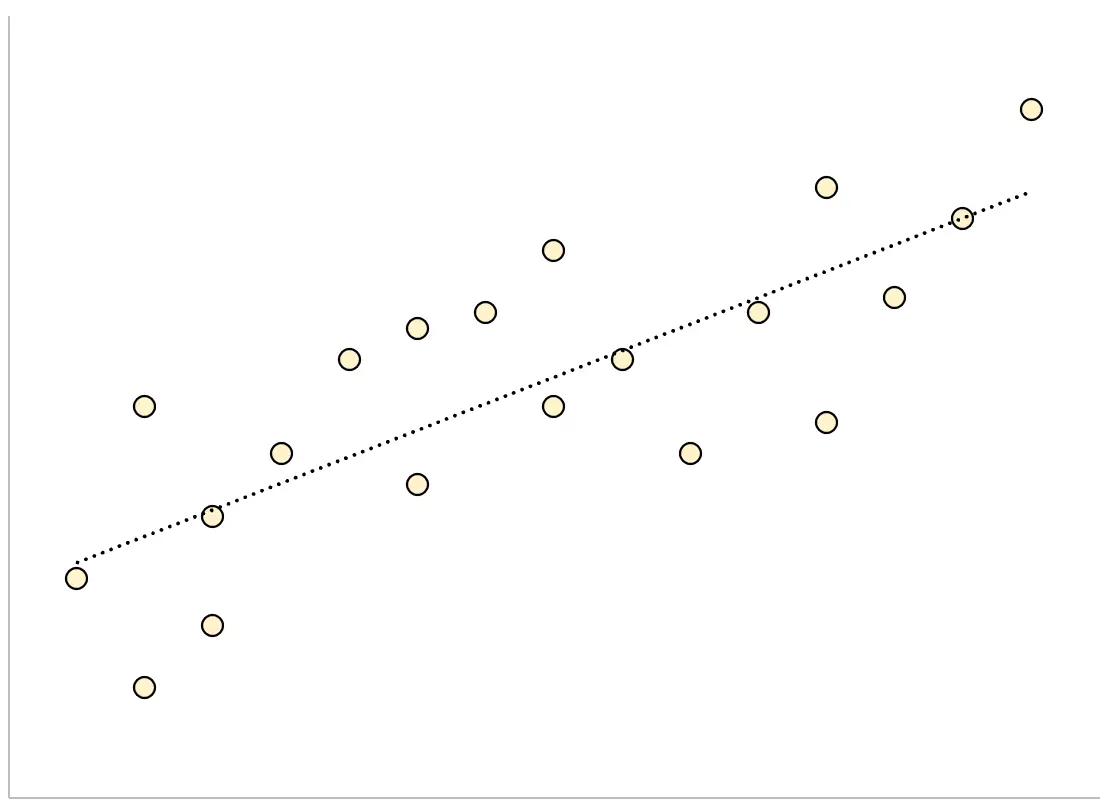
Die Residuen dieses Modells werden größer sein, was bedeutet, dass auch der Reststandardfehler größer sein wird.

Das folgende Beispiel zeigt, wie der Reststandardfehler eines Regressionsmodells in R berechnet und interpretiert wird.

Beispiel: Interpretation des Reststandardfehlers

Angenommen, wir möchten das folgende multiple lineare Regressionsmodell anpassen:

mpg = β ₀ + β ₁ (Hubraum) + β ₂ (Leistung)

Dieses Modell verwendet die Prädiktorvariablen „Hubraum“ und „PS“, um die Meilen pro Gallone vorherzusagen, die ein bestimmtes Auto zurücklegt.

Der folgende Code zeigt, wie dieses Regressionsmodell in R angepasst wird:

 #load built-in mtcars dataset
data(mtcars)

#fit regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Call:
lm(formula = mpg ~ disp + hp, data = mtcars)

Residuals:
    Min 1Q Median 3Q Max 
-4.7945 -2.3036 -0.8246 1.8582 6.9363 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

Am unteren Rand des Ergebnisses können wir sehen, dass der verbleibende Standardfehler dieses Modells 3,127 beträgt.

Dies zeigt uns, dass das Regressionsmodell Auto-MPG mit einem durchschnittlichen Fehler von etwa 3.127 vorhersagt.

Verwenden des Reststandardfehlers zum Vergleichen von Modellen

Der Reststandardfehler ist besonders nützlich, um die Anpassung verschiedener Regressionsmodelle zu vergleichen.

Angenommen, wir passen zwei verschiedene Regressionsmodelle an, um den Auto-MPG vorherzusagen. Der verbleibende Standardfehler jedes Modells ist wie folgt:

• Reststandardfehler von Modell 1: 3,127
• Reststandardfehler von Modell 2: 5,657

Da Modell 1 einen geringeren Reststandardfehler aufweist, passt es besser zu den Daten als Modell 2. Daher würden wir es vorziehen, Modell 1 zur Vorhersage von Auto-MPG zu verwenden, da die Vorhersagen, die es macht, näher an den beobachteten MPG-Werten von Autos liegen.

Zusätzliche Ressourcen

So führen Sie eine einfache lineare Regression in R durch
So führen Sie eine multiple lineare Regression in R durch
So erstellen Sie ein Residuendiagramm in R