So lesen sie die chi-quadrat-verteilungstabelle

In diesem Tutorial wird erklärt, wie man das Chi-Quadrat-Verteilungsdiagramm liest und interpretiert.

Was ist die Chi-Quadrat-Verteilungstabelle?

Die Chi-Quadrat- Verteilungstabelle ist eine Tabelle, die die kritischen Werte der Chi-Quadrat-Verteilung zeigt. Um die Chi-Quadrat-Verteilungstabelle verwenden zu können, müssen Sie nur zwei Werte kennen:

• Freiheitsgrade für den Chi-Quadrat-Test
• Das Alpha-Level des Tests (übliche Optionen sind 0,01, 0,05 und 0,10)

Das folgende Bild zeigt die ersten 20 Zeilen der Chi-Quadrat-Verteilungstabelle mit Freiheitsgraden auf der linken Seite der Tabelle und Alpha-Ebenen oben in der Tabelle:

Hinweis: Eine vollständige Chi-Quadrat-Verteilungstabelle mit mehr Freiheitsgraden finden Sie hier.

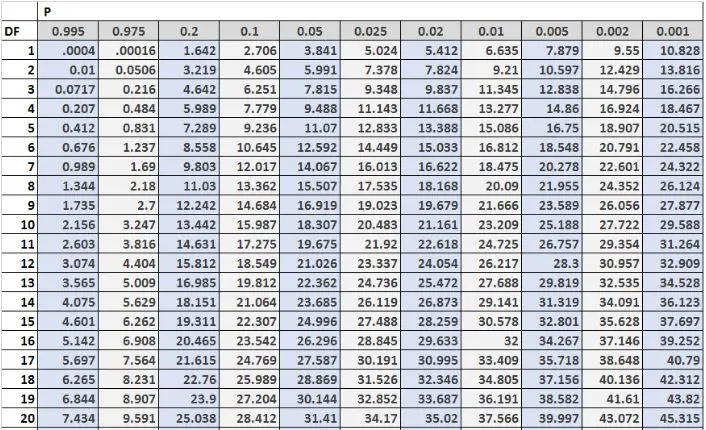
Die kritischen Werte in der Tabelle werden häufig mit der Teststatistik eines Chi-Quadrat-Tests verglichen. Wenn die Teststatistik größer als der in der Tabelle gefundene kritische Wert ist, können Sie die Nullhypothese des Chi-Quadrat-Tests ablehnen und daraus schließen, dass die Testergebnisse statistisch signifikant sind.

Beispiele für die Verwendung der Chi-Quadrat-Verteilungstabelle

Wir zeigen, wie Sie die Chi-Quadrat-Verteilungstabelle mit den folgenden drei Arten von Chi-Quadrat-Tests verwenden:

• Chi-Quadrat-Test für Unabhängigkeit
• Chi-Quadrat-Test für die Güte der Anpassung
• Chi-Quadrat-Test für Homogenität

Chi-Quadrat-Test für Unabhängigkeit

Wir verwenden einen Chi-Quadrat-Test zur Unabhängigkeit, wenn wir testen möchten, ob zwischen zwei kategorialen Variablen ein signifikanter Zusammenhang besteht oder nicht.

Beispiel: Angenommen, wir möchten wissen, ob das Geschlecht mit der Präferenz für eine politische Partei zusammenhängt. Wir nehmen eine einfache Zufallsstichprobe von 500 Wählern und befragen sie zu ihrer politischen Parteipräferenz. Mit einem Signifikanzniveau von 0,05 führen wir einen Chi-Quadrat-Test durch, um festzustellen, ob das Geschlecht mit der Präferenz für eine politische Partei zusammenhängt. Die folgende Tabelle stellt die Ergebnisse der Umfrage dar:

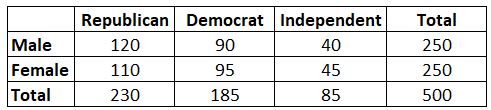
Es stellt sich heraus, dass die Teststatistik für diesen Chi-Quadrat-Test 0,864 beträgt.

Dann können wir den kritischen Testwert in der Chi-Quadrat-Verteilungstabelle finden. Die Freiheitsgrade sind gleich (#Zeilen-1) * (#Spalten-1) = (2-1) * (3-1) = 2 und das Problem sagte uns, dass wir einen Alpha-Wert von 0,05 verwenden sollten. Also, Gemäß der Chi-Quadrat-Verteilungstabelle beträgt der kritische Wert des Tests 5,991 .

Da unsere Teststatistik unter unserem kritischen Wert liegt, können wir die Nullhypothese nicht ablehnen. Das bedeutet, dass uns keine ausreichenden Belege dafür vorliegen, dass ein Zusammenhang zwischen Geschlecht und politischen Parteipräferenzen besteht.

Chi-Quadrat-Test für die Güte der Anpassung

Wir verwenden einen Chi-Quadrat -Anpassungstest, wenn wir testen möchten, ob eine kategoriale Variable einer hypothetischen Verteilung folgt oder nicht.

Beispiel: Ein Ladenbesitzer sagt, dass 30 % aller seiner Wochenendkunden am Freitag kommen, 50 % am Samstag und 20 % am Sonntag. Ein unabhängiger Forscher besucht das Geschäft an einem zufälligen Wochenende und findet am Freitag 91 Kunden, am Samstag 104 und am Sonntag 65. Mit einem Signifikanzniveau von 0,10 führen wir einen Chi-Quadrat-Test durch, um die Anpassungsgüte zu überprüfen und festzustellen, ob die Daten mit der Behauptung des Ladenbesitzers übereinstimmen.

In diesem Fall beträgt die Teststatistik 10.616.

Dann können wir den kritischen Testwert in der Chi-Quadrat-Verteilungstabelle finden. Die Freiheitsgrade sind gleich (#outcomes-1) = 3-1 = 2 und das Problem sagt uns, dass wir einen Alpha-Wert von 0,10 verwenden sollten. Gemäß der Chi-Quadrat-Verteilungstabelle beträgt der kritische Wert des Tests also 4,605 .

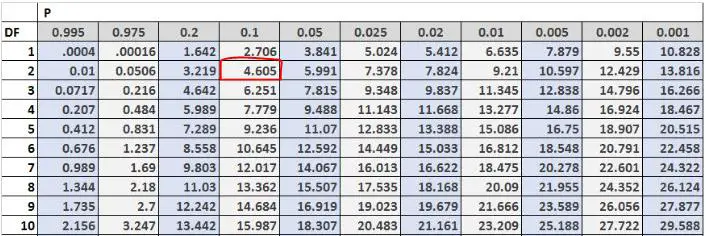
Da unsere Teststatistik größer als unser kritischer Wert ist, lehnen wir die Nullhypothese ab. Das bedeutet, dass wir genügend Beweise dafür haben, dass die tatsächliche Verteilung der Kunden, die am Wochenende in dieses Geschäft kommen, nicht 30 % am Freitag, 50 % am Samstag und 20 % am Sonntag beträgt.

Chi-Quadrat-Test für Homogenität

Wir verwenden einen Chi-Quadrat-Test zur Homogenität, wenn wir formal testen möchten, ob es einen Unterschied in den Proportionen zwischen mehreren Gruppen gibt oder nicht.

Beispiel: Ein Basketball-Trainingszentrum möchte herausfinden, ob zwei neue Trainingsprogramme den Anteil seiner Spieler verbessern, die eine schwierige Schießprüfung bestehen. 172 Spieler werden zufällig dem Programm 1, 173 dem Programm 2 und 215 dem aktuellen Programm zugewiesen. Nachdem die Spieler die Trainingsprogramme einen Monat lang genutzt haben, absolvieren sie anschließend einen Schießtest. Die folgende Tabelle zeigt die Anzahl der Spieler, die den Schießtest bestehen, basierend auf dem von ihnen verwendeten Programm.

Mit einem Signifikanzniveau von 0,05 führen wir einen Chi-Quadrat-Test durch, um festzustellen, ob die Erfolgsquote für jedes Trainingsprogramm gleich ist.

Es stellt sich heraus, dass die Teststatistik für diesen Chi-Quadrat-Test 4,208 beträgt.

Dann können wir den kritischen Testwert in der Chi-Quadrat-Verteilungstabelle finden. Die Freiheitsgrade sind gleich (#Zeilen-1) * (#Spalten-1) = (2-1) * (3-1) = 2 und das Problem sagte uns, dass wir einen Alpha-Wert von 0,05 verwenden sollten. Also, Gemäß der Chi-Quadrat-Verteilungstabelle beträgt der kritische Wert des Tests 5,991 .

Da unsere Teststatistik unter unserem kritischen Wert liegt, können wir die Nullhypothese nicht ablehnen. Das bedeutet, dass uns keine ausreichenden Beweise dafür vorliegen, dass die drei Trainingsprogramme unterschiedliche Ergebnisse liefern.