So lesen sie eine kovarianzmatrix

Kovarianz ist ein Maß dafür, wie Änderungen einer Variablen mit Änderungen einer zweiten Variablen verbunden sind. Genauer gesagt ist es ein Maß für den Grad, in dem zwei Variablen linear miteinander verbunden sind.

Eine Kovarianzmatrix ist eine quadratische Matrix, die die Kovarianz zwischen vielen verschiedenen Variablen zeigt. Dies kann eine nützliche Methode sein, um zu verstehen, wie verschiedene Variablen in einem Datensatz zusammenhängen.

Das folgende Beispiel zeigt, wie man eine Kovarianzmatrix in der Praxis liest.

So lesen Sie eine Kovarianzmatrix

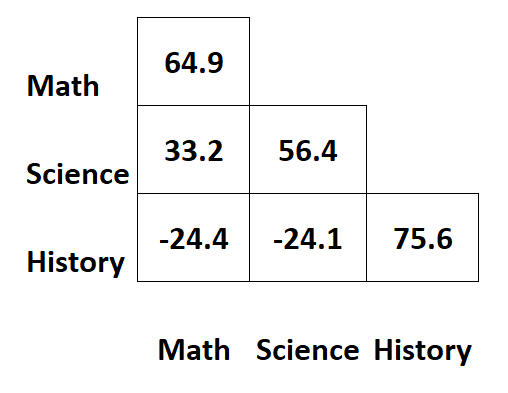
Angenommen, wir haben die folgende Kovarianzmatrix, die Informationen über Prüfungsergebnisse für drei verschiedene Fächer für Studenten enthält:

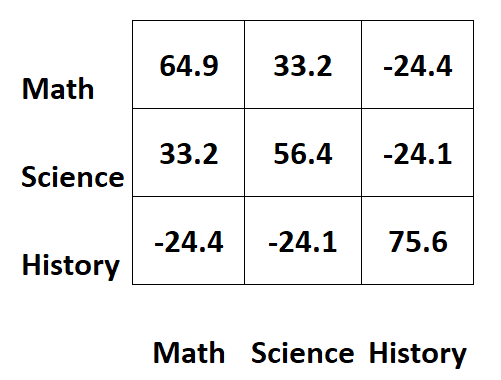
Die Werte entlang der Diagonalen der Matrix stellen die Varianzen jedes Subjekts dar.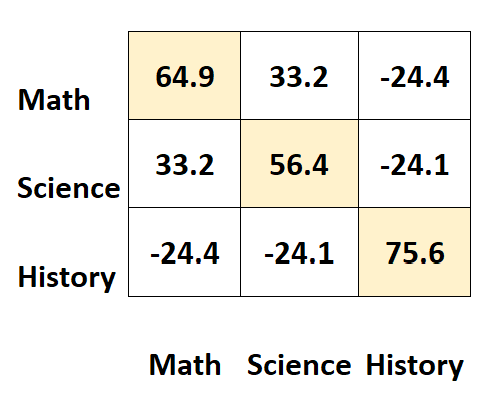

Zum Beispiel:

• Die Varianz der Mathematikergebnisse beträgt 64,9 .
• Die Varianz der naturwissenschaftlichen Ergebnisse beträgt 56,4 .
• Die Varianz der historischen Werte beträgt 75,6 .

Die anderen Werte der Matrix stellen die Kovarianzen zwischen den verschiedenen Subjekten dar.

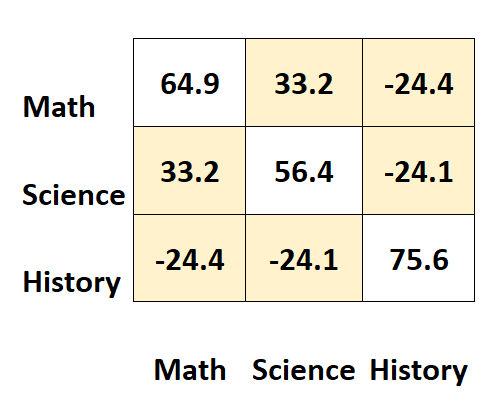
Zum Beispiel:

• Die Kovarianz zwischen den Ergebnissen in Mathematik und Naturwissenschaften beträgt 33,2 .
• Die Kovarianz zwischen Mathematik- und Geschichtsergebnissen beträgt –24,4 .
• Die Kovarianz zwischen den Ergebnissen in Naturwissenschaften und Geschichte beträgt –24,1 .

Eine positive Zahl für die Kovarianz zeigt an, dass zwei Variablen tendenziell gleichzeitig zunehmen oder abnehmen.

Beispielsweise weisen Mathematik und Naturwissenschaften eine positive Kovarianz auf ( 33,2 ), was darauf hinweist, dass Schüler, die in Mathematik gute Ergebnisse erzielen, tendenziell auch in Naturwissenschaften gute Ergebnisse erzielen.

Umgekehrt schneiden Schüler, die in Mathematik schlecht abschneiden, tendenziell auch in den Naturwissenschaften schlecht ab.

Eine negative Zahl für die Kovarianz bedeutet, dass eine zweite Variable tendenziell abnimmt, wenn eine Variable zunimmt.

Beispielsweise haben Mathematik und Geschichte eine negative Kovarianz ( -24,44 ), was darauf hindeutet, dass Schüler, die in Mathematik gute Leistungen erbringen, tendenziell schlechte Leistungen in Geschichte erbringen.

Umgekehrt erzielen Schüler, die in Mathematik schlecht abschneiden, tendenziell gute Ergebnisse in Geschichte.

Eine Anmerkung zur Symmetrie einer Kovarianzmatrix

Es ist zu beachten, dass eine Kovarianzmatrix vollkommen symmetrisch ist.

Beispielsweise zeigt die Zelle oben rechts genau den gleichen Wert wie die Zelle unten links:

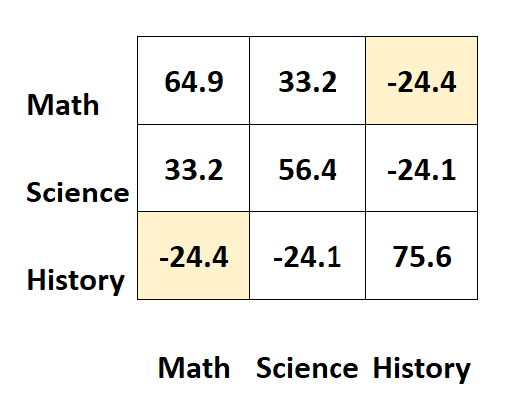
Tatsächlich messen die beiden Zellen die Kovarianz zwischen Geschichte und Mathematik.

Da eine Kovarianzmatrix symmetrisch ist, ist die Hälfte der in der Matrix angezeigten Kovarianzwerte redundant und unnötig.

Daher wird manchmal nur die Hälfte der Kovarianzmatrix angezeigt:

Wann ist eine Kovarianzmatrix zu verwenden?

In der Praxis müssen Sie häufig häufiger eine Korrelationsmatrix erstellen und interpretieren als eine Kovarianzmatrix.

Kovarianzmatrizen werden jedoch häufig „unter der Haube“ für verschiedene Algorithmen und Modelle des maschinellen Lernens verwendet.

Die Kovarianzmatrix wird beispielsweise bei der Hauptkomponentenanalyse verwendet und hilft uns, die zugrunde liegenden Muster in einem Datensatz mit einer großen Anzahl von Variablen zu verstehen.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie mit unterschiedlicher Statistiksoftware eine Kovarianzmatrix erstellen:

So erstellen Sie eine Kovarianzmatrix in R
So erstellen Sie eine Kovarianzmatrix in Python
So erstellen Sie eine Kovarianzmatrix in SPSS
So erstellen Sie eine Kovarianzmatrix in Excel