Verwendung der z-tabelle (mit beispielen)

Eine Z-Tabelle ist eine Tabelle, die Ihnen sagt, wie viel Prozent der Werte in einer Standardnormalverteilung unter einen bestimmten Z-Wert fallen.

Ein Z-Score sagt Ihnen einfach, um wie viele Standardabweichungen ein einzelner Datenwert vom Mittelwert abweicht. Es wird wie folgt berechnet:

Z-Score = (x – μ) / σ

Gold:

• x: individueller Datenwert
• μ: Bevölkerungsdurchschnitt
• σ: Populationsstandardabweichung

Dieses Tutorial zeigt mehrere Beispiele für die Verwendung der Z-Tabelle.

Beispiel 1

Die Ergebnisse einer bestimmten Hochschulaufnahmeprüfung sind normalverteilt mit dem Mittelwert μ = 82 und der Standardabweichung σ = 8. Ungefähr wie viel Prozent der Studenten erreichen bei der Prüfung weniger als 84 Punkte?

Schritt 1: Finden Sie den Z-Score.

Zuerst ermitteln wir den Z-Score, der einem Prüfungsergebnis von 84 zugeordnet ist:

z-Score = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0,25

Schritt 2: Verwenden Sie das Z-Diagramm, um den Prozentsatz zu ermitteln, der dem Z-Score entspricht.

Als nächstes suchen wir in der Z-Tabelle nach dem Wert 0,25 :

Rund 59,87 % der Studierenden erzielen in dieser Prüfung eine Punktzahl unter 84.

Beispiel 2

Die Höhe der Pflanzen in einem bestimmten Garten ist normal verteilt mit einem Mittelwert von μ = 26,5 Zoll und einer Standardabweichung von σ = 2,5 Zoll. Wie viel Prozent der Pflanzen sind ungefähr über 26 Zoll groß?

Schritt 1: Finden Sie den Z-Score.

Zuerst ermitteln wir den Z-Score, der einer Körpergröße von 26 Zoll zugeordnet ist.

z-Score = (x – μ) / σ = (26 – 26,5) / 2,5 = -0,5 / 2,5 = -0,2

Schritt 2: Verwenden Sie das Z-Diagramm, um den Prozentsatz zu ermitteln, der dem Z-Score entspricht.

Als nächstes suchen wir nach dem Wert -0,2   in Tabelle z:

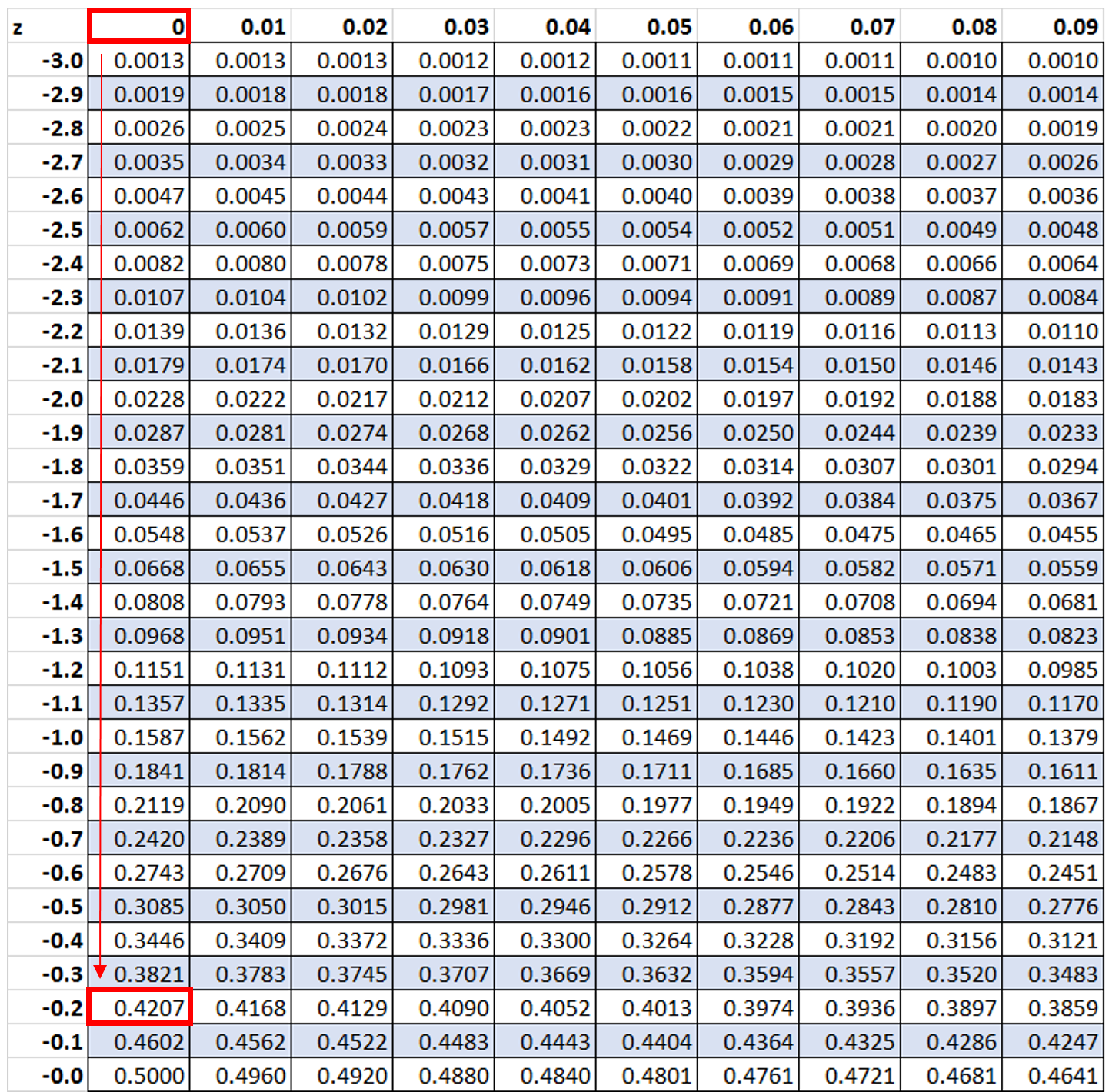
Wir sehen, dass 42,07 % der Werte unter einem Z-Score von -0,2 liegen. In diesem Beispiel möchten wir jedoch wissen, wie viel Prozent der Werte größer als -0,2 sind, was wir mit der Formel 100 % – 42,07 % = 57,93 % ermitteln können.

Ungefähr 59,87 % der Pflanzen in diesem Garten sind also über 26 Zoll hoch.

Beispiel 3

Das Gewicht einer bestimmten Delfinart ist normalverteilt mit einem Mittelwert von μ = 400 Pfund und einer Standardabweichung von σ = 25 Pfund. Wie viel Prozent der Delfine wiegen ungefähr zwischen 410 und 425 Pfund?

Schritt 1: Finden Sie die Z-Scores.

Zunächst ermitteln wir die Z-Scores für 410 Bücher und 425 Bücher

Z-Score von 410 = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0,4

z-Score von 425 = (x – μ) / σ = (425 – 400) / 25 = 25 / 25 = 1

Schritt 2: Verwenden Sie das Z-Diagramm, um die Prozentsätze zu ermitteln, die jedem Z-Wert entsprechen.

Zuerst suchen wir nach dem Wert 0,4   in Tabelle z:

Als nächstes suchen wir nach dem Wert 1   in Tabelle z:

Zum Schluss subtrahieren wir den kleinsten Wert vom größten Wert: 0,8413 – 0,6554 = 0,1859 .

So wiegen etwa 18,59 % der Delfine zwischen 410 und 425 Pfund.

Zusätzliche Ressourcen

Eine Einführung in die Normalverteilung
Normalverteilungsgebietsrechner
Z-Score-Rechner