So lesen sie ein halblogarithmisches diagramm: mit beispielen

Ein halblogarithmisches Diagramm ist ein Diagrammtyp, der eine lineare Skala auf der x-Achse und eine logarithmische Skala auf der y-Achse verwendet.

Wir verwenden diesen Diagrammtyp häufig, wenn die Werte der y-Variablen eine viel größere Variabilität aufweisen als die Werte der x-Variablen.

Diese Art von Diagramm eignet sich besonders zur Visualisierung der prozentualen Änderung einer Variablen im Zeitverlauf.

Die folgenden Beispiele zeigen, wie man halblogarithmische Graphen in der Praxis liest.

Beispiel 1: Halblogarithmisches Diagramm für das Pflanzenwachstum

Nehmen wir an, ein Biologe möchte ein Liniendiagramm erstellen, um das Wachstum einer bestimmten Pflanze über einen Zeitraum von 20 Wochen zu visualisieren.

Zunächst wird das folgende Liniendiagramm mit einer linearen Skala auf der y-Achse erstellt:

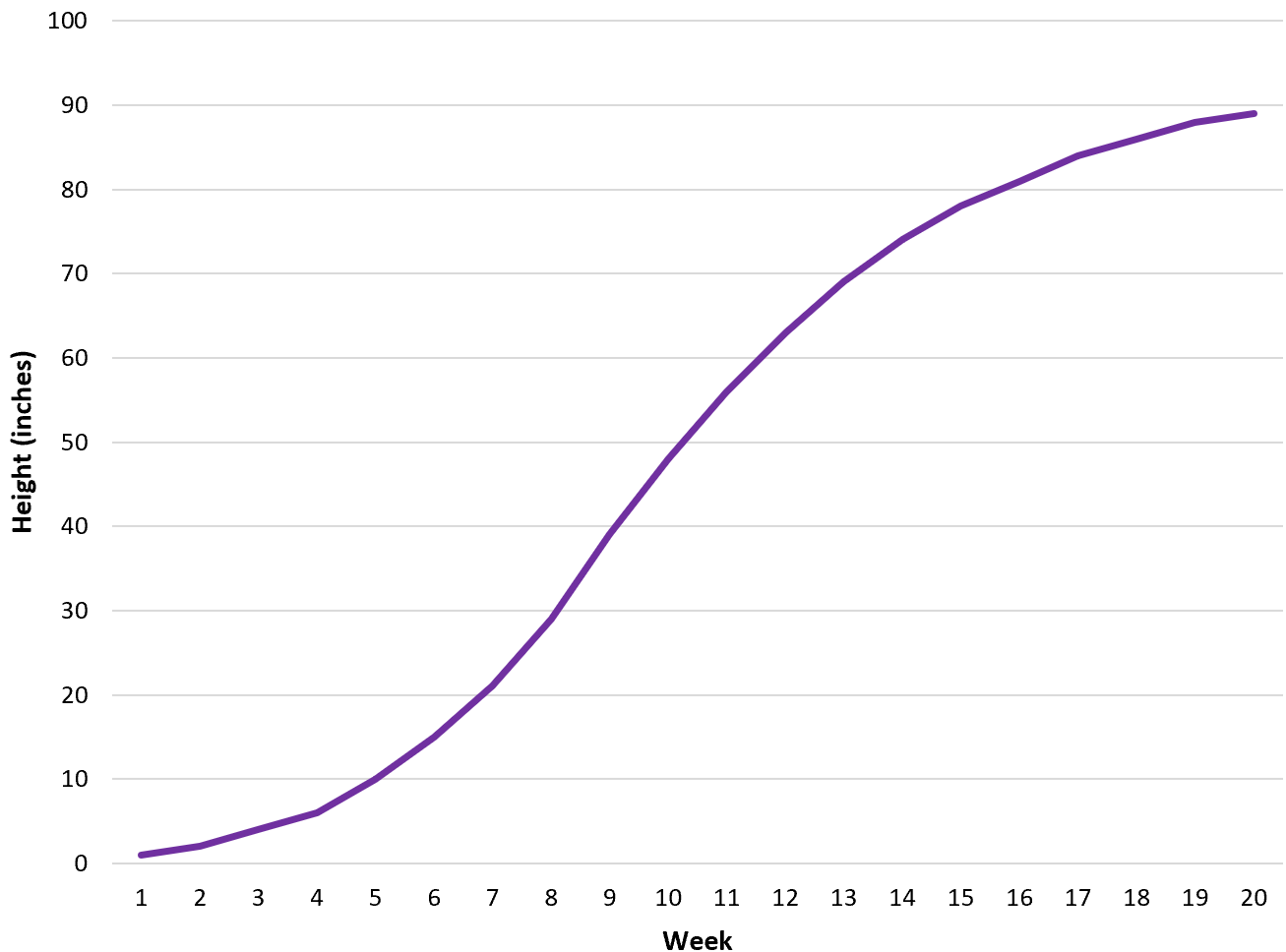
Dieses Diagramm eignet sich zur Visualisierung der groben Veränderung der Pflanzenhöhe von einer Woche zur nächsten.

Sie kann jedoch ein halblogarithmisches Diagramm verwenden, um die prozentuale Änderung der Pflanzenhöhe von Woche zu Woche einfacher zu visualisieren:

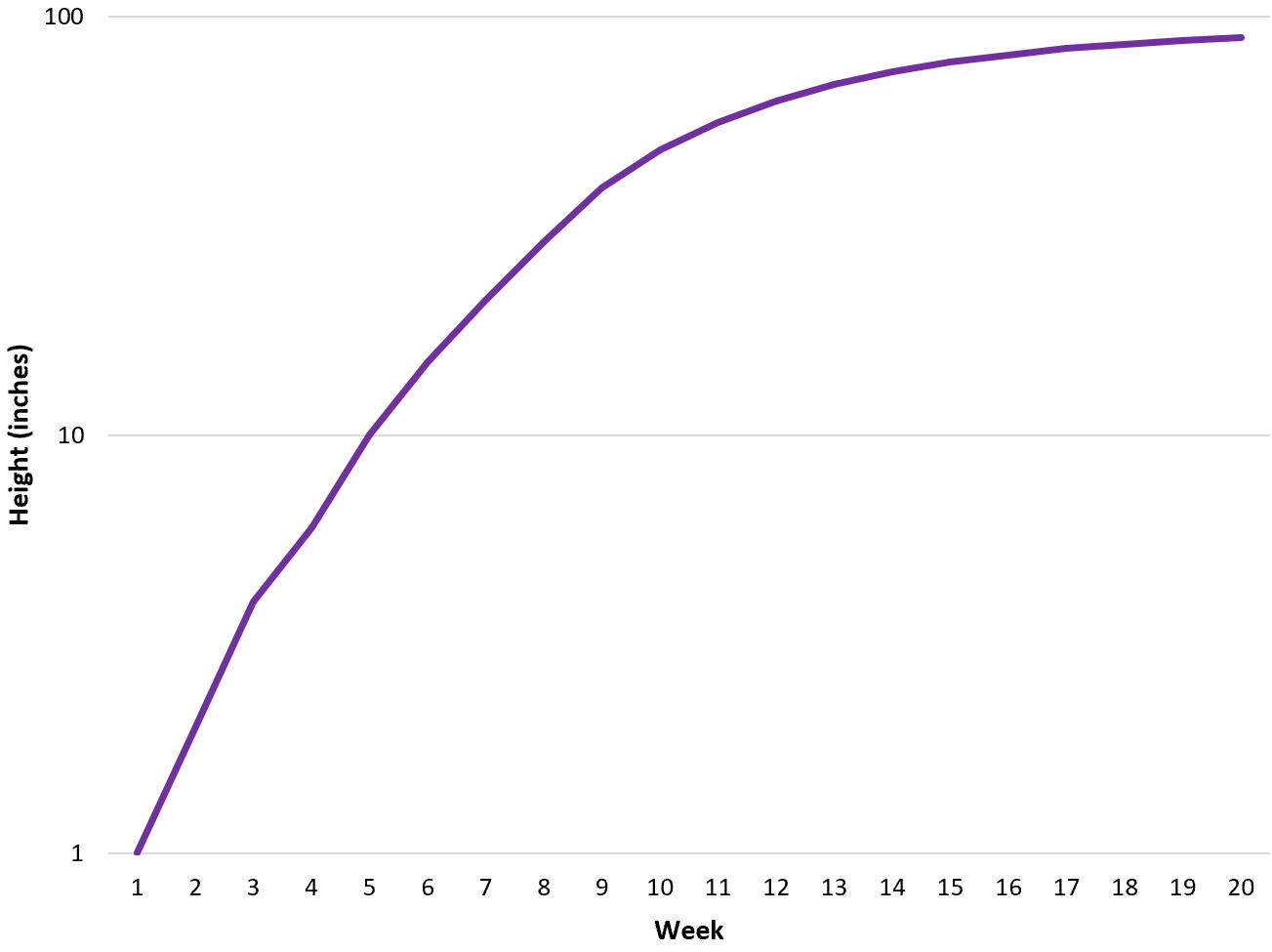
Beachten Sie, dass die Y-Achse im logarithmischen Maßstab gemessen wird.

Anhand dieser Grafik können wir erkennen, dass der Wachstumsprozentsatz der Pflanze in den ersten Wochen am schnellsten ist und sich dann in den letzten Wochen deutlich verlangsamt.

Beispiel 2: Halblogarithmisches Diagramm für das Investitionswachstum

Nehmen wir an, ein Investor möchte ein Liniendiagramm erstellen, um das Wachstum einer bestimmten Investition über einen Zeitraum von 30 Jahren zu visualisieren.

Zunächst wird das folgende Liniendiagramm mit einer linearen Skala auf der y-Achse erstellt:

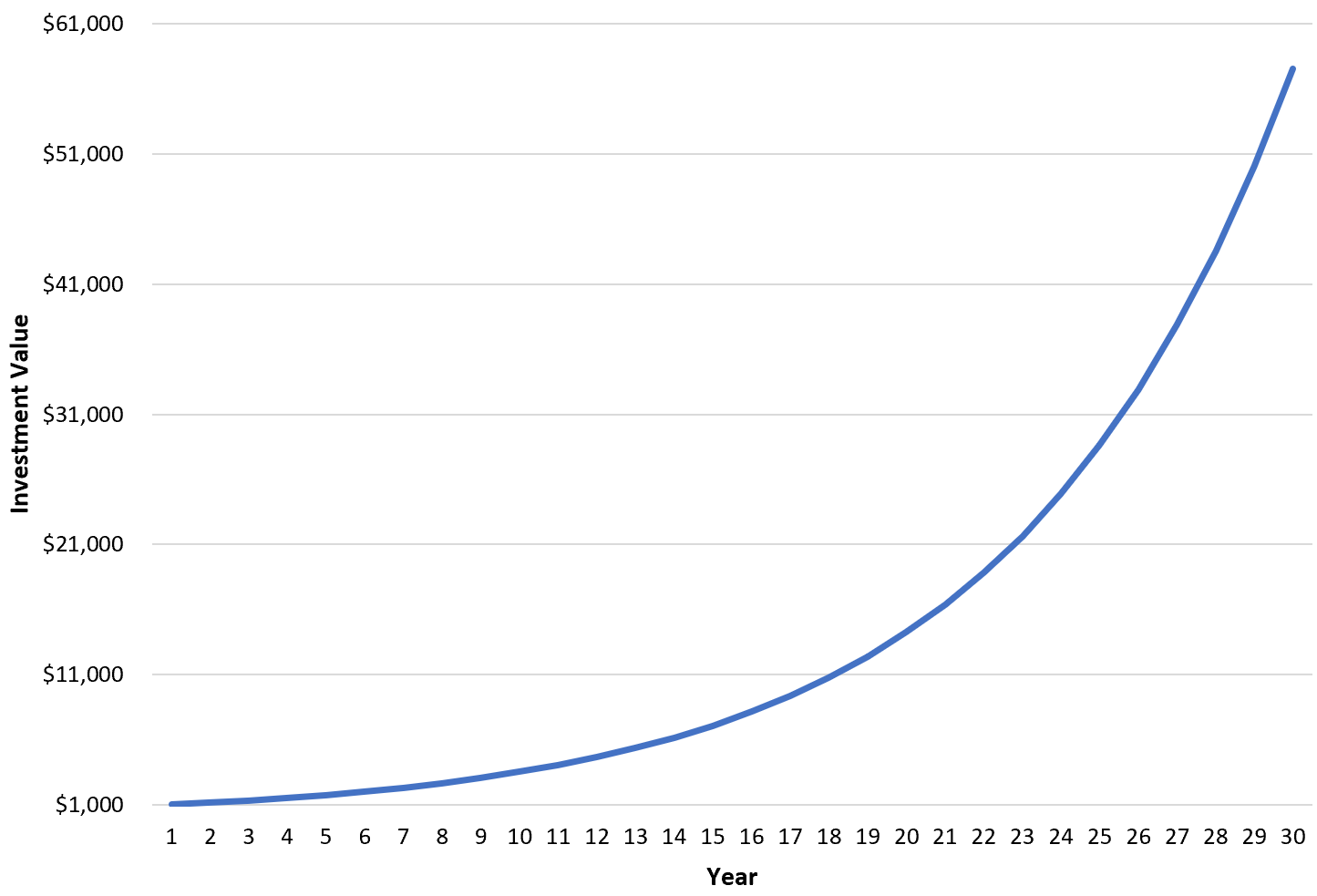
Dieses Diagramm eignet sich zur Visualisierung der Bruttowertveränderung der Investition von einem Jahr zum nächsten.

Allerdings kann ein halblogarithmisches Diagramm verwendet werden, um die prozentuale Veränderung des Anlagewerts von Jahr zu Jahr einfacher zu visualisieren:

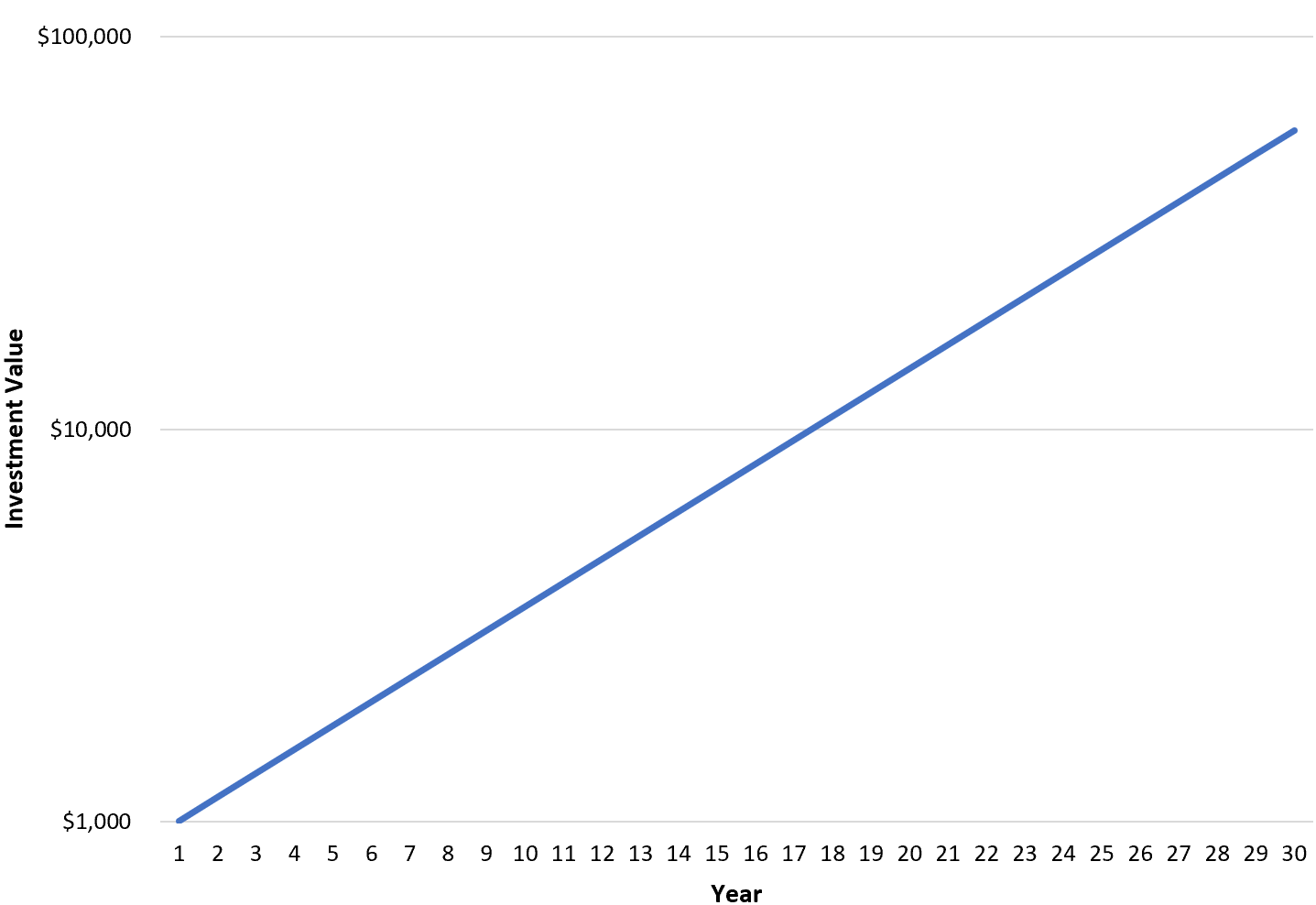
Beachten Sie, dass die Y-Achse im logarithmischen Maßstab gemessen wird.

Anhand dieses Diagramms können wir erkennen, dass der Prozentsatz des Investitionswachstums tatsächlich von Jahr zu Jahr konstant ist.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zur Verwendung logarithmischer Skalen in Diagrammen:

So erstellen Sie ein Semi-Log-Diagramm in Excel
Wann sollten Sie in Diagrammen eine logarithmische Skala verwenden?