So interpretieren sie den quadratischen mittelwertfehler (rmse)

Die Regressionsanalyse ist eine Technik, mit der wir die Beziehung zwischen einer oder mehreren Prädiktorvariablen und einer Antwortvariablen verstehen können.

Eine Möglichkeit zu bewerten, wie gut ein Regressionsmodell zu einem Datensatz passt, besteht darin, den mittleren quadratischen Fehler zu berechnen, eine Metrik, die uns den durchschnittlichen Abstand zwischen den vorhergesagten Werten des Modells und den tatsächlichen Werten des Datensatzes angibt.

Je niedriger der RMSE, desto besser kann ein bestimmtes Modell einen Datensatz „anpassen“.

Die Formel zum Ermitteln des mittleren quadratischen Fehlers, oft als RMSE abgekürzt, lautet:

RMSE = √ Σ(P _i – O _i ) ² / n

Gold:

• Σ ist ein ausgefallenes Symbol, das „Summe“ bedeutet
• P _i ist der vorhergesagte Wert für die ^i-te Beobachtung im Datensatz
• O _i ist der beobachtete Wert für die ^i-te Beobachtung im Datensatz
• n ist die Stichprobengröße

Das folgende Beispiel zeigt, wie der RMSE für ein bestimmtes Regressionsmodell interpretiert wird.

Beispiel: So interpretieren Sie RMSE für ein Regressionsmodell

Angenommen, wir möchten ein Regressionsmodell erstellen, das „Studienstunden“ verwendet, um die „Prüfungsnote“ der Studierenden bei einer bestimmten Hochschulaufnahmeprüfung vorherzusagen.

Für 15 Studierende erheben wir folgende Daten:

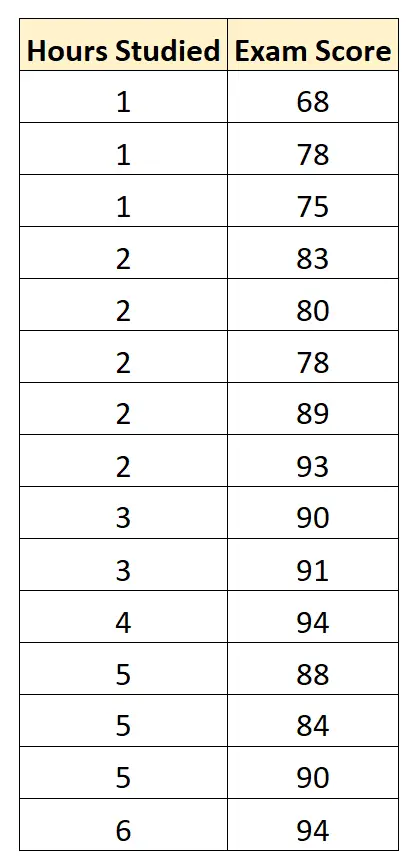
Wir verwenden dann Statistiksoftware (wie Excel, SPSS, R, Python) usw. um das folgende angepasste Regressionsmodell zu finden:

Prüfungsergebnis = 75,95 + 3,08* (Studienstunden)

Mithilfe dieser Gleichung können wir dann die Prüfungsergebnisse jedes Schülers vorhersagen, basierend auf der Anzahl der Stunden, die er gelernt hat:

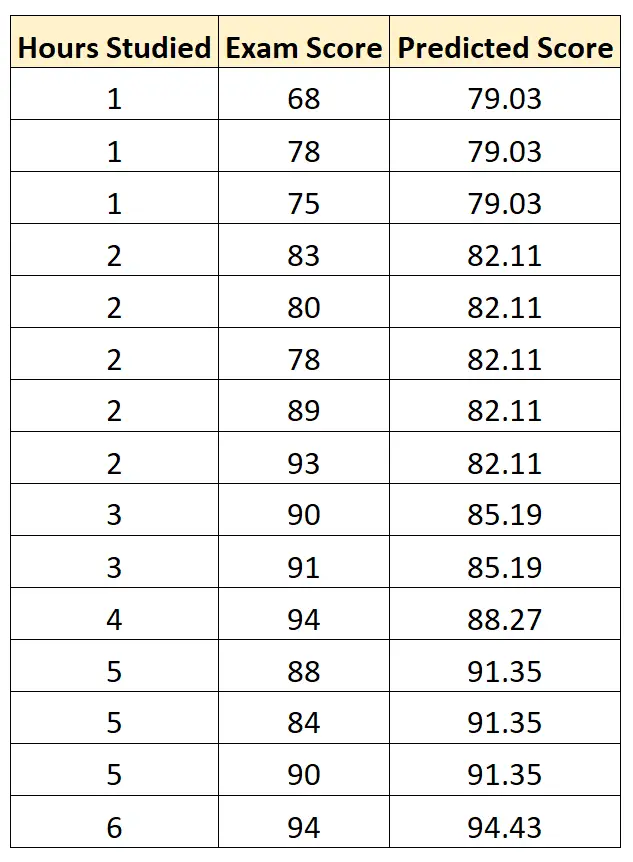
Anschließend können wir die quadrierte Differenz zwischen jedem vorhergesagten Prüfungsergebnis und dem tatsächlichen Prüfungsergebnis berechnen. Wir können dann die Quadratwurzel aus dem Durchschnitt dieser Unterschiede ziehen:

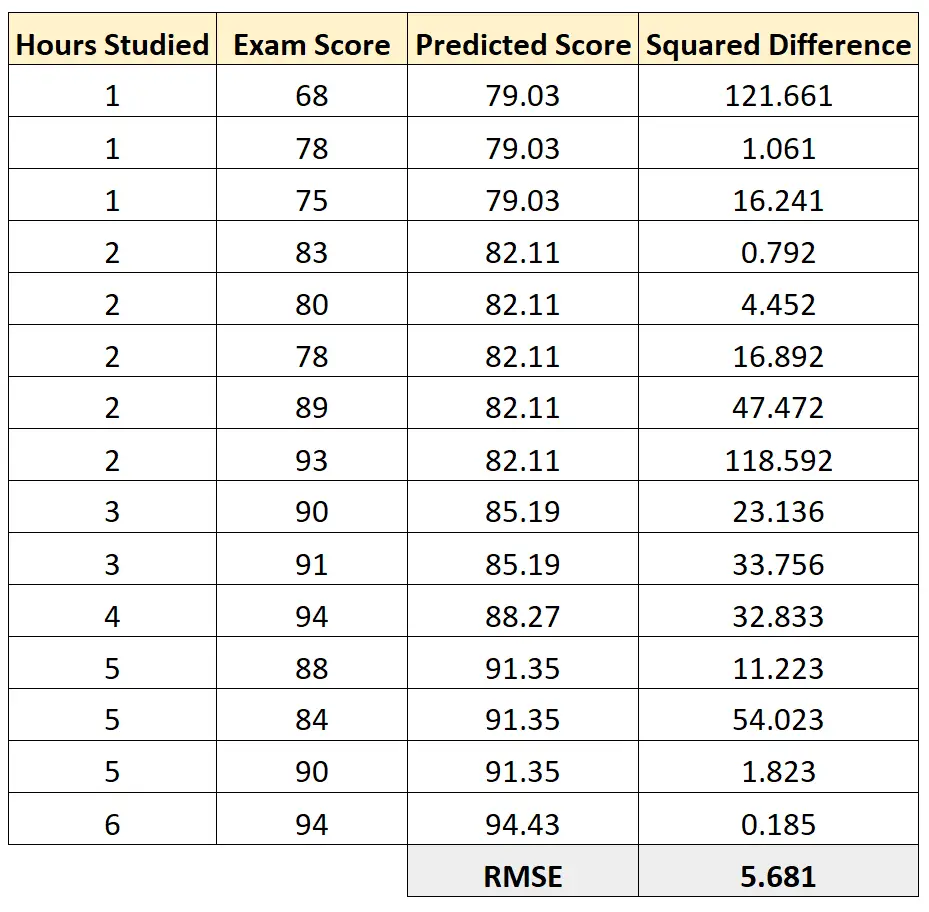
Der RMSE dieses Regressionsmodells beträgt 5,681 .

Denken Sie daran, dass die Residuen eines Regressionsmodells die Differenzen zwischen den beobachteten Datenwerten und den vorhergesagten Werten des Modells sind.

Residuum = (P _i – O _i )

Gold

• P _i ist der vorhergesagte Wert für die ^i-te Beobachtung im Datensatz
• O _i ist der beobachtete Wert für die ^i-te Beobachtung im Datensatz

Und denken Sie daran, dass der RMSE eines Regressionsmodells wie folgt berechnet wird:

RMSE = √ Σ(P _i – O _i ) ² / n

Das bedeutet, dass der RMSE die Quadratwurzel der Varianz der Residuen darstellt.

Dies ist ein nützlicher Wert, da er uns eine Vorstellung vom durchschnittlichen Abstand zwischen beobachteten Datenwerten und vorhergesagten Datenwerten gibt.

Dies steht im Gegensatz zum R-Quadrat des Modells, das uns sagt, wie viel der Varianz in der Antwortvariablen durch die Prädiktorvariablen des Modells erklärt werden kann.

Vergleich der RMSE-Werte verschiedener Modelle

Der RMSE ist besonders nützlich, um die Anpassung verschiedener Regressionsmodelle zu vergleichen.

Angenommen, wir möchten ein Regressionsmodell erstellen, um die Prüfungsergebnisse der Schüler vorherzusagen, und unter mehreren potenziellen Modellen das bestmögliche Modell finden.

Angenommen, wir passen drei verschiedene Regressionsmodelle an und ermitteln die entsprechenden RMSE-Werte:

• RMSE von Modell 1: 14,5
• RMSE von Modell 2: 16,7
• RMSE von Modell 3: 9,8

Modell 3 hat den niedrigsten RMSE, was uns sagt, dass es den Datensatz unter den drei potenziellen Modellen am besten anpassen kann.

Zusätzliche Ressourcen

RMSE-Rechner
So berechnen Sie den RMSE in Excel
So berechnen Sie RMSE in R
So berechnen Sie RMSE in Python