So führen sie eine anova mit wiederholten messungen in spss durch

Eine ANOVA mit wiederholten Messungen wird verwendet, um zu bestimmen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr Gruppen besteht, in denen in jeder Gruppe dieselben Probanden vorkommen.

In diesem Tutorial wird erläutert, wie Sie in SPSS eine einfaktorielle ANOVA mit wiederholten Messungen durchführen.

Beispiel: ANOVA mit wiederholten Messungen in SPSS

Die Forscher wollen wissen, ob vier verschiedene Medikamente unterschiedliche Reaktionszeiten verursachen. Um dies zu testen, maßen sie die Reaktionszeiten von fünf Patienten auf vier verschiedene Medikamente. Da bei jedem Patienten jedes der vier Medikamente gemessen wird, verwenden wir eine ANOVA mit wiederholten Messungen, um festzustellen, ob sich die mittlere Reaktionszeit zwischen den Medikamenten unterscheidet.

Führen Sie die folgenden Schritte aus, um eine ANOVA mit wiederholten Messungen in SPSS durchzuführen.

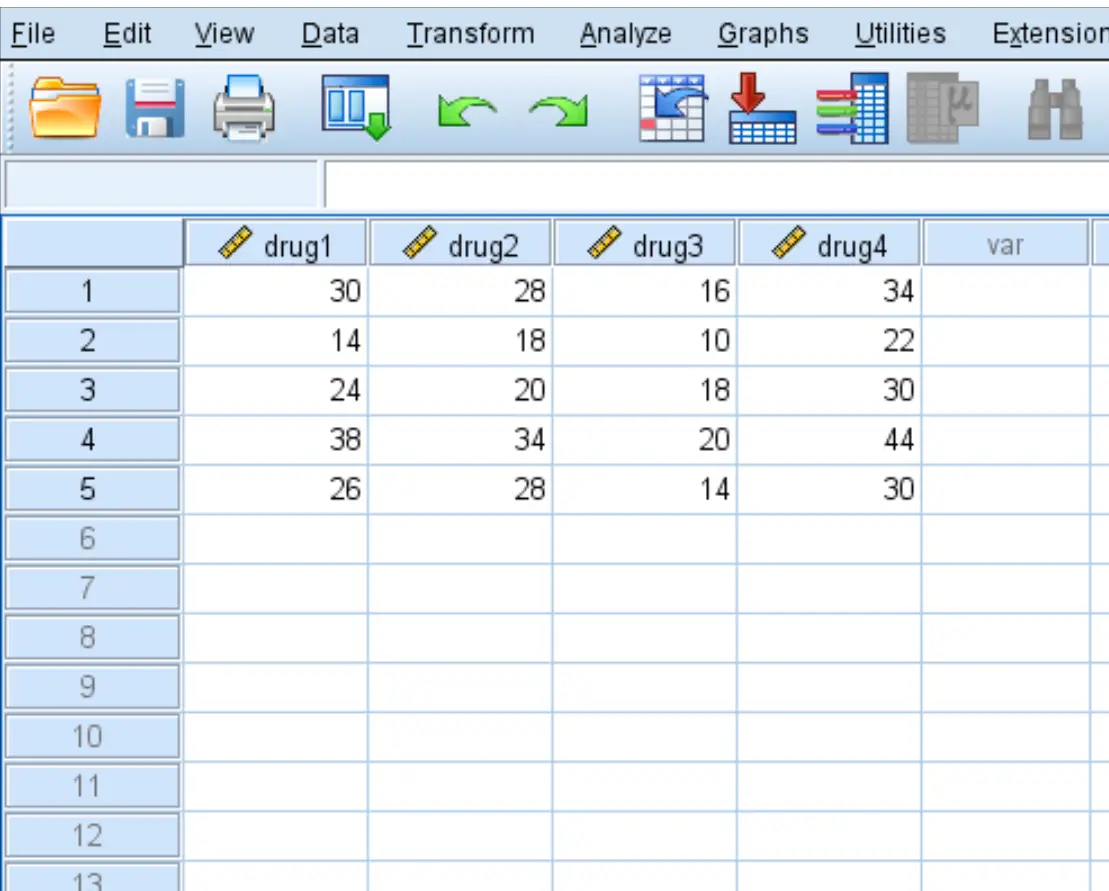
Schritt 1: Geben Sie die Daten ein.

Geben Sie die folgenden Daten ein, die die Reaktionszeit (in Sekunden) von fünf Patienten auf die vier Medikamente zeigen:

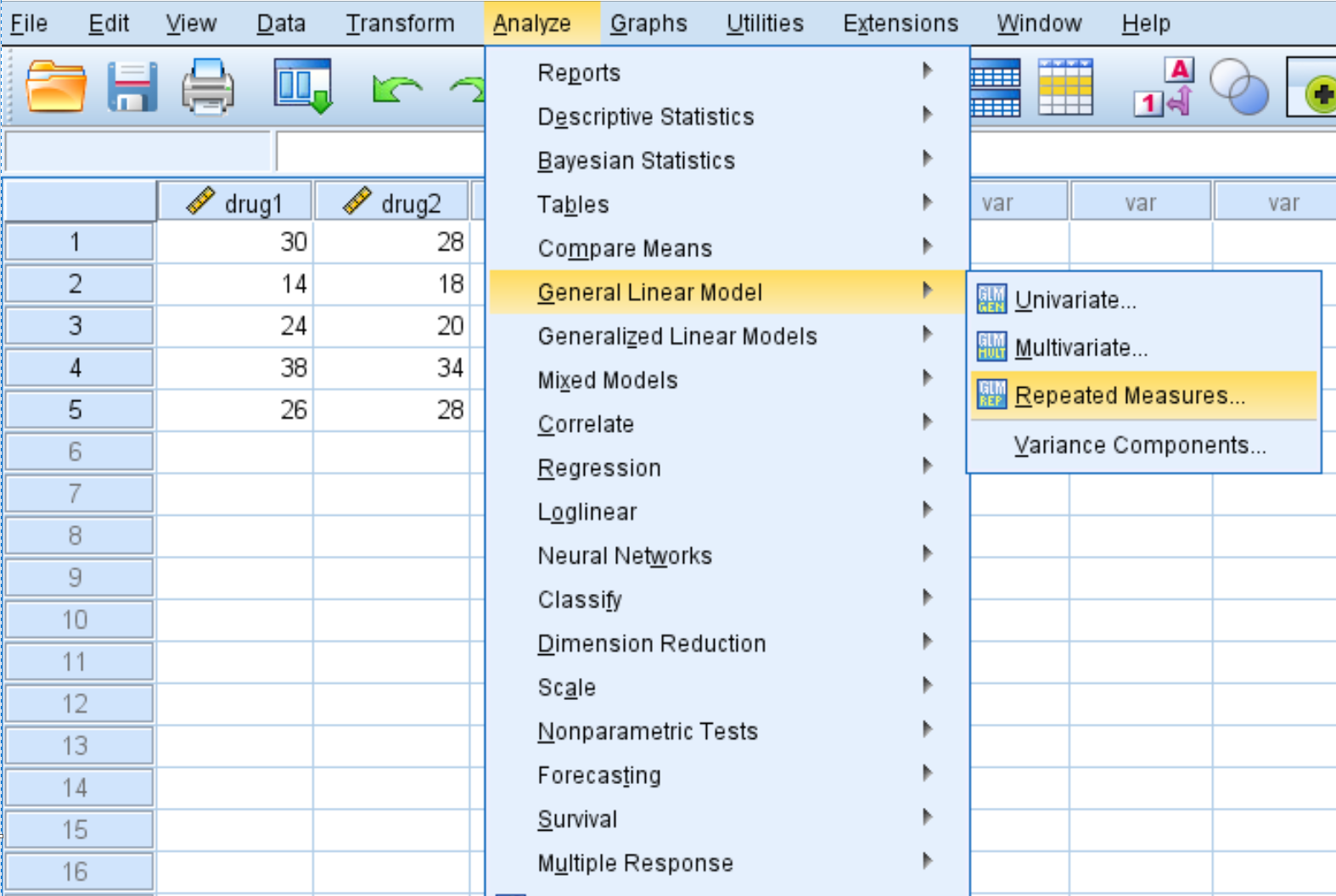
Schritt 2: Führen Sie eine ANOVA mit wiederholten Messungen durch.

Klicken Sie auf die Registerkarte „Analysieren“ , dann auf „Allgemeines lineares Modell“ und dann auf „Wiederholte Messungen“ :

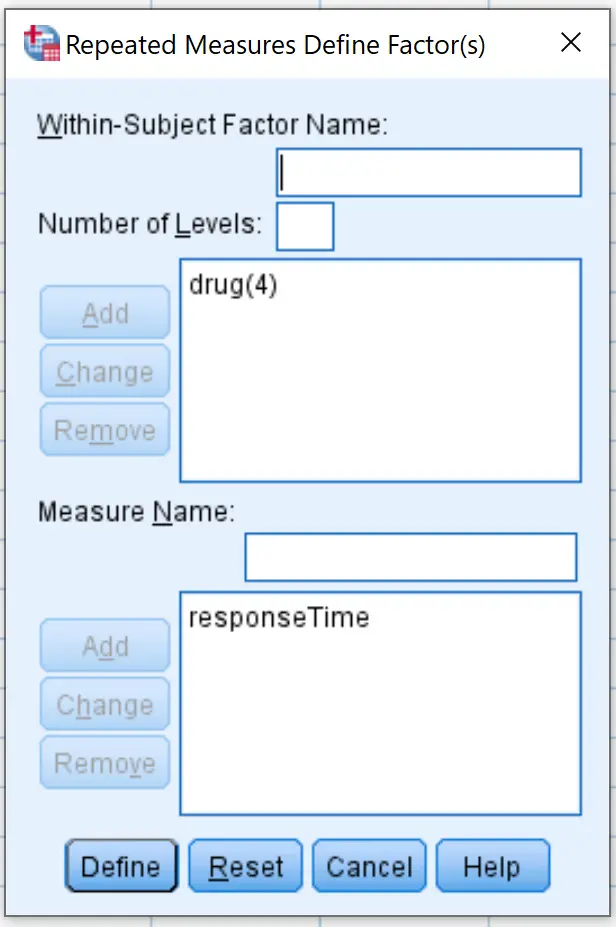
Geben Sie im neuen Fenster, das erscheint, das Medikament für den Namen des Intra-Subjekt-Faktors ein. Geben Sie 4 für die Anzahl der Stufen ein (da jeder Proband vier verschiedene Medikamente getestet hat) und klicken Sie dann auf „Hinzufügen“ . Geben Sie ResponseTime als Kennzahlname ein und klicken Sie dann auf Hinzufügen . Klicken Sie abschließend auf Festlegen .

Ziehen Sie im neuen Fenster, das erscheint, jede der vier Medikamentenvariablen in den Bereich mit der Bezeichnung „Innerhalb der Subjekte“-Variablen :

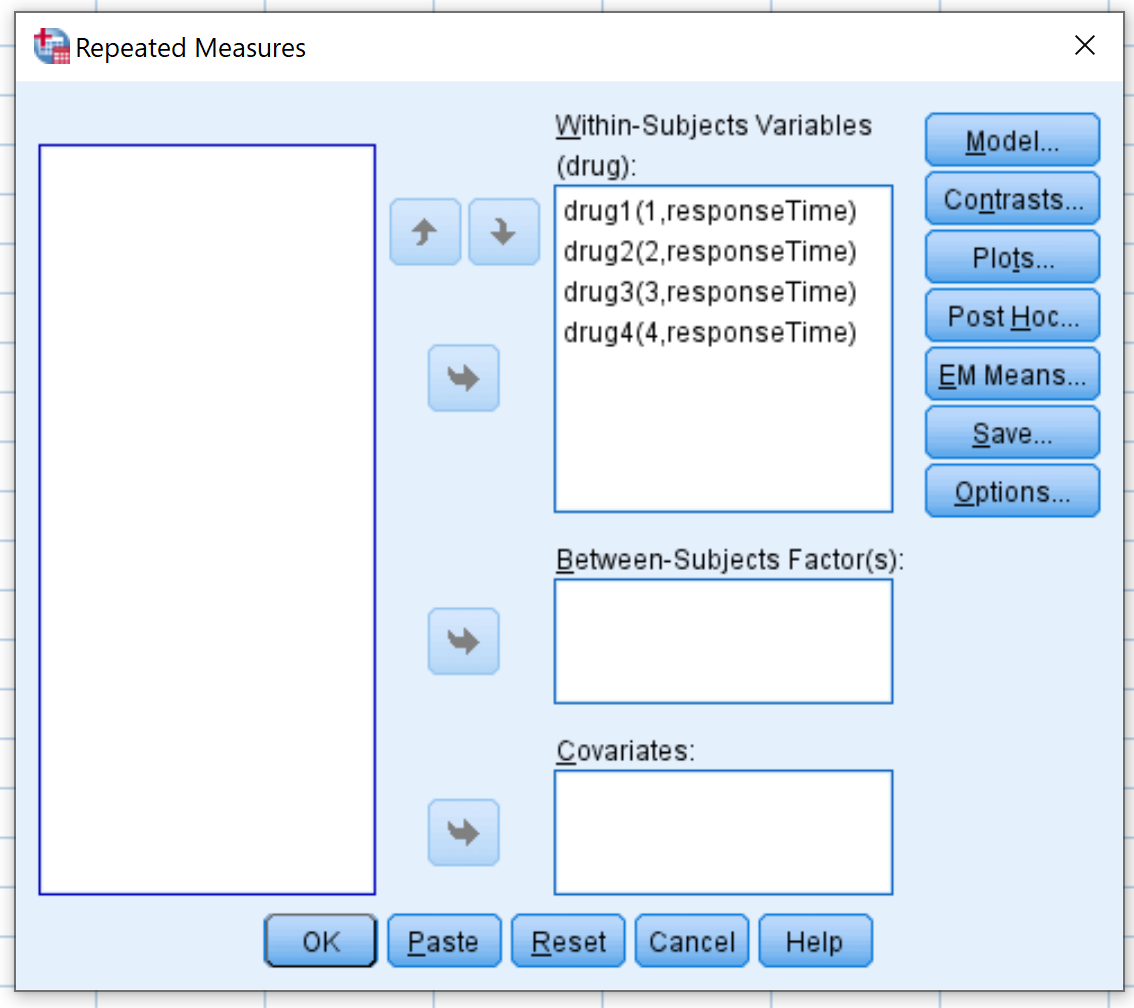
Klicken Sie anschließend auf Diagramme . Ziehen Sie das variable Medikament in den Bereich mit der Bezeichnung „Horizontale Achse“ . Klicken Sie dann auf Hinzufügen . Klicken Sie dann auf Weiter .

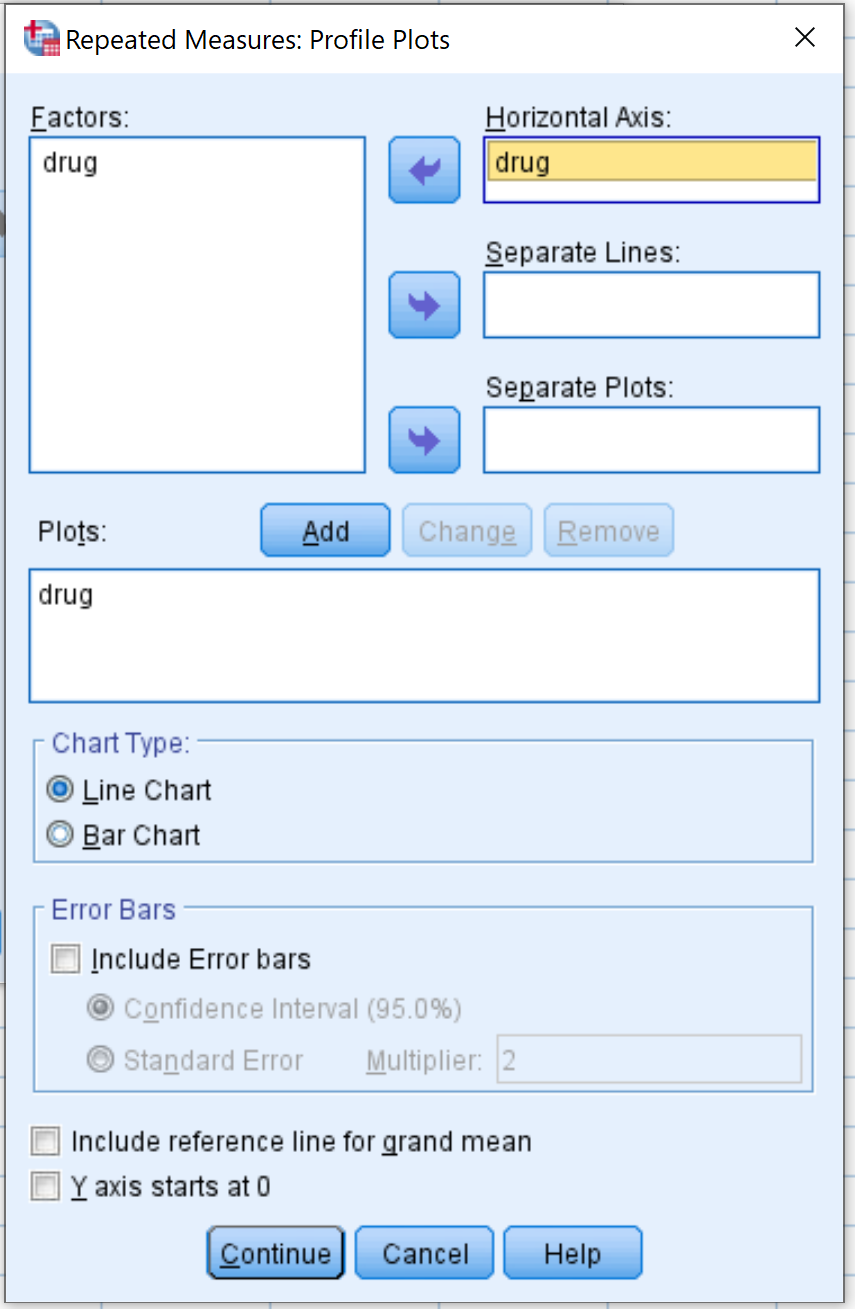
Klicken Sie anschließend auf EM-Mittel . Ziehen Sie die Arzneimittelvariable in das Feld mit der Bezeichnung „Mittelwerte anzeigen für“ . Aktivieren Sie dann das Kontrollkästchen neben „Haupteffekte vergleichen“ und wählen Sie „Bonferroni“ aus dem Dropdown-Menü aus. Klicken Sie dann auf Weiter .

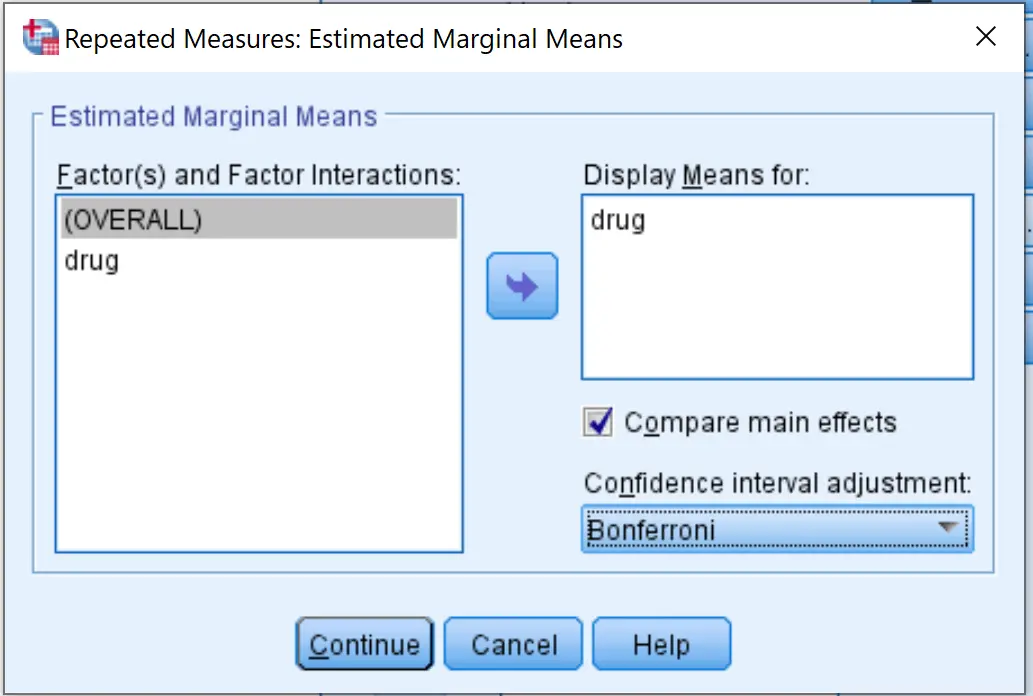
Klicken Sie abschließend auf OK .

Schritt 2: Interpretieren Sie die Ergebnisse.

Sobald Sie auf „OK“ klicken, werden die Ergebnisse der ANOVA mit wiederholten Messungen angezeigt. So interpretieren Sie das Ergebnis:

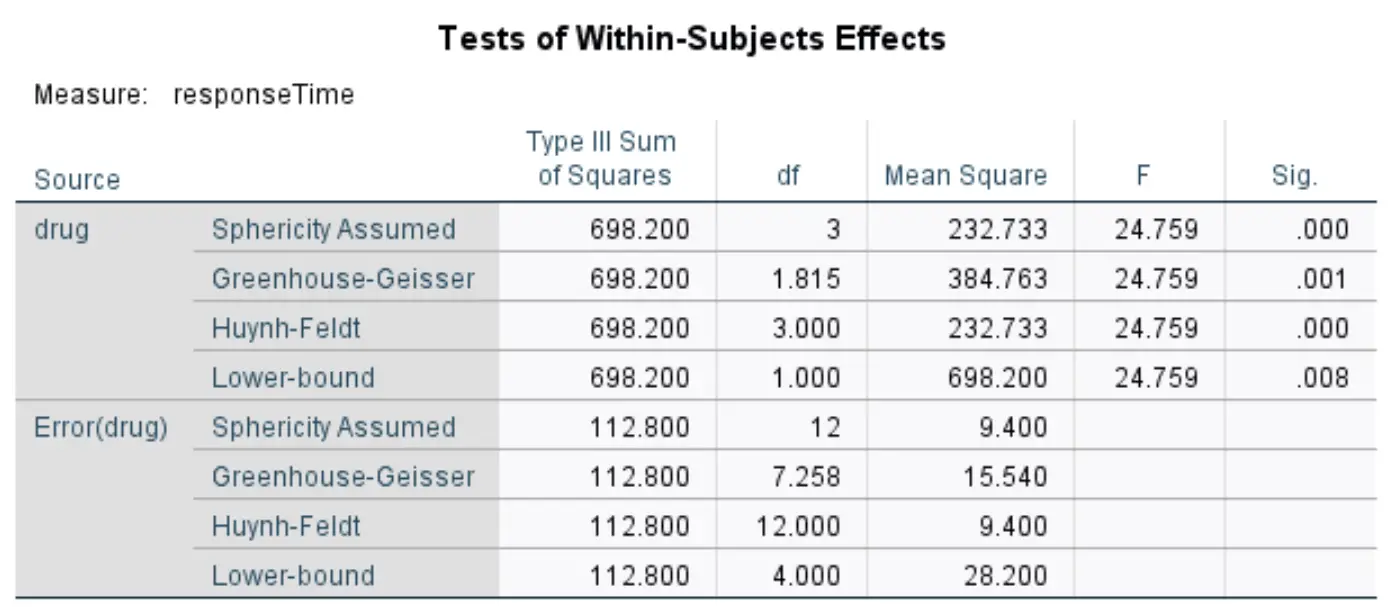
Tests innersubjektbezogener Effekte

Diese Tabelle zeigt die Gesamt-F-Statistik und den entsprechenden p-Wert der ANOVA mit wiederholten Messungen. Wir verwenden im Allgemeinen Werte aus der Linie mit der Bezeichnung Greenhouse-Geisser .

Gemäß dieser Zeile beträgt die F-Statistik 24,759 und der entsprechende p-Wert beträgt 0,001 . Da dieser p-Wert unter 0,05 liegt, können wir die Nullhypothese ablehnen und daraus schließen, dass es einen statistisch signifikanten Unterschied in den durchschnittlichen Reaktionszeiten zwischen den vier Medikamenten gibt.

Paarweise Vergleiche

Da wir die Nullhypothese abgelehnt haben, bedeutet dies, dass mindestens zwei Gruppenmittelwerte unterschiedlich sind. Um festzustellen, welche Mittelwertgruppen unterschiedlich sind, können wir diese Tabelle verwenden, die die paarweisen Vergleiche zwischen den einzelnen Arzneimitteln anzeigt.

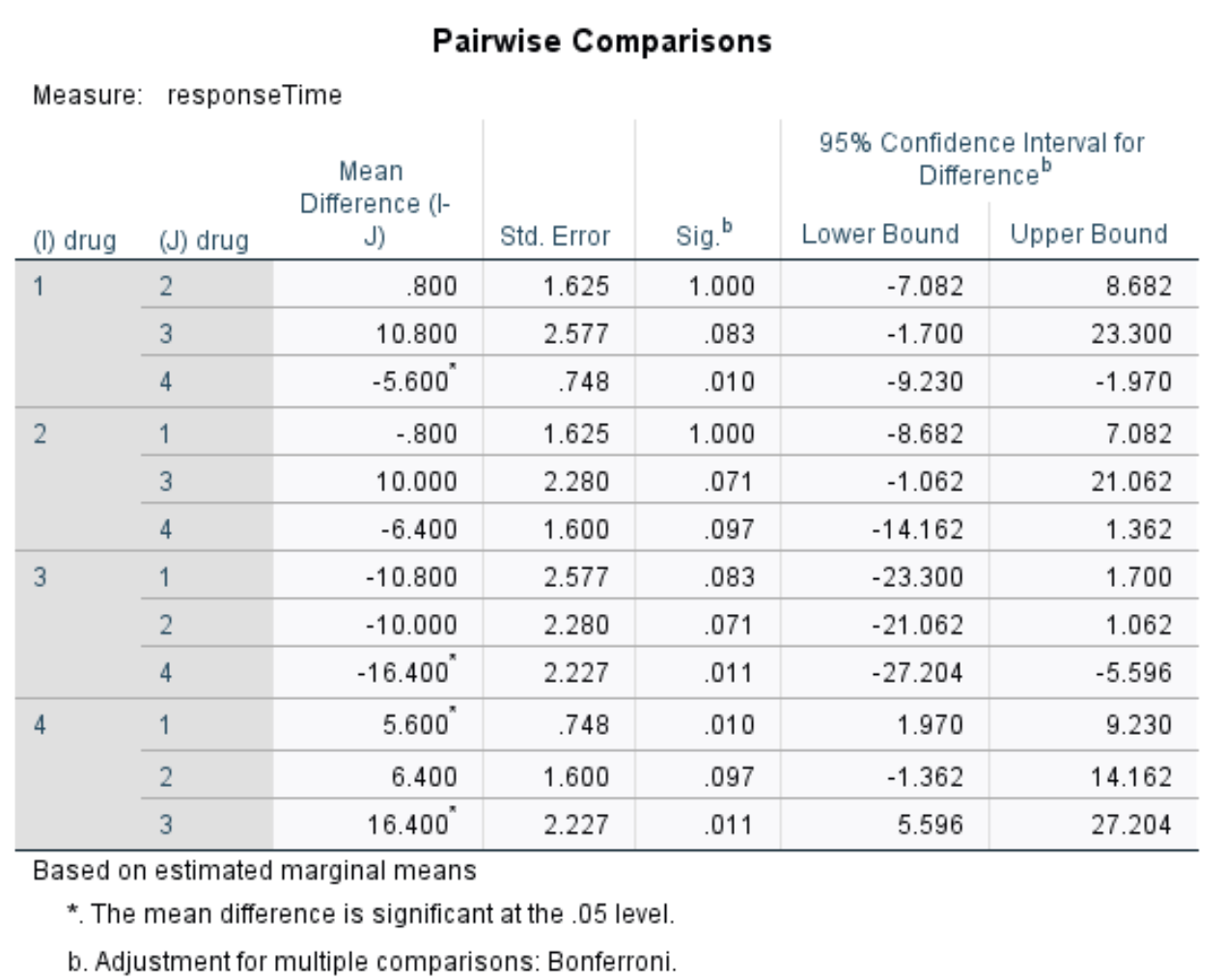
In der Tabelle sehen wir die p-Werte für die folgenden Vergleiche:

• Medikament 1 versus Medikament 2 | p-Wert = 1.000
• Medikament 1 versus Medikament 3 | p-Wert = 0,083
• Medikament 1 versus Medikament 4 | p-Wert = 0,010
• Medikament 2 versus Medikament 3 | p-Wert = 0,071
• Medikament 2 versus Medikament 4 | p-Wert = 0,097
• Medikament 3 versus Medikament 4 | p-Wert = 0,011

Die einzigen p-Werte unter 0,05 gelten für Arzneimittel 1 gegenüber Arzneimittel 4 und Arzneimittel 3 gegenüber Arzneimittel 4. Alle anderen Vergleiche weisen p-Werte über 0,05 auf.

Diagramm der geschätzten Grenzmittelwerte

Dieses Diagramm zeigt die geschätzten durchschnittlichen Reaktionszeiten für jedes Medikament. Aus der Grafik können wir deutlich erkennen, dass die Reaktionszeiten zwischen den vier verschiedenen Medikamenten erheblich variierten:

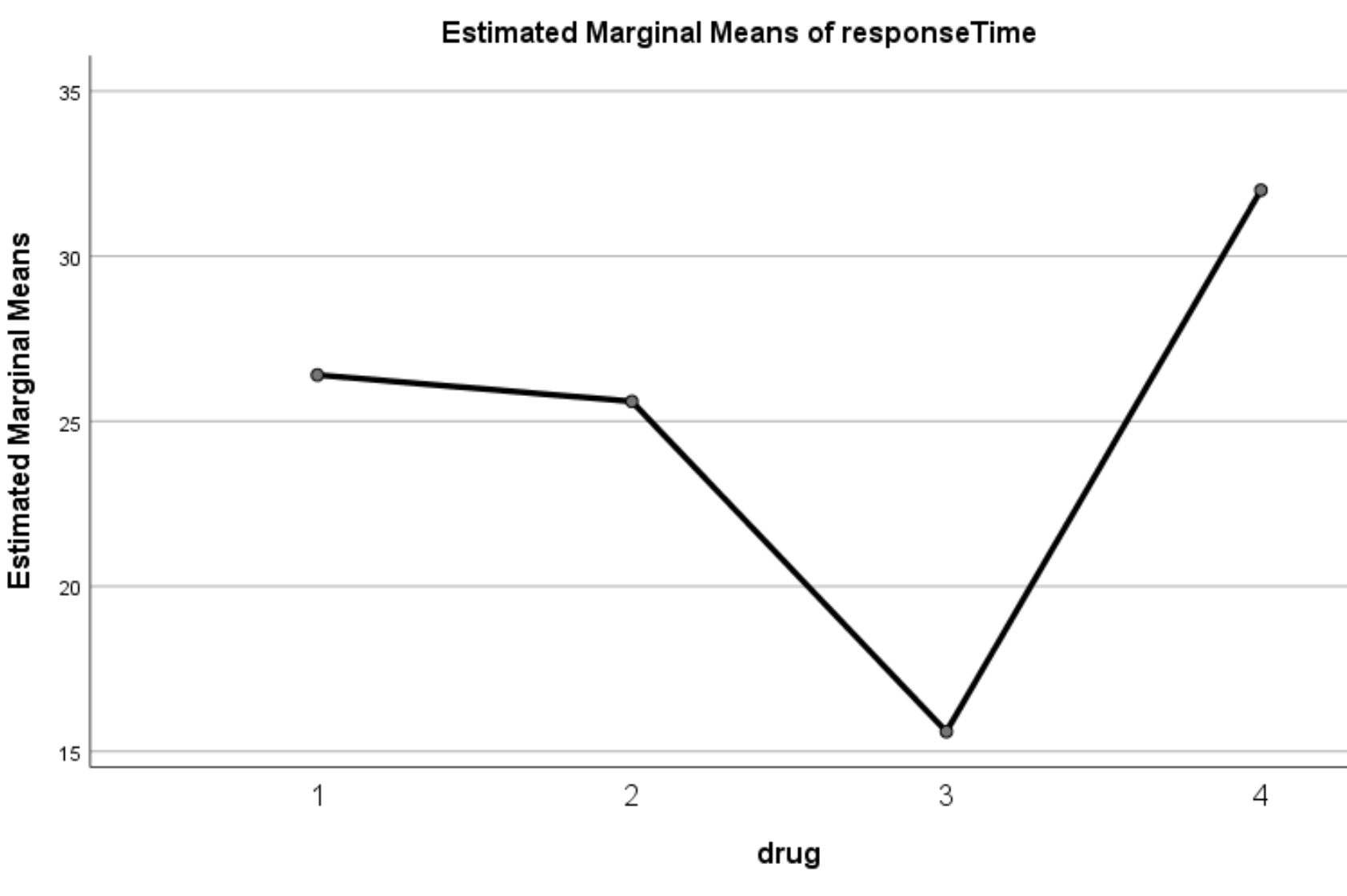
Schritt 3: Melden Sie die Ergebnisse.

Schließlich können wir die Ergebnisse der ANOVA mit wiederholten Messungen berichten. Hier ist ein Beispiel dafür:

Eine einfaktorielle ANOVA mit wiederholten Messungen wurde durchgeführt, um zu bestimmen, ob sich die mittlere Reaktionszeit der Patienten zwischen vier verschiedenen Medikamenten unterschied.

Eine einfaktorielle ANOVA mit wiederholten Messungen ergab, dass die Art der verwendeten Medikamente zu statistisch signifikanten Unterschieden in der Reaktionszeit führte (F = 24,75887, p = 0,001).

Der Bonferroni-Test für mehrere Vergleiche ergab, dass es einen statistisch signifikanten Unterschied in den Reaktionszeiten zwischen Patienten gab, die Medikament 1 und Medikament 4 sowie Medikament 3 und Medikament 4 einnahmen.