So führen sie den wilcoxon signed rank test durch
Der vorzeichenbehaftete Wilcoxon-Rangtest ist die nichtparametrische Version des gepaarten t-Tests . Es wird verwendet, um zu testen, ob zwischen zwei Populationsmittelwerten ein signifikanter Unterschied besteht.
Wann ist der von Wilcoxon signierte Rangtest zu verwenden?
Verwenden Sie den Wilcoxon-Signed-Rang-Test, wenn Sie den gepaarten t-Test verwenden möchten, die Verteilung der Unterschiede zwischen Paaren jedoch stark von der Normalverteilung abweicht .
Der einfachste Weg, festzustellen, ob die Unterschiede nicht normalverteilt sind, besteht darin, ein Histogramm der Unterschiede zu erstellen und zu prüfen, ob sie einer einigermaßen normalen, „glockenförmigen“ Verteilung folgen.
Beachten Sie, dass der gepaarte t-Test recht robust gegenüber Abweichungen von der Normalverteilung ist. Daher muss die Abweichung von einer Normalverteilung groß genug sein, um die Verwendung des Wilcoxon-Signed-Rank-Tests zu rechtfertigen.
So machen Sie den Wilcoxon Signed Rank Test
Das folgende Beispiel veranschaulicht, wie der Wilcoxon Signed Rank-Test durchgeführt wird.
Ein Basketballtrainer möchte wissen, ob ein bestimmtes Trainingsprogramm die Anzahl der Freiwürfe seiner Spieler erhöht. Um dies zu testen, forderte er 15 Spieler auf, vor und nach dem Trainingsprogramm jeweils 20 Freiwürfe auszuführen.
Da jeder Spieler mit sich selbst „gepaart“ werden kann, plante der Trainer die Verwendung eines gepaarten T-Tests, um festzustellen, ob es einen signifikanten Unterschied zwischen der durchschnittlichen Anzahl der Freiwürfe vor und nach dem Trainingsprogramm gab. Ausbildung.
Allerdings erweist sich die Verteilung der Unterschiede als nicht normal, weshalb der Trainer stattdessen einen von Wilcoxon signierten Rangtest verwendet.
Die folgende Tabelle zeigt die Anzahl der von jedem der 15 Spieler vor und nach dem Trainingsprogramm ausgeführten Freiwürfe (von 20 Versuchen):
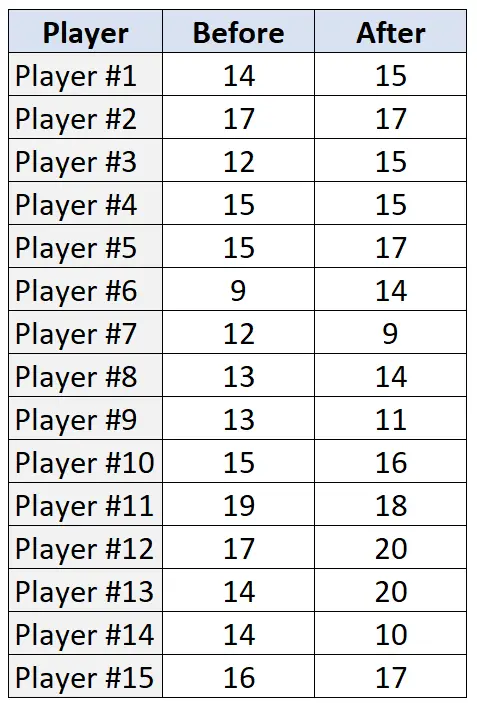
Schritt 1: Geben Sie die Null- und Alternativhypothese an.
H 0 : Der mittlere Unterschied zwischen den beiden Gruppen ist Null.
H A : Die mittlere Differenz ist negativ. (z. B. machen Spieler weniger Freiwürfe, bevor sie am Trainingsprogramm teilnehmen)
Schritt 2: Ermitteln Sie die Differenz und die absolute Differenz für jedes Paar.
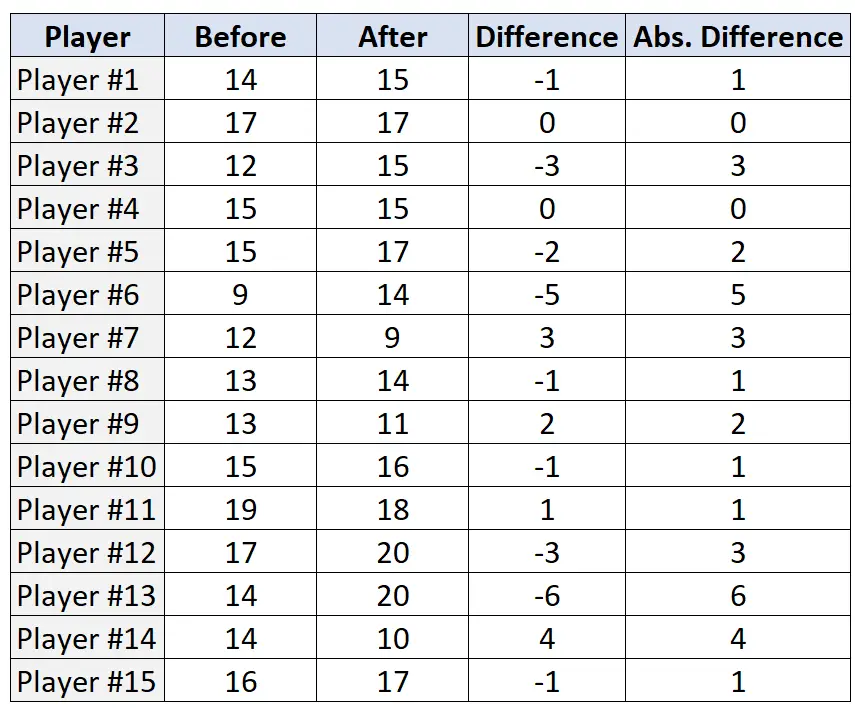
Schritt 3: Ordnen Sie die Paare basierend auf absoluten Unterschieden und weisen Sie eine Rangfolge vom kleinsten zum größten absoluten Unterschied zu. Ignorieren Sie Paare mit einer absoluten Differenz von „0“ und weisen Sie im Falle eines Unentschiedens Durchschnittsränge zu.
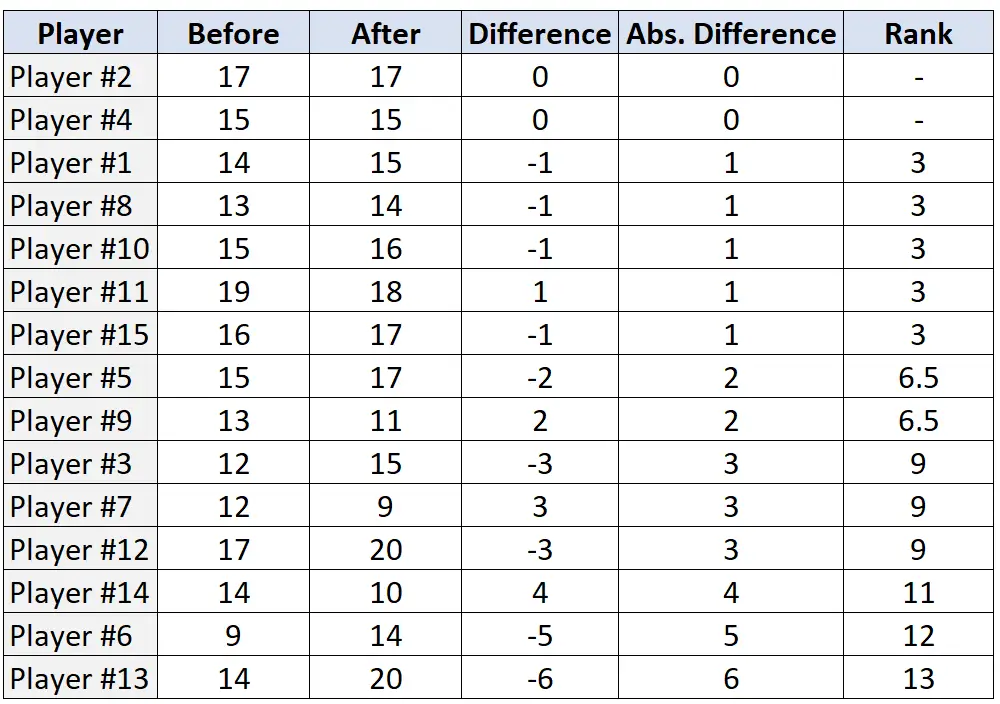
Schritt 4: Ermitteln Sie die Summe der positiven und negativen Ränge.
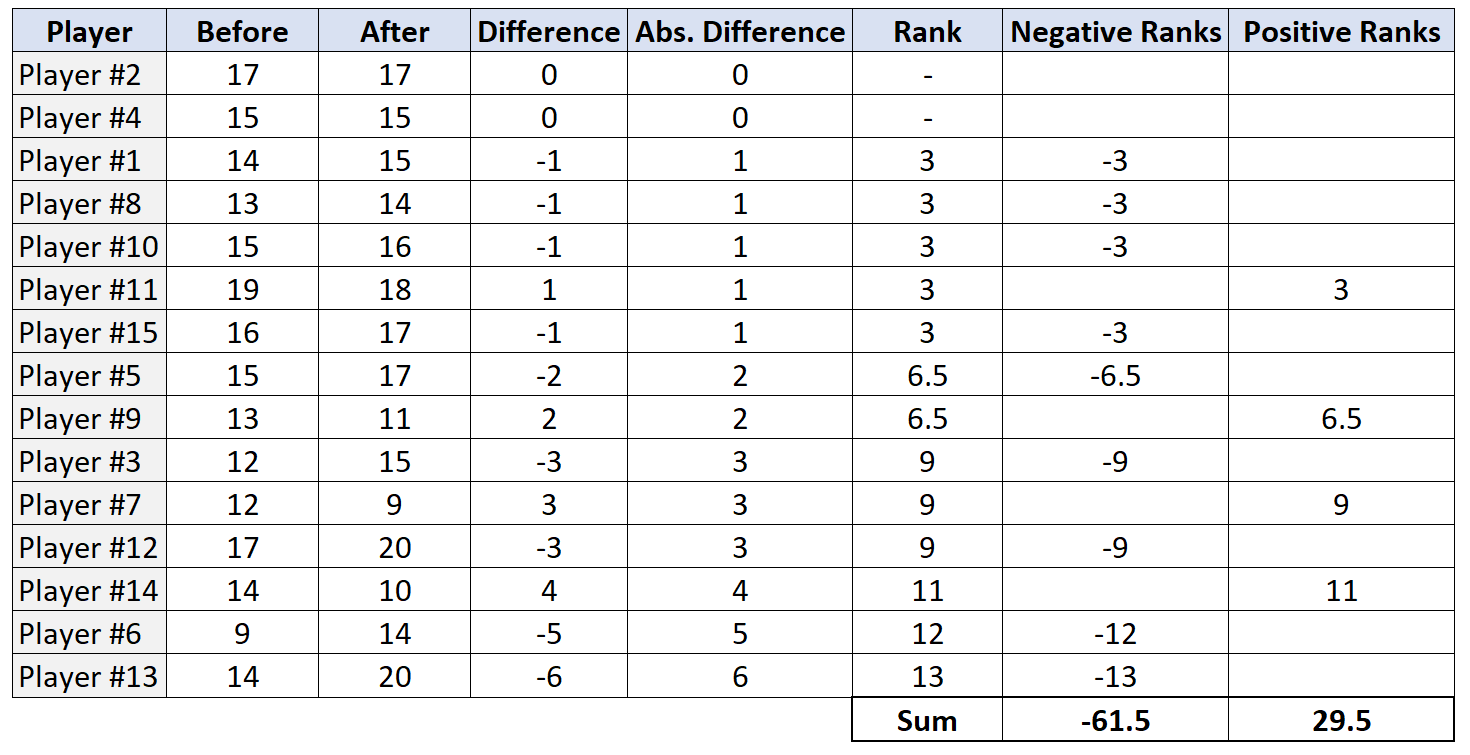
Schritt 5: Lehnen Sie die Nullhypothese ab oder lehnen Sie sie nicht ab.
Die Teststatistik W ist der kleinste der absoluten Werte der positiven Ränge und der negativen Ränge. In diesem Fall beträgt der kleinste Wert 29,5. Unsere Teststatistik lautet also W = 29,5 .
Um zu bestimmen, ob wir die Nullhypothese ablehnen sollten oder nicht, können wir uns auf den kritischen Wert beziehen, der in der Tabelle mit den kritischen Werten des vorzeichenbehafteten Rangtests von Wilcoxon gefunden wird und n und dem gewählten Alpha-Level entspricht.
Wenn unsere Teststatistik W kleiner oder gleich dem kritischen Wert in der Tabelle ist, können wir die Nullhypothese ablehnen. Andernfalls können wir die Nullhypothese nicht ablehnen.
Der kritische Wert, der einem Alpha-Level von 0,05 und n = 13 entspricht (die Gesamtzahl der Paare abzüglich der beiden, für die wir keinen Rang berechnet haben, weil sie eine beobachtete Differenz von 0 hatten), ist 17 .
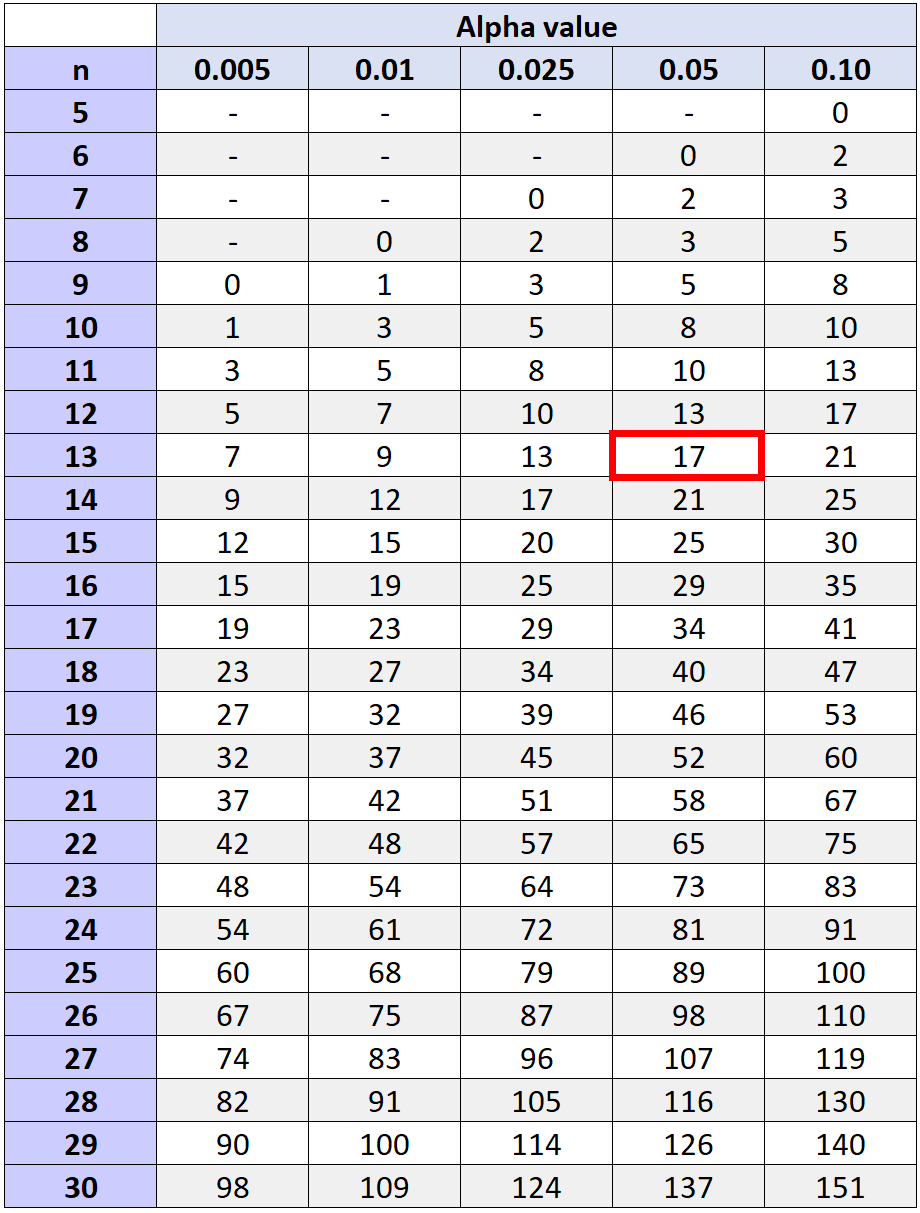
Da unsere Teststatistik (W = 29,5) nicht kleiner oder gleich 17 ist, können wir die Nullhypothese nicht ablehnen. Wir haben keine ausreichenden Beweise dafür, dass das Trainingsprogramm zu einer signifikanten Steigerung der Anzahl der von den Spielern ausgeführten Freiwürfe führt.
Hinweis: Verwenden Sie den Wilcoxon Signed Rank Test Calculator , wenn Sie den Test mit einem Taschenrechner statt von Hand durchführen möchten.