So führen sie den wilcoxon-signed-rang-test in r durch

Der Wilcoxon-Signed-Rank-Test ist die nichtparametrische Version des gepaarten t-Tests . Es wird verwendet, um zu testen, ob ein signifikanter Unterschied zwischen den Mittelwerten zweier Grundgesamtheiten besteht, wenn die Verteilung der Unterschiede zwischen den beiden Stichproben nicht als normal angesehen werden kann.

In diesem Tutorial wird erklärt, wie man einen Wilcoxon-Signed-Rank-Test in R durchführt.

Beispiel: Wilcoxon unterzeichnete einen Rangtest in R

Angenommen, ein Basketballtrainer möchte wissen, ob ein bestimmtes Trainingsprogramm die Anzahl der Freiwürfe seiner Spieler erhöht. Um dies zu testen, forderte er 15 Spieler auf, vor und nach dem Trainingsprogramm jeweils 20 Freiwürfe auszuführen.

Da jeder Spieler mit sich selbst „gepaart“ werden kann, plante der Trainer die Verwendung eines gepaarten T-Tests, um festzustellen, ob es einen signifikanten Unterschied zwischen der durchschnittlichen Anzahl der Freiwürfe vor und nach dem Trainingsprogramm gab. Ausbildung. Allerdings erweist sich die Verteilung der Unterschiede als nicht normal, weshalb der Trainer stattdessen einen Wilcoxon-Signed-Rank-Test verwendet.

Die folgende Tabelle zeigt die Anzahl der von jedem der 15 Spieler vor und nach dem Trainingsprogramm ausgeführten Freiwürfe (von 20 Versuchen):

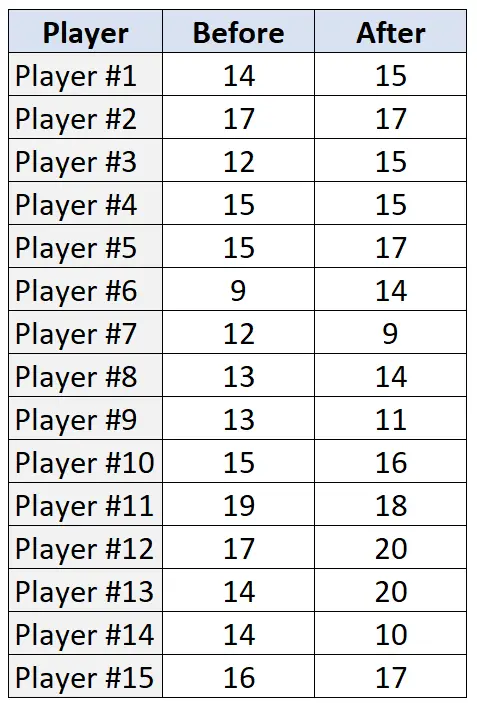
Um den Wilcoxon-Signed-Rank-Test für diese Daten in R durchzuführen, können wir die Funktion wilcox.test() verwenden, die die folgende Syntax verwendet:

wilcox.test(x, y, gerade = WAHR)

Gold:

• x, y: zwei Vektoren von Datenwerten
• gepaart: Wenn Sie dies auf TRUE setzen, wird R mitgeteilt, dass unsere beiden Vektoren gepaarte Daten enthielten

Der folgende Code zeigt, wie diese Funktion verwendet wird, um den Wilcoxon Signed-Rank-Test für diese Daten durchzuführen:

 #create the two vectors of data
before <- c(14, 17, 12, 15, 15, 9, 12, 13, 13, 15, 19, 17, 14, 14, 16)
after <- c(15, 17, 15, 15, 17, 14, 9, 14, 11, 16, 18, 20, 20, 10, 17)

#perform Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE)

	Wilcoxon signed rank test with continuity correction

data: before and after
V = 29.5, p-value = 0.275
alternative hypothesis: true location shift is not equal to 0

Die Teststatistik beträgt 29,5 und der entsprechende p-Wert beträgt 0,275 . Da dieser p-Wert nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen. Es gab keinen statistisch signifikanten Unterschied in der Anzahl der Freiwürfe vor und nach der Teilnahme der Spieler am Trainingsprogramm.

Standardmäßig führt diese Funktion einen zweiseitigen Wilcoxon-Signed-Rank-Test durch, Sie können jedoch mit dem alternativen Argument einen linkshändigen oder einen rechtshändigen Test angeben:

 #perform left-tailed Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE, alternative="less")

	Wilcoxon signed rank test with continuity correction

data: before and after
V = 29.5, p-value = 0.1375
alternative hypothesis: true location shift is less than 0

#perform right-tailed Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE, alternative="greater")

	Wilcoxon signed rank test with continuity correction

data: before and after
V = 29.5, p-value = 0.8774
alternative hypothesis: true location shift is greater than 0

Zusätzliche Ressourcen

Eine Einführung in den Wilcoxon Signed Rank Test
Von Wilcoxon signierter Ortstest-Rechner