Yate-kontinuitätskorrektur: definition und beispiel
EinChi-Quadrat-Unabhängigkeitstest wird verwendet, um zu bestimmen, ob zwischen zwei kategorialen Variablen ein signifikanter Zusammenhang besteht oder nicht.
Dieser Test verwendet die folgenden Null- und Alternativhypothesen:
- H 0 : (Nullhypothese) Die beiden Variablen sind unabhängig.
- H 1 : (Alternativhypothese) Die beiden Variablen sind nicht unabhängig. (d. h. sie sind verbunden)
Wir verwenden die folgende Formel, um die Chi-Quadrat-x- 2 -Teststatistik für diesen Test zu berechnen:
X 2 = Σ(O i -E i ) 2 / E i
Gold:
- Σ: ist ein ausgefallenes Symbol, das „Summe“ bedeutet
- O: beobachteter Wert
- E: erwarteter Wert
Bei diesem Test wird davon ausgegangen, dass die diskreten Wahrscheinlichkeiten von Häufigkeiten in einer Kontingenztabelle durch die Chi-Quadrat-Verteilung angenähert werden können, bei der es sich um eine kontinuierliche Verteilung handelt.
Diese Annahme ist jedoch tendenziell etwas falsch und die resultierenden Teststatistiken sind tendenziell nach oben verzerrt.
Um diese Verzerrung zu korrigieren, können wir die Kontinuitätskorrektur von Yate anwenden, die die folgende Korrektur auf die Formel X2 anwendet:
X 2 = Σ(|O i -E i | – 0,5) 2 / E i
Wir verwenden diese Korrektur im Allgemeinen nur, wenn mindestens eine Zelle in der Kontingenztabelle eine erwartete Häufigkeit von weniger als 5 aufweist.
Beispiel: Anwendung der Kontinuitätskorrektur von Yate
Angenommen, wir möchten wissen, ob das Geschlecht mit der Präferenz für eine politische Partei zusammenhängt oder nicht. Wir nehmen eine einfache Zufallsstichprobe von 40 Wählern und befragen sie zu ihrer politischen Parteipräferenz. Die folgende Tabelle stellt die Ergebnisse der Umfrage dar:

So führen Sie einen Chi-Quadrat-Test der Unabhängigkeit mit der Kontinuitätskorrektur von Yate durch:
Beobachtete Werte:

Erwartete Werte:
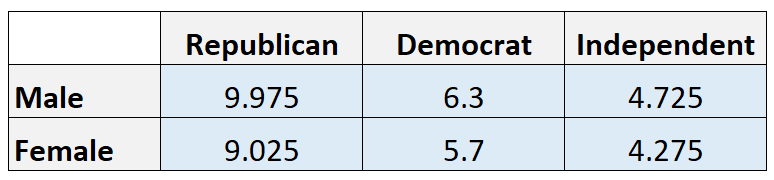
Hinweis: Wir berechnen den erwarteten Wert in jeder Zelle, indem wir die Zeilensumme mit der Spaltensumme multiplizieren und dann durch die Gesamtsumme dividieren. Beispielsweise beträgt die erwartete Anzahl republikanischer Männer (21*19)/40 = 9,975.
Chi – Quadrat – Teststatistik :
- (|8-9,975| – 0,5) 2 / 9,975 = 0,218
- (|9-6,3| – 0,5) 2 / 6,3 = 0,768
- (|4-4,725| – 0,5) 2 / 4,725 = 0,011
- (|11-9,025| – 0,5) 2 / 9,025 = 0,241
- (|3-5,7| – 0,5) 2 / 5,7 = 0,849
- (|5-4,275| – 0,5) 2 / 4,275 = 0,012
Also ,
P-Wert: Laut dem Chi-Quadrat-zu-P-Wert-Rechner beträgt der p-Wert, der einer Chi-Quadrat-Teststatistik mit 2 Freiheitsgraden entspricht, 0,3501 .
Da dieser p-Wert nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen. Das bedeutet, dass uns keine ausreichenden Belege dafür vorliegen, dass ein Zusammenhang zwischen Geschlecht und politischen Parteipräferenzen besteht.