So berechnen sie z-scores in spss

Ein Z-Score sagt uns, wie viele Standardabweichungen ein bestimmter Wert vom Mittelwert hat.

Der Z-Score eines bestimmten Werts wird wie folgt berechnet:

Z-Score = (x – μ) / σ

Gold:

• x: individueller Wert
• μ: Bevölkerungsdurchschnitt
• σ: Populationsstandardabweichung

In diesem Tutorial wird erläutert, wie Z-Scores in SPSS berechnet werden.

Verwandte Themen: So interpretieren Sie Z-Scores

So berechnen Sie Z-Scores in SPSS

Angenommen, wir haben den folgenden Datensatz, der das Jahreseinkommen (in Tausend) von 15 Personen zeigt:

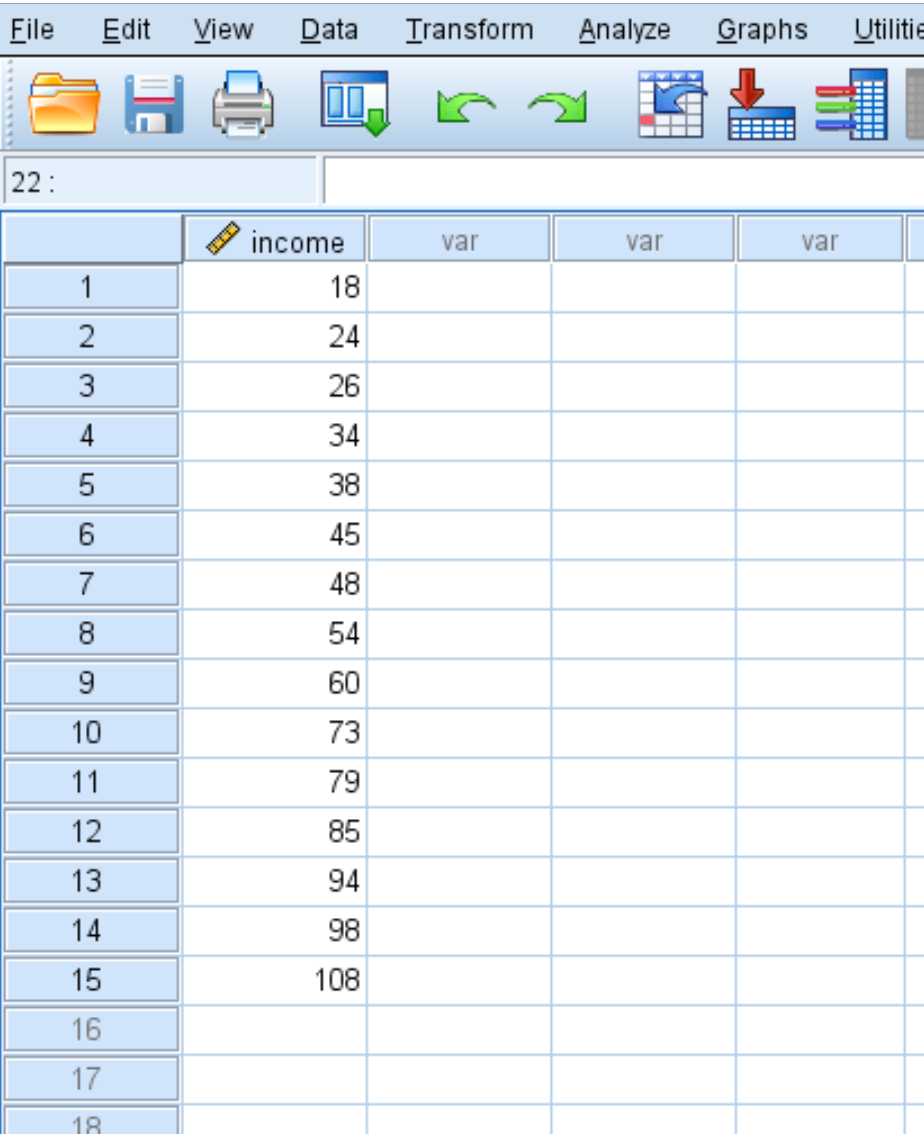
Um Z-Scores für jeden Wert im Datensatz zu berechnen, klicken Sie auf die Registerkarte „Analysieren “, dann auf „Beschreibende Statistik“ und dann auf „Beschreibend“ :

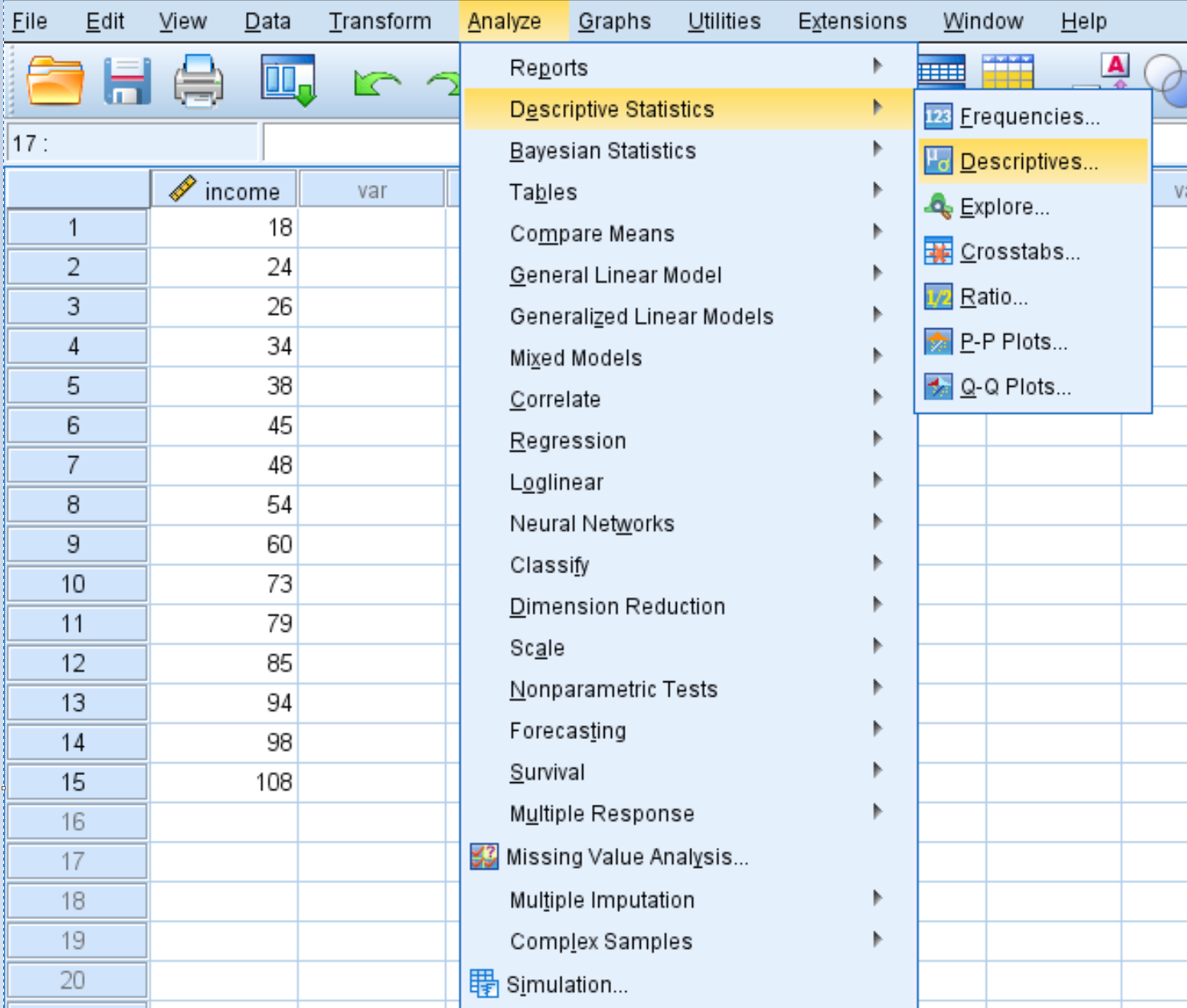
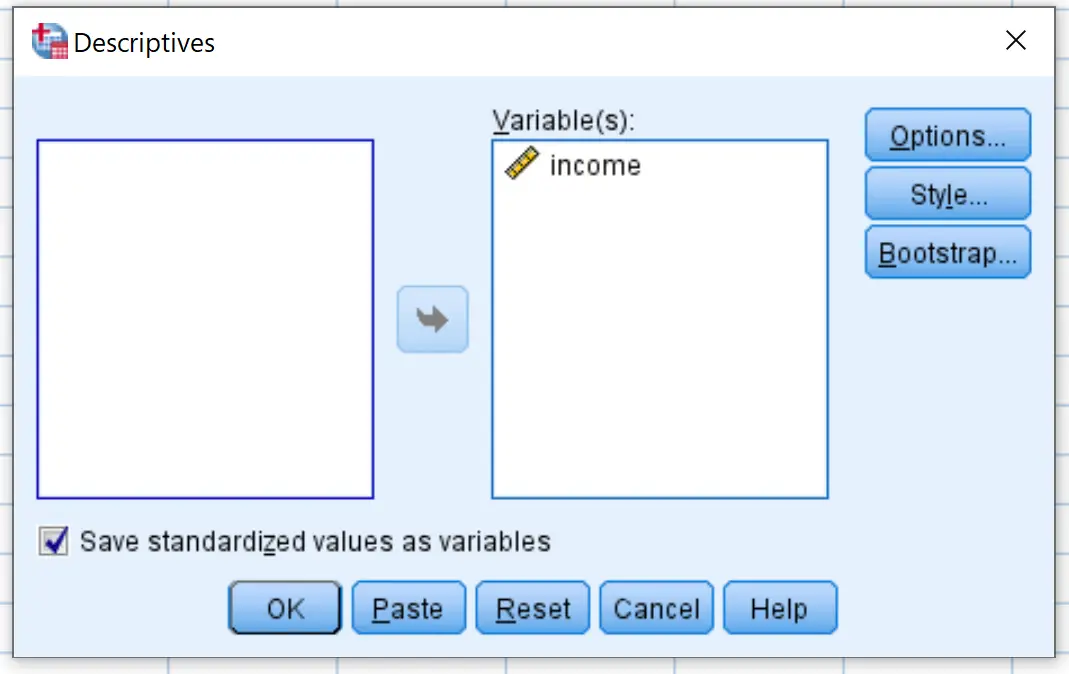
Ziehen Sie im neuen Fenster, das erscheint, die Einkommensvariable in das Feld mit der Bezeichnung „Variable(n)“.

Stellen Sie sicher, dass das Kontrollkästchen neben Standardisierte Werte als Variablen speichern aktiviert ist, und klicken Sie dann auf OK .

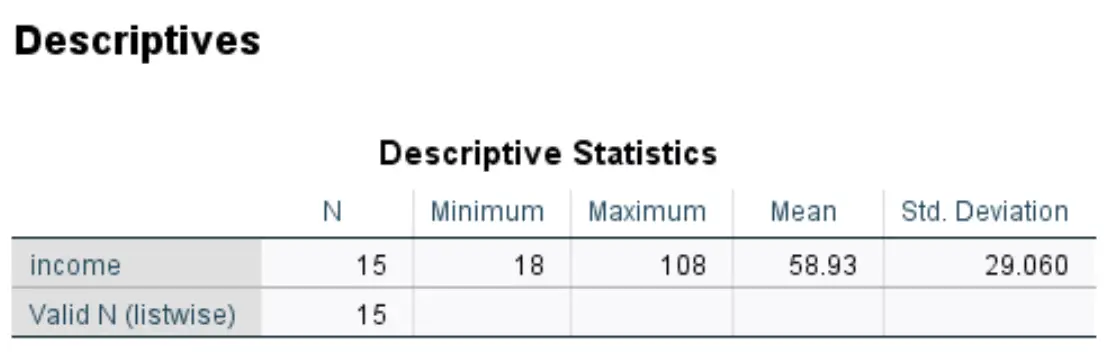
Sobald Sie auf „OK“ klicken, erstellt SPSS eine Tabelle mit beschreibenden Statistiken für Ihren Datensatz:

SPSS erstellt außerdem eine neue Wertespalte, die den Z-Score für jeden der ursprünglichen Werte in Ihrem Datensatz anzeigt:

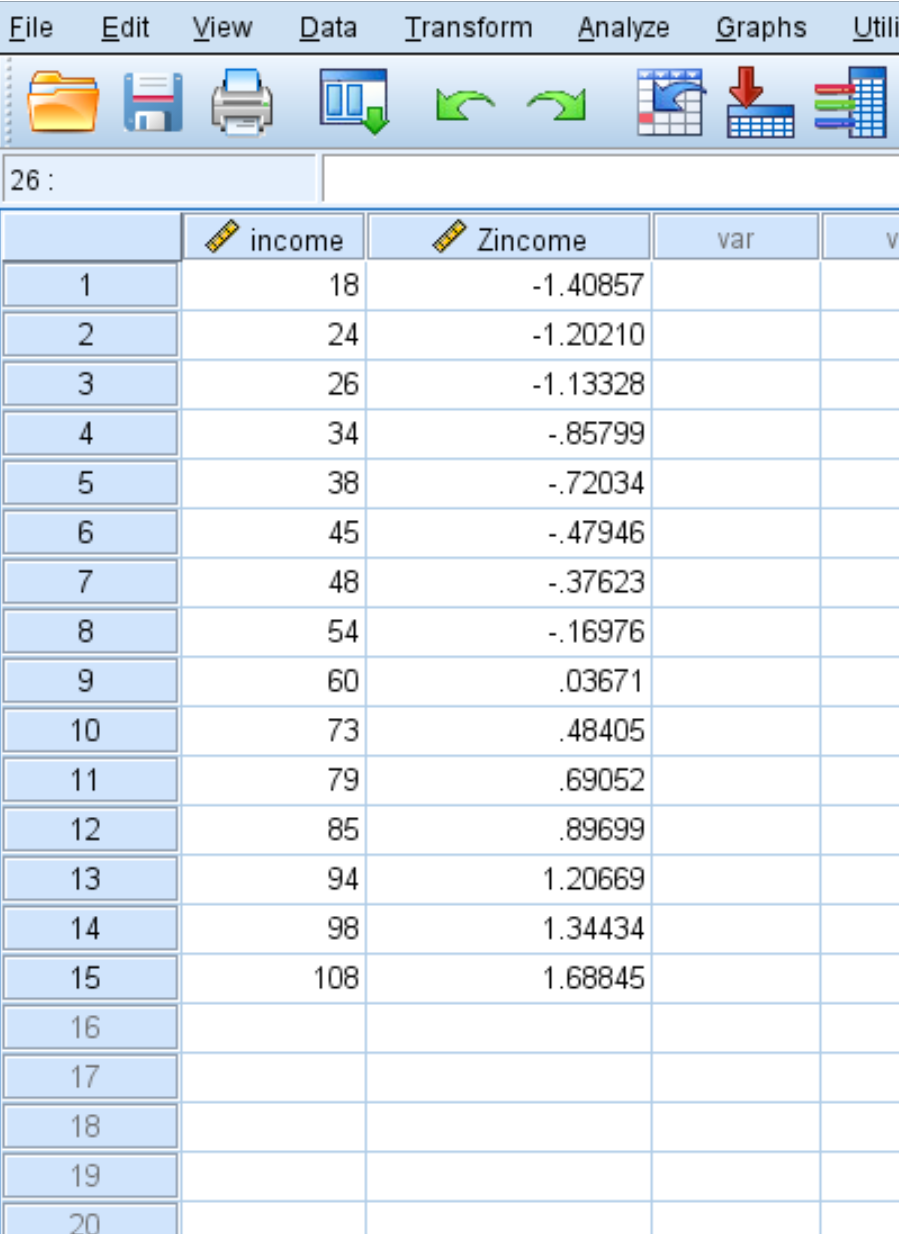
Jeder der z-Scores wird anhand der Formel z = (x – μ) / σ berechnet

Der Z-Score für den Einkommenswert 18 lautet beispielsweise:

z = (18 – 58,93) / 29,060 = -1,40857 .

Z-Scores für alle anderen Datenwerte werden auf die gleiche Weise berechnet.

So interpretieren Sie Z-Scores

Denken Sie daran, dass ein Z-Score uns einfach sagt, wie viele Standardabweichungen ein Wert vom Mittelwert hat.

Ein Z-Score kann positiv, negativ oder gleich Null sein:

• Ein positiver Z-Score zeigt an, dass ein bestimmter Wert über dem Durchschnitt liegt.
• Ein negativer Z-Score zeigt an, dass ein bestimmter Wert unter dem Durchschnitt liegt.
• Ein Z-Score von Null zeigt an, dass ein bestimmter Wert dem Mittelwert entspricht.

In unserem Beispiel haben wir festgestellt, dass der Mittelwert 58,93 und die Standardabweichung 29,060 betrug.

Der erste Wert in unserem Datensatz war also 18, was einen Z-Score von (18 – 58,93) / 29,060 = -1,40857 hatte.

Das bedeutet, dass der Wert „18“ 1,40857 Standardabweichungen unter dem Mittelwert liegt.

Umgekehrt war der letzte Wert in unseren Daten 108, was einem Z-Score von (108 – 58,93) / 29,060 = 1,68845 entsprach.

Das bedeutet, dass der Wert „108“ 1,68845 Standardabweichungen über dem Mittelwert liegt.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere häufige Aufgaben in SPSS ausführen:

So berechnen Sie deskriptive Statistiken für Variablen in SPSS
So berechnen Sie eine fünfstellige Zusammenfassung in SPSS
So identifizieren Sie Ausreißer in SPSS