Was ist ein modifizierter z-score? (definition & #038; beispiel)

In der Statistik sagt uns ein Z-Score , wie viele Standardabweichungen ein Wert vom Mittelwert hat. Wir verwenden die folgende Formel, um einen Z-Score zu berechnen:

Z-Score = (x _i – μ) / σ

Gold:

• x _i : ein einzelner Datenwert
• μ: der Durchschnitt des Datensatzes
• σ: die Standardabweichung des Datensatzes

Z-Scores werden häufig verwendet, um Ausreißer in einem Datensatz zu erkennen. Beispielsweise werden Beobachtungen mit einem Z-Score von weniger als -3 oder mehr als 3 oft als Ausreißer betrachtet.

Z-Scores können jedoch durch ungewöhnlich große oder kleine Datenwerte beeinflusst werden. Aus diesem Grund besteht eine robustere Möglichkeit zur Erkennung von Ausreißern darin, einen modifizierten Z-Score zu verwenden, der wie folgt berechnet wird:

Modifizierter Z-Score = 0,6745 (x _i – x̃) / MAD

Gold:

• x _i : ein einzelner Datenwert
• x̃: Der Median des Datensatzes
• MAD: die mittlere absolute Abweichung des Datensatzes

Ein modifizierter Z-Score ist robuster, da er den Median zur Berechnung der Z-Scores verwendet, im Gegensatz zum Mittelwert, der bekanntermaßen durch Ausreißer beeinflusst wird .

Iglewicz und Hoaglin empfehlen, Werte mit modifizierten Z-Scores von weniger als -3,5 oder mehr als 3,5 als potenzielle Ausreißer zu kennzeichnen.

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie modifizierte Z-Scores für einen bestimmten Datensatz berechnet werden.

Schritt 1: Erstellen Sie die Daten

Angenommen, wir haben den folgenden Datensatz mit 16 Werten:

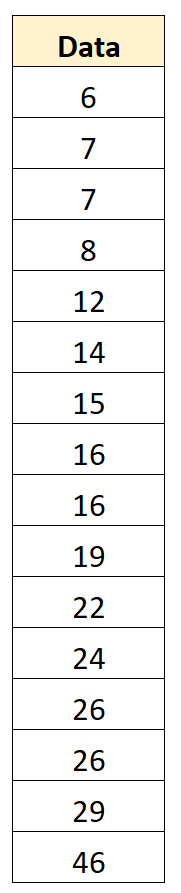
Schritt 2: Finden Sie den Median

Als nächstes ermitteln wir den Median. Dies stellt den Mittelpunkt des Datensatzes dar, der 16 beträgt.

Schritt 3: Ermitteln Sie die absolute Differenz zwischen jedem Wert und dem Median

Als nächstes ermitteln wir die absolute Differenz zwischen jedem einzelnen Datenwert und dem Median. Beispielsweise wird die absolute Differenz zwischen dem ersten Datenwert und dem Median wie folgt berechnet:

Absolute Differenz = |6 – 16| = 10

Mit derselben Formel können wir die absolute Differenz zwischen jedem einzelnen Datenwert und dem Median berechnen:

Schritt 4: Ermitteln Sie die absolute mittlere Abweichung

Als nächstes ermitteln wir die absolute mittlere Abweichung. Dies ist der Median der zweiten Spalte, der 8 beträgt.

Schritt 5: Finden Sie den modifizierten Z-Score für jeden Datenwert

Schließlich können wir den modifizierten Z-Score für jeden Datenwert mithilfe der folgenden Formel berechnen:

Modifizierter Z-Score = 0,6745 (x _i – x̃) / MAD

Der modifizierte Z-Score für den ersten Datenwert wird beispielsweise wie folgt berechnet:

Modifizierter Z-Score = 0,6745*(6-16) / 8 = -0,843

Wir können diese Formel für jeden Wert im Datensatz wiederholen:

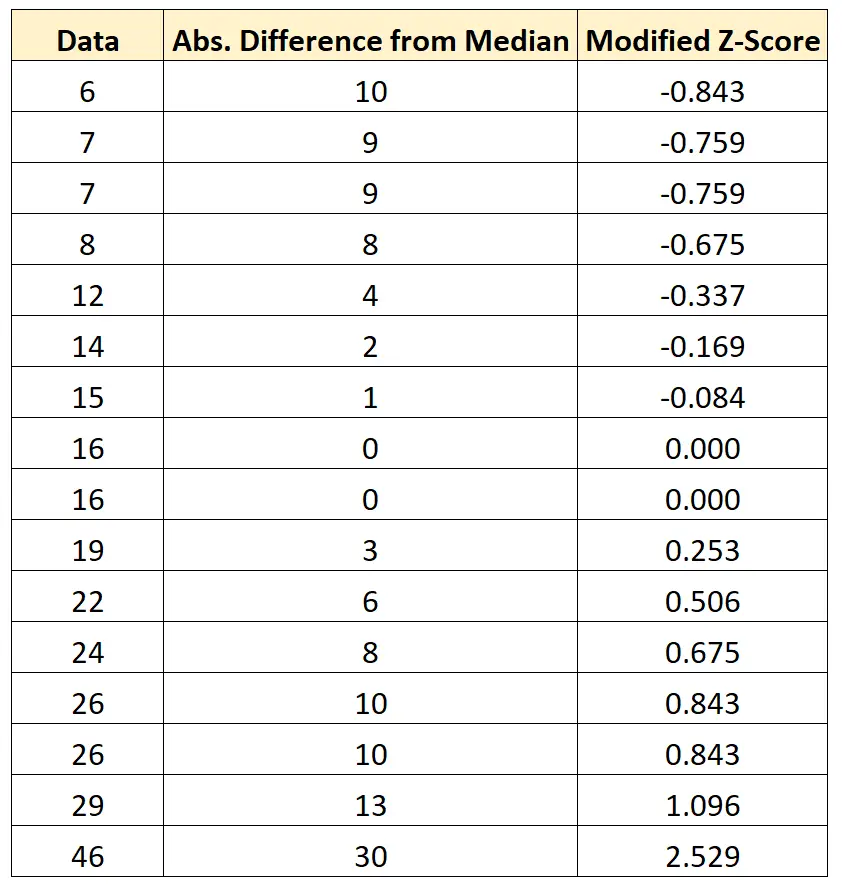
Wir können sehen, dass kein Wert im Datensatz einen modifizierten Z-Score von weniger als -3,5 oder mehr als 3,5 aufweist, daher kennzeichnen wir keinen Wert in diesem Datensatz als potenziellen Ausreißer.

Wie man mit Ausreißern umgeht

Wenn in Ihrem Datensatz ein Ausreißer vorhanden ist, haben Sie mehrere Möglichkeiten:

• Stellen Sie sicher, dass der Ausreißer nicht auf einen Dateneingabefehler zurückzuführen ist. Manchmal gibt eine Person beim Speichern der Daten einfach den falschen Datenwert ein. Wenn ein Ausreißer vorhanden ist, überprüfen Sie zunächst, ob der Wert korrekt eingegeben wurde und kein Fehler vorliegt.
• Weisen Sie dem Ausreißer einen neuen Wert zu . Wenn sich herausstellt, dass der Ausreißer das Ergebnis eines Dateneingabefehlers ist, können Sie ihm einen neuen Wert zuweisen, beispielsweise den Mittelwert oder Median des Datensatzes.
• Entfernen Sie den Ausreißer. Wenn es sich bei dem Wert wirklich um einen Ausreißer handelt, können Sie ihn entfernen, wenn er erhebliche Auswirkungen auf Ihre Gesamtanalyse hat. Erwähnen Sie in Ihrem Abschlussbericht oder Ihrer Analyse unbedingt, dass Sie einen Ausreißer entfernt haben.