So berechnen sie z-scores in sas

In der Statistik sagt uns ein Z-Score , wie viele Standardabweichungen ein Wert vom Mittelwert hat.

Wir verwenden die folgende Formel, um einen Z-Score zu berechnen:

z = (X – μ) / σ

Gold:

• X ist ein einzelner Rohdatenwert
• μ ist der Mittelwert des Datensatzes
• σ ist die Standardabweichung des Datensatzes

Das folgende Beispiel zeigt, wie Z-Scores für Rohdatenwerte in SAS berechnet werden.

Beispiel: Berechnen Sie Z-Scores in SAS

Angenommen, wir erstellen den folgenden Datensatz in SAS:

 /*create dataset*/
data original_data;
    input values;
    datalines ;
7
12
14
12
16
18
6
7
14
17
19
22
24
13
17
12
;
run ;

/*view dataset*/
proc print data = original_data;

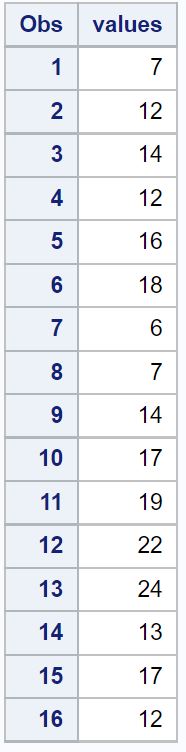
Nehmen wir nun an, wir möchten den Z-Score für jeden Wert im Datensatz berechnen.

Wir können dazu proc sql verwenden:

 /*create new variable that shows z-scores for each raw data value*/
proc sql ;
    select values, (values - mean(values)) / std(values) as z_scores
    from original_data;
quit ; 

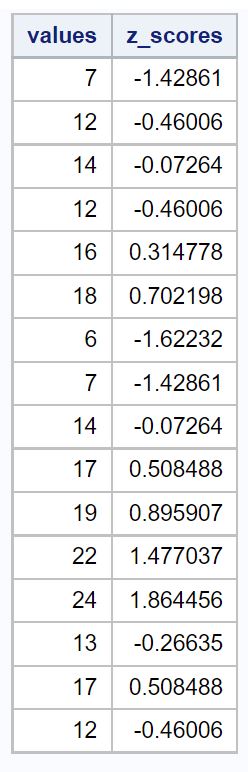
In der Spalte „Werte“ werden die ursprünglichen Datenwerte angezeigt, und in der Spalte „z_scores “ wird der Z-Score für jeden Wert angezeigt.

So interpretieren Sie Z-Scores in SAS

Ein Z-Score sagt uns, wie viele Standardabweichungen ein Wert vom Mittelwert hat.

Ein Z-Score kann positiv, negativ oder null sein.

Ein positiver Z-Score gibt an, dass ein bestimmter Wert über dem Durchschnitt liegt, ein negativer Z-Score zeigt an, dass ein bestimmter Wert unter dem Durchschnitt liegt, und ein Z-Score von Null zeigt an, dass ein bestimmter Wert dem Durchschnitt entspricht.

Wenn wir den Mittelwert und die Standardabweichung unseres Datensatzes berechnen würden, würden wir feststellen, dass der Mittelwert 14,375 und die Standardabweichung 5,162 beträgt.

Der erste Wert in unserem Datensatz war also 7, was einen Z-Score von (7-14,375) / 5,162 = -1,428 hatte. Das bedeutet, dass der Wert „7“ 1,428 Standardabweichungen niedriger ist als der Mittelwert.

Der nächste Wert in unseren Daten, 12, hatte einen Z-Score von (12-14,375) / 5,162 = -0,46 . Das bedeutet, dass der Wert „12“ 0,46 Standardabweichungen niedriger ist als der Mittelwert.

Je weiter ein Wert vom Mittelwert entfernt ist, desto höher ist der absolute Wert des Z-Scores für diesen Wert.

Beispielsweise ist der Wert 7 weiter vom Mittelwert (14,375) entfernt als der Wert 12, was erklärt, warum 7 einen Z-Score mit einem größeren Absolutwert hatte.

Zusätzliche Ressourcen

In den folgenden Artikeln wird erläutert, wie Sie andere häufige Aufgaben in SAS ausführen:

So identifizieren Sie Ausreißer in SAS
So berechnen Sie Perzentile in SAS
So berechnen Sie Mittelwert, Median und Modus in SAS