So zeichnen sie mehrere lineare regressionsergebnisse in r auf

Wenn wir eine einfache lineare Regression in R durchführen, ist es einfach, die angepasste Regressionslinie zu visualisieren, da wir nur mit einer einzigen Prädiktorvariablen und einer einzigen Antwortvariablen arbeiten.

Der folgende Code zeigt beispielsweise, wie man ein einfaches lineares Regressionsmodell an einen Datensatz anpasst und die Ergebnisse grafisch darstellt:

 #create dataset
data <- data.frame(x = c(1, 1, 2, 4, 4, 5, 6, 7, 7, 8, 9, 10, 11, 11),
                   y = c(13, 14, 17, 23, 24, 25, 25, 24, 28, 32, 33, 35, 40, 41))

#fit simple linear regression model
model <- lm(y ~ x, data = data)

#create scatterplot of data
plot(data$x, data$y)

#add fitted regression line
abline(model)

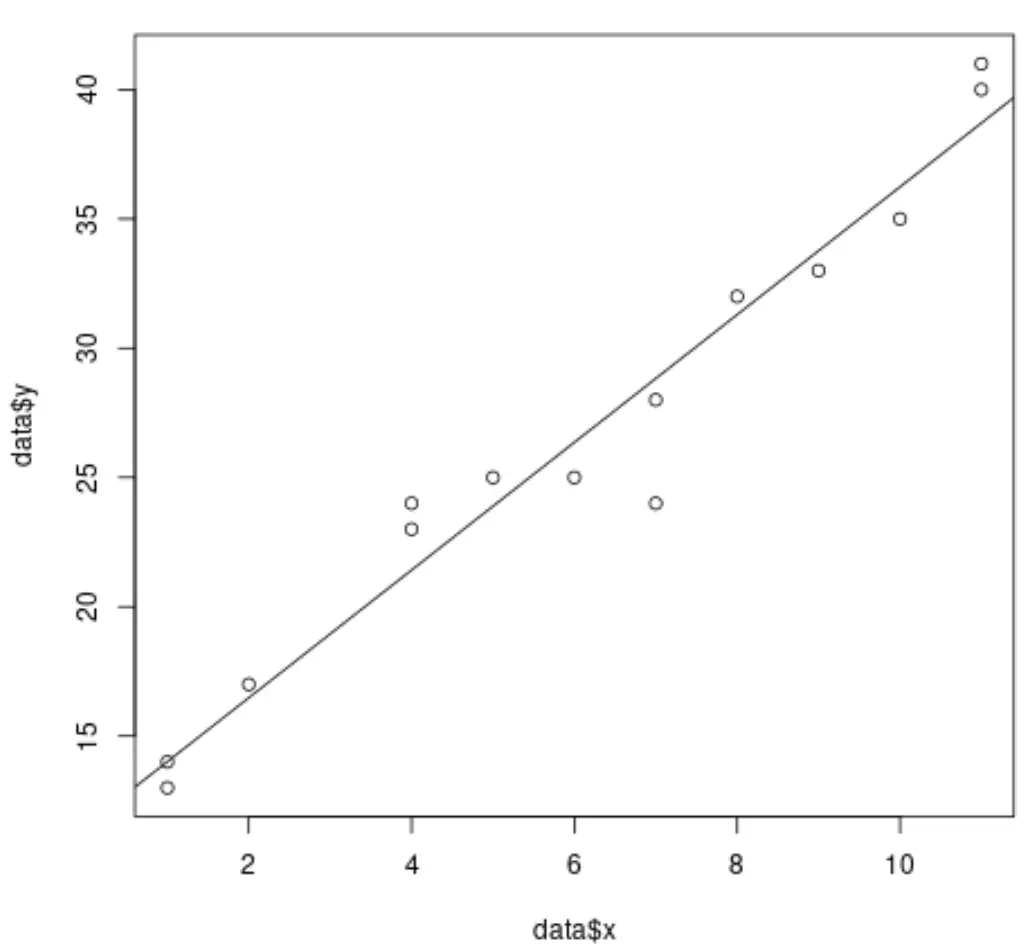
Wenn wir jedoch eine multiple lineare Regression durchführen, wird es schwierig, die Ergebnisse zu visualisieren, da es mehrere Prädiktorvariablen gibt und wir nicht einfach eine Regressionslinie in einem 2D-Diagramm zeichnen können.

Stattdessen können wir Diagramme hinzugefügter Variablen (manchmal auch „partielle Regressionsdiagramme“ genannt) verwenden, bei denen es sich um einzelne Diagramme handelt, die die Beziehung zwischen der Antwortvariablen und einer Prädiktorvariablen anzeigen und gleichzeitig das Vorhandensein anderer Prädiktorvariablen im Modell kontrollieren .

Das folgende Beispiel zeigt, wie man eine multiple lineare Regression in R durchführt und die Ergebnisse mithilfe angehängter Variablendiagramme visualisiert.

Beispiel: Plotten mehrerer linearer Regressionsergebnisse in R

Angenommen, wir passen das folgende multiple lineare Regressionsmodell mithilfe des integrierten mtcars- Datensatzes an einen Datensatz in R an:

 #fit multiple linear regression model
model <- lm(mpg ~ disp + hp + drat, data = mtcars)

#view results of model
summary(model)

Call:
lm(formula = mpg ~ disp + hp + drat, data = mtcars)

Residuals:
    Min 1Q Median 3Q Max 
-5.1225 -1.8454 -0.4456 1.1342 6.4958 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept) 19.344293 6.370882 3.036 0.00513 **
available -0.019232 0.009371 -2.052 0.04960 * 
hp -0.031229 0.013345 -2.340 0.02663 * 
drat 2.714975 1.487366 1.825 0.07863 . 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.008 on 28 degrees of freedom
Multiple R-squared: 0.775, Adjusted R-squared: 0.7509 
F-statistic: 32.15 on 3 and 28 DF, p-value: 3.28e-09

Aus den Ergebnissen können wir ersehen, dass der p-Wert für jeden der Koeffizienten kleiner als 0,1 ist. Der Einfachheit halber gehen wir davon aus, dass jede der Prädiktorvariablen signifikant ist und in das Modell einbezogen werden sollte.

Um Diagramme angehängter Variablen zu erstellen, können wir die Funktion avPlots() aus dem Paket car verwenden:

 #load car package
library(car)

#produce added variable plots
avPlots(model)

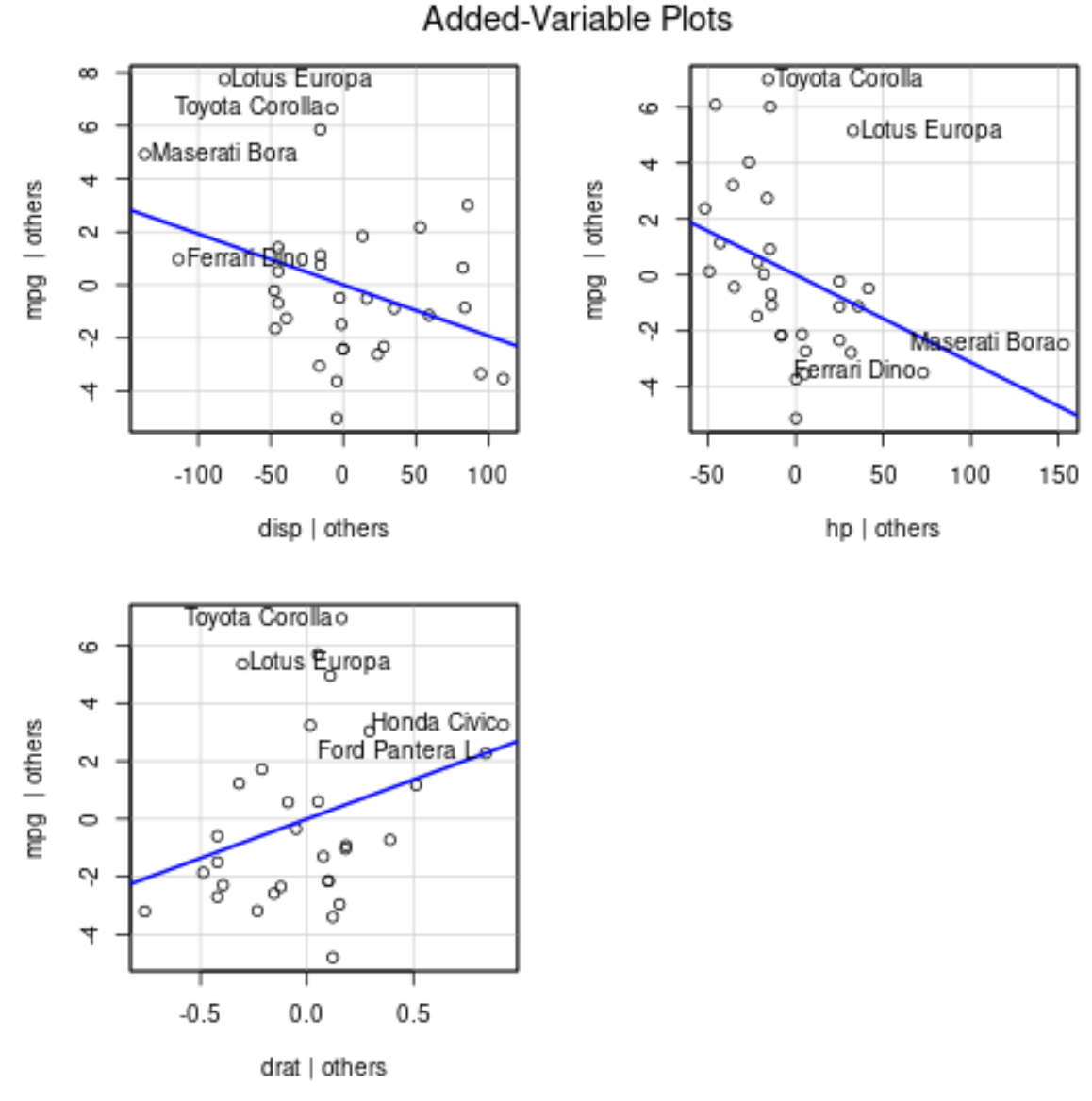
So interpretieren Sie jede Handlung:

• Die x-Achse zeigt eine einzelne Prädiktorvariable und die y-Achse zeigt die Antwortvariable an.
• Die blaue Linie zeigt den Zusammenhang zwischen der Prädiktorvariablen und der Antwortvariablen, während der Wert aller anderen Prädiktorvariablen konstant bleibt .
• Die beschrifteten Punkte in jedem Diagramm stellen die beiden Beobachtungen mit den größten Residuen und die beiden Beobachtungen mit der größten teilweisen Hebelwirkung dar.

Beachten Sie, dass der Winkel der Linie in jedem Diagramm dem Vorzeichen des Koeffizienten der geschätzten Regressionsgleichung entspricht.

Hier sind beispielsweise die geschätzten Koeffizienten für jede Prädiktorvariable im Modell:

• Anzeige: -0,019232
• ch: -0,031229
• Datum: 2.714975

Beachten Sie, dass der Winkel der Linie im Diagramm der hinzugefügten Variablen für drat positiv ist, während er für disp und hp negativ ist, was den Vorzeichen ihrer geschätzten Koeffizienten entspricht:

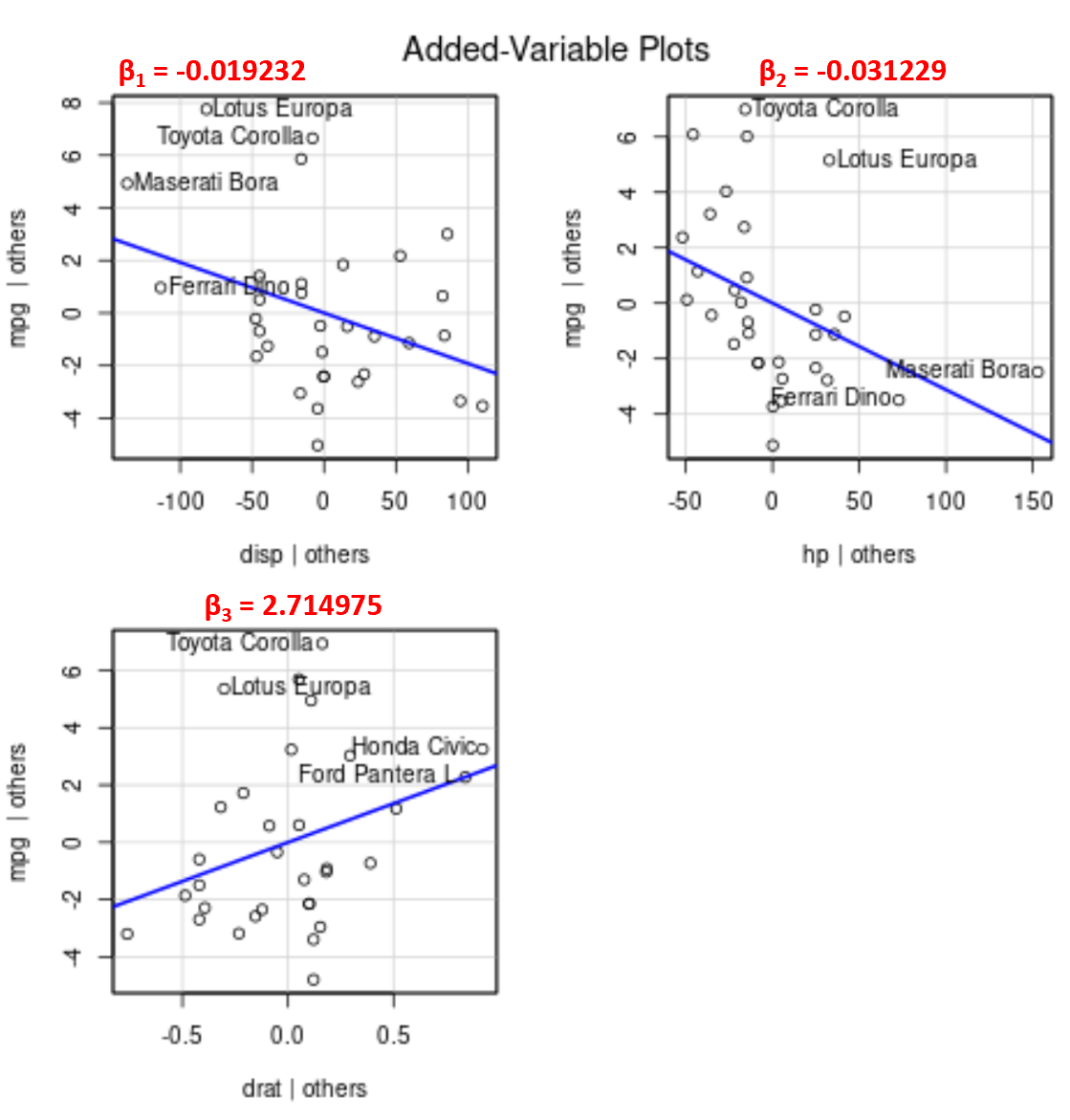
Obwohl wir keine einzelne angepasste Regressionslinie in einem 2D-Diagramm darstellen können, da wir über mehrere Prädiktorvariablen verfügen, ermöglichen uns diese hinzugefügten Variablendiagramme, die Beziehung zwischen jeder einzelnen Prädiktorvariablen und der Antwortvariablen zu beobachten und gleichzeitig die anderen Vorhersagevariablen konstant zu halten.