Zentraler grenzwertsatz

In diesem Artikel wird erläutert, was der zentrale Grenzwertsatz (CLT) ist und wofür er in der Statistik verwendet wird. Außerdem finden Sie die Formel des zentralen Grenzwertsatzes und ein Beispiel für seine Anwendung, das Schritt für Schritt gelöst wird.

Was ist der zentrale Grenzwertsatz?

In der Statistik besagt der Zentrale Grenzwertsatz , auch zentraler Grenzwertsatz genannt, dass sich die Verteilung der Stichprobenmittelwerte einer Normalverteilung annähert, wenn die Stichprobengröße zunimmt, unabhängig von der Wahrscheinlichkeitsverteilung der Grundgesamtheit.

Das heißt, der zentrale Grenzwertsatz besagt, dass der Mittelwert dieser Stichproben einer Normalverteilung angenähert werden kann, wenn wir eine ausreichend große Anzahl von Stichproben nehmen.

Darüber hinaus besagt der zentrale Grenzwertsatz, dass sich der Stichprobenmittelwert mit zunehmender Stichprobengröße dem Wert des Grundgesamtheitsmittelwerts annähert. Dadurch können wir die Parameter der statistischen Grundgesamtheit annähern. Im Folgenden werden wir sehen, wie das geht.

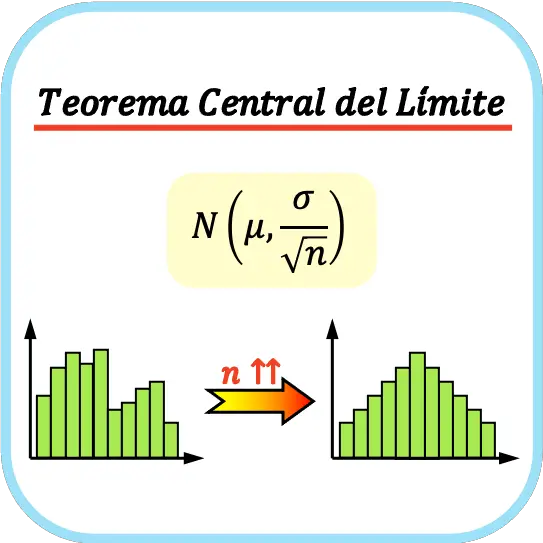
Im Allgemeinen wird davon ausgegangen, dass zur Anwendung des zentralen Grenzwertsatzes die Stichprobengröße mindestens 30 Beobachtungen betragen muss, obwohl dies von den Eigenschaften der untersuchten Variablen abhängt.

Der zentrale Grenzwertsatz hat viele Anwendungen, da die Normalverteilung inferenzielle statistische Berechnungen wie Hypothesentests oder Konfidenzintervalle ermöglicht. Im Finanzwesen wird beispielsweise der zentrale Grenzwertsatz verwendet, um die Rendite und das Risiko einer Investition zu analysieren.

Beispiel für den zentralen Grenzwertsatz

Nachdem wir die Definition des zentralen Grenzwertsatzes gesehen haben, schauen wir uns ein Beispiel an, um seine Bedeutung vollständig zu verstehen.

Ein Beispiel für den zentralen Grenzwertsatz ist das Würfeln. Der Würfelwurf folgt einer diskreten Gleichverteilung , da alle Ergebnisse gleichwahrscheinlich sind. Die Verteilung der Summe mehrerer Ergebnisse nähert sich jedoch einer Normalverteilung an.

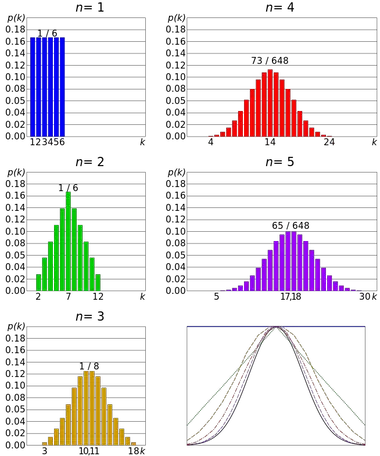
Je mehr Würfe es gibt, desto wahrscheinlicher ist es, dass die Form der Mittelwertverteilung eher dem Diagramm der Normalverteilung ähnelt.

Formel des zentralen Grenzwertsatzes

Der zentrale Grenzwertsatz besagt, dass, wenn eine Grundgesamtheit einen Mittelwert μ und eine Standardabweichung σ hat und wir eine ausreichend große Anzahl von Stichproben (n≥30) nehmen, die Menge der Stichprobenmittelwerte an eine Normalverteilung mit Mittelwert μ und Standardabweichung σ angenähert werden kann /√n.

Wenn außerdem X _{1 ,} zu einer Normalverteilung, die durch die _folgende Formel definiert ist:

Gelöste Übung des zentralen Grenzwertsatzes

Damit Sie sich das Konzept vollständig aneignen können, finden Sie hier eine gelöste Übung zum zentralen Grenzwertsatz.

• Ein Unternehmen verkauft Teile, die als Ersatz für bestimmte Spielzeugkomponenten dienen. Eine Münze hat ein durchschnittliches Gewicht von 300 g und eine Standardabweichung von 50 g. Wenn ein Kunde eine Charge von 100 Stück bestellt, wie hoch ist die Wahrscheinlichkeit, dass das durchschnittliche Gewicht der Stücke in der Charge mehr als 305 g beträgt? Und wie groß ist die Wahrscheinlichkeit, dass eine Charge von 100 Stück mehr als 31 kg wiegt?

Da die Chargengröße groß ist (n=100), können wir den zentralen Grenzwertsatz anwenden, um das Problem zu lösen.

Unter Verwendung der Formel des zentralen Grenzwertsatzes kann die Verteilung der Stichprobenmittelwerte somit einer Normalverteilung mit den folgenden Parametern angenähert werden:

Nun führen wir den Tippvorgang durch, um anschließend die Wahrscheinlichkeit zu ermitteln, die die Übung von uns verlangt. Dazu müssen wir den Mittelwert von der Verteilung subtrahieren und ihn dann durch die Standardabweichung dividieren:

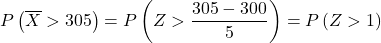Normalverteilungstabelle entspricht:

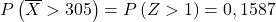
Also wiederholen wir den Eingabevorgang und ermitteln dann die zweite Wahrscheinlichkeit, mit der das Problem uns fragt:

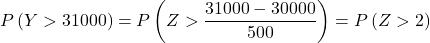
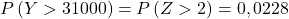➤ Siehe: Gesetz der großen Zahlen