So wenden sie den zentralen grenzwertsatz in excel an

Der zentrale Grenzwertsatz besagt, dass die Stichprobenverteilung eines Stichprobenmittelwerts annähernd normal ist, wenn die Stichprobengröße groß genug ist, auch wenn die Grundgesamtheitsverteilung nicht normal ist .

Der zentrale Grenzwertsatz besagt außerdem, dass die Stichprobenverteilung die folgenden Eigenschaften haben wird:

1. Der Mittelwert der Stichprobenverteilung entspricht dem Mittelwert der Bevölkerungsverteilung:

x = µ

2. Die Standardabweichung der Stichprobenverteilung entspricht der Standardabweichung der Grundgesamtheit dividiert durch die Stichprobengröße:

s = σ / √n

In diesem Tutorial erklären wir, wie man den zentralen Grenzwertsatz in Excel auf eine gegebene Verteilung anwendet.

Anwendung des Zentralen Grenzwertsatzes in Excel

Angenommen, wir haben eine Verteilung mit einem Mittelwert von 8 und einer Standardabweichung von 4 . Mit den folgenden Formeln in Excel können wir sowohl den Mittelwert als auch die Standardabweichung der Stichprobenverteilung bei einer Stichprobengröße von 15 ermitteln:

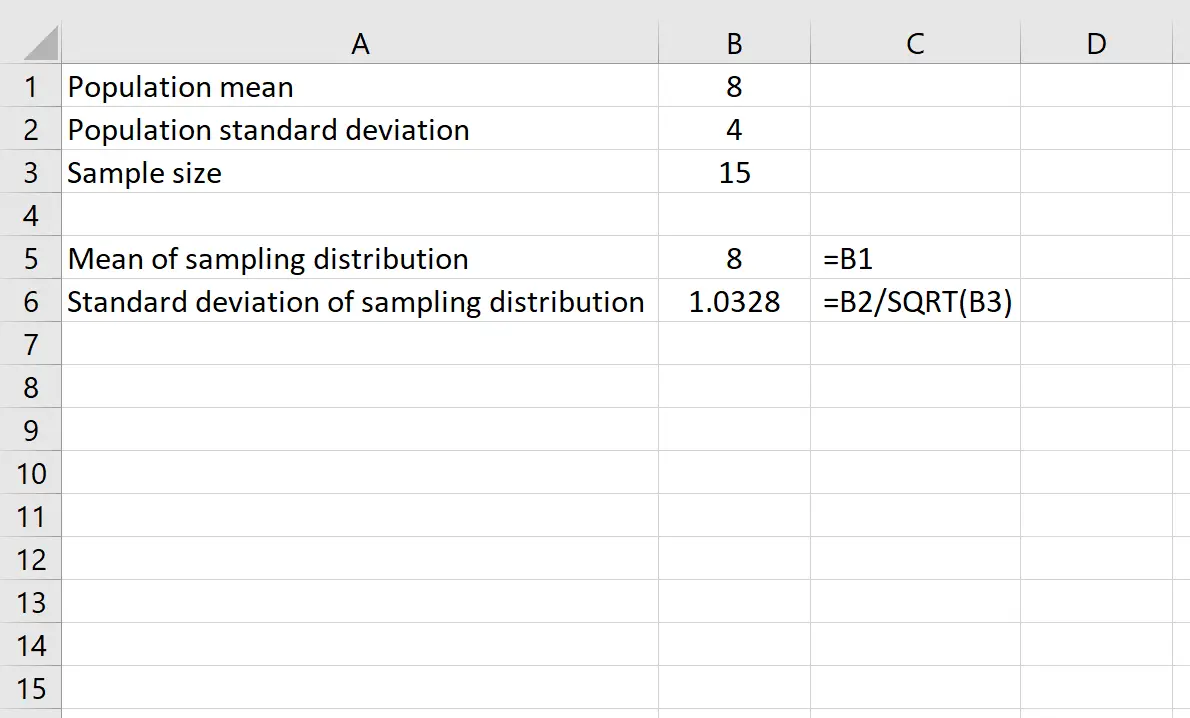
Der Mittelwert der Stichprobenverteilung ist einfach gleich dem Mittelwert der Bevölkerungsverteilung, der 8 beträgt.

Die Standardabweichung der Stichprobenverteilung entspricht der Grundgesamtheitsstandardabweichung dividiert durch die Stichprobengröße oder: 4 /√15 = 1,0328 .

Wir können den zentralen Grenzwertsatz auch verwenden, um Fragen zur Wahrscheinlichkeit zu beantworten. Wenn eine bestimmte Grundgesamtheit beispielsweise einen Mittelwert von 8 und eine Standardabweichung von 4 hat, wie hoch ist dann die Wahrscheinlichkeit, dass eine bestimmte Stichprobe die Größe 15 hat?   hat einen Durchschnitt kleiner oder gleich 7 ?

Um diese Frage zu beantworten, können wir die Funktion NORM.DIST() in Excel verwenden, die die folgende Syntax verwendet:

NORM.DIST(x, Durchschnitt, Standard_Abteilung, kumulativ)

Gold:

• x: Beispiel bedeutet, dass Sie testen möchten
• Mittelwert: erwarteter Mittelwert der Stichprobenverteilung
• standard_dev: erwartete Standardabweichung der Stichprobenverteilung
• kumulativ: TRUE gibt den normalen CDF-Wert zurück; FALSE gibt den Wert eines normalen PDF zurück. In unserem Fall verwenden wir immer TRUE.

Diese Funktion gibt die Wahrscheinlichkeit zurück, dass der Stichprobenmittelwert kleiner oder gleich einem bestimmten Wert ist.

Hier ist die Formel, die wir in diesem Beispiel verwenden würden:

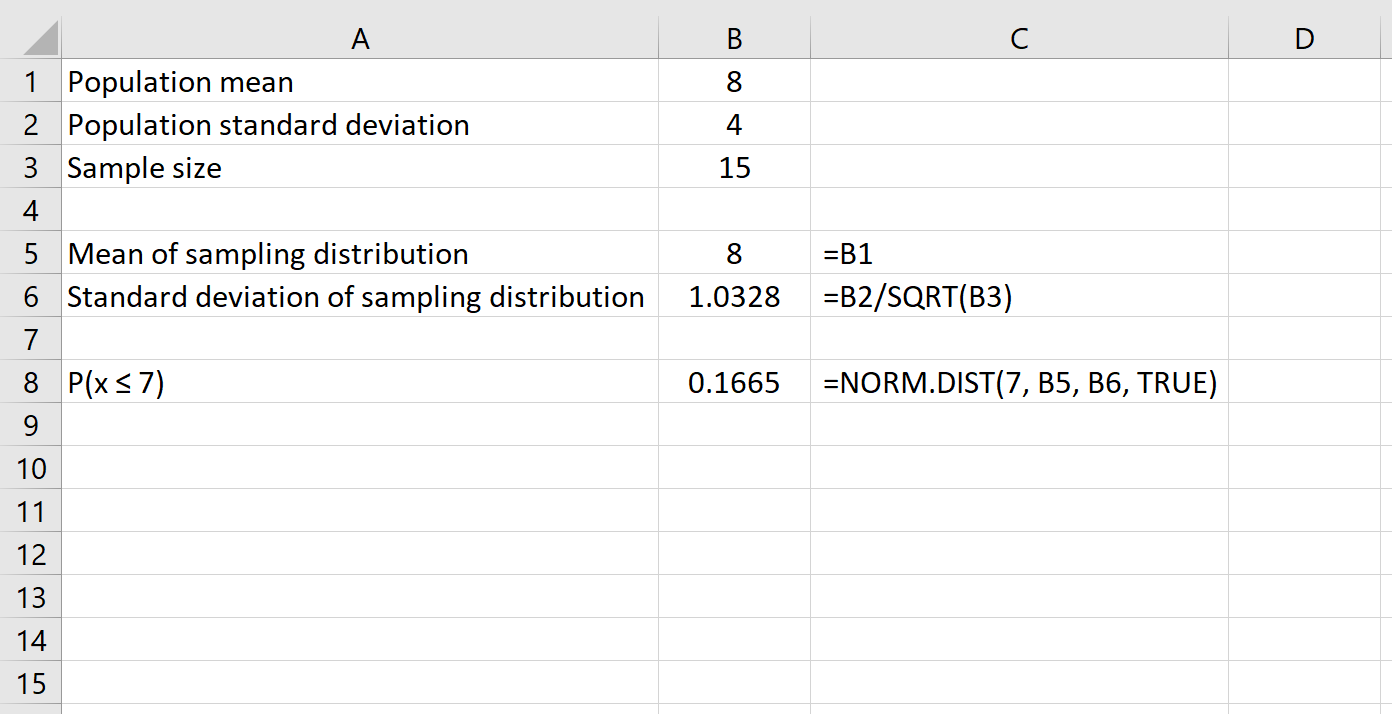
Dies sagt uns, dass für eine Grundgesamtheit mit einem Mittelwert von 8 und einer Standardabweichung von 4 die Wahrscheinlichkeit, dass eine gegebene Stichprobe eine Größe hat, 15 beträgt   hat einen Durchschnitt kleiner oder gleich 7 oder 0,1665 .

Wir können auch die Wahrscheinlichkeit ermitteln, dass eine bestimmte Stichprobengröße einen Mittelwert hat, der größer als eine bestimmte Zahl ist, indem wir einfach Formel 1 verwenden – NORM.DIST() .

Die folgende Formel zeigt beispielsweise, wie die Wahrscheinlichkeit bestimmt wird, dass eine gegebene Stichprobengröße von 15 einen Mittelwert größer als 7 aufweist:

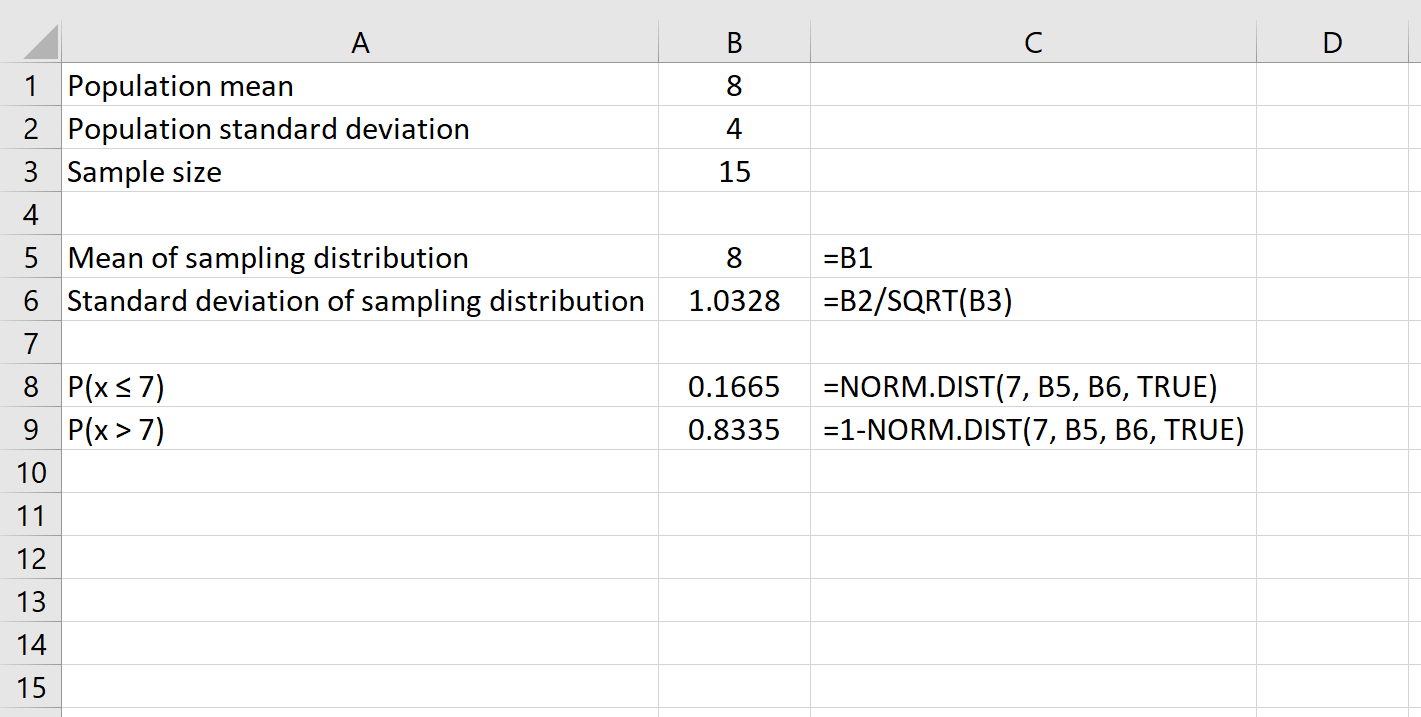
Schließlich können wir mithilfe der Formel NORM.VERT(größere Zahl) – NORM.VERT(kleinere Zahl) die Wahrscheinlichkeit ermitteln, dass eine bestimmte Stichprobengröße einen Mittelwert zwischen zwei Zahlen aufweist.

Die folgende Formel zeigt beispielsweise, wie man die Wahrscheinlichkeit ermittelt, dass eine gegebene Stichprobengröße von 15 einen Mittelwert zwischen 7 und 9 hat:

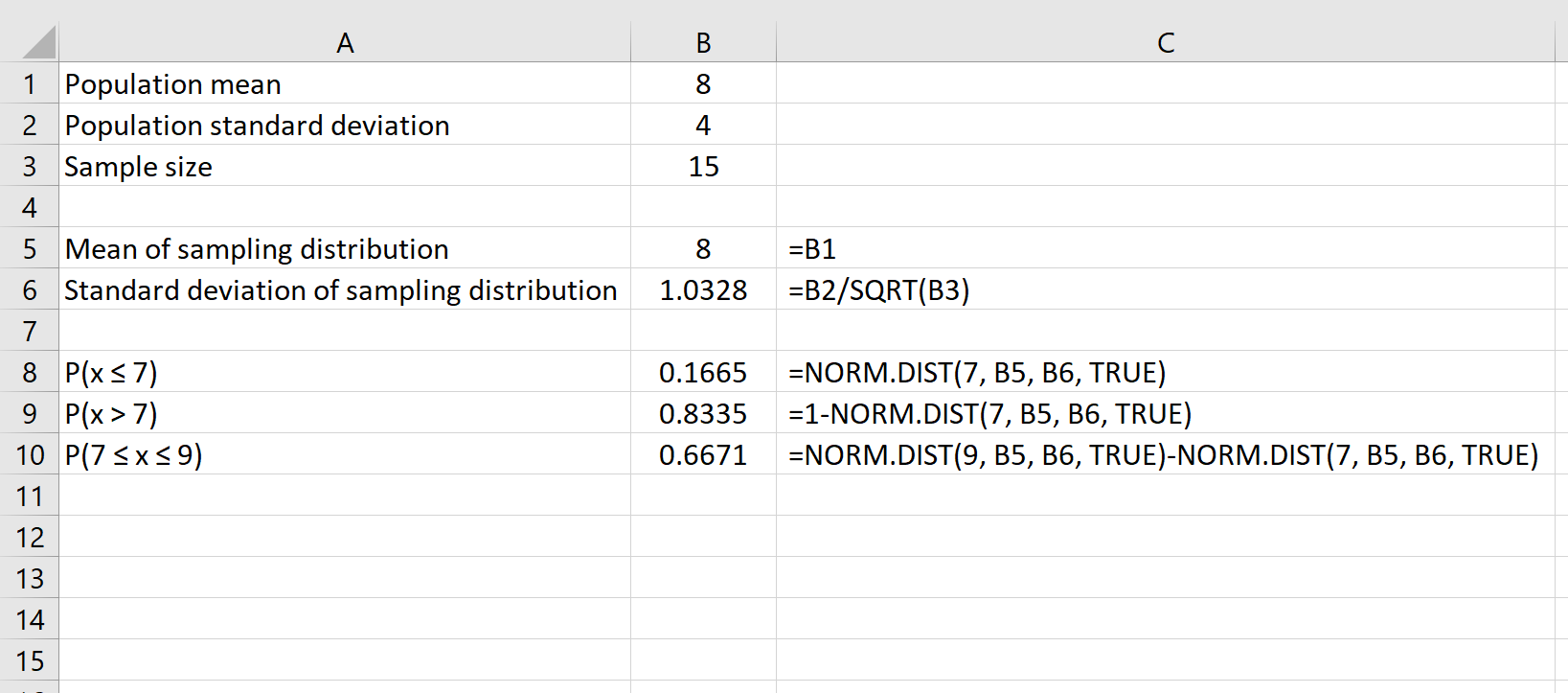
Zusätzliche Ressourcen

Zentraler Grenzwertsatz-Rechner
So wenden Sie die Faustregel in Excel an
So erstellen Sie eine Glockenkurve in Excel