So wenden sie den zentralen grenzwertsatz in r an (mit beispielen)

Der zentrale Grenzwertsatz besagt, dass die Stichprobenverteilung eines Stichprobenmittelwerts annähernd normal ist, wenn die Stichprobengröße groß genug ist, auch wenn die Grundgesamtheitsverteilung nicht normal ist.

Der zentrale Grenzwertsatz besagt außerdem, dass die Stichprobenverteilung die folgenden Eigenschaften haben wird:

1. Der Mittelwert der Stichprobenverteilung entspricht dem Mittelwert der Bevölkerungsverteilung:

x = µ

2. Die Standardabweichung der Stichprobenverteilung entspricht der Standardabweichung der Grundgesamtheitsverteilung dividiert durch die Stichprobengröße:

s = σ /n

Das folgende Beispiel zeigt, wie der zentrale Grenzwertsatz in R angewendet wird.

Beispiel: Anwendung des zentralen Grenzwertsatzes in R

Angenommen, die Breite des Panzers einer Schildkröte folgt einer gleichmäßigen Verteilung mit einer minimalen Breite von 2 Zoll und einer maximalen Breite von 6 Zoll.

Das heißt, wenn wir eine Schildkröte zufällig auswählen und die Breite ihres Panzers messen, ist es wahrscheinlich, dass sie auch zwischen 2 und 6 Zoll breit ist.

Der folgende Code zeigt, wie man in R einen Datensatz erstellt, der die Maße der Panzerbreite von 1.000 Schildkröten enthält, gleichmäßig verteilt zwischen 2 und 6 Zoll:

 #make this example reproducible
set. seeds (0)

#create random variable with sample size of 1000 that is uniformly distributed
data <- runif(n=1000, min=2, max=6)

#create histogram to visualize distribution of turtle shell widths
hist(data, col=' steelblue ', main=' Histogram of Turtle Shell Widths ')

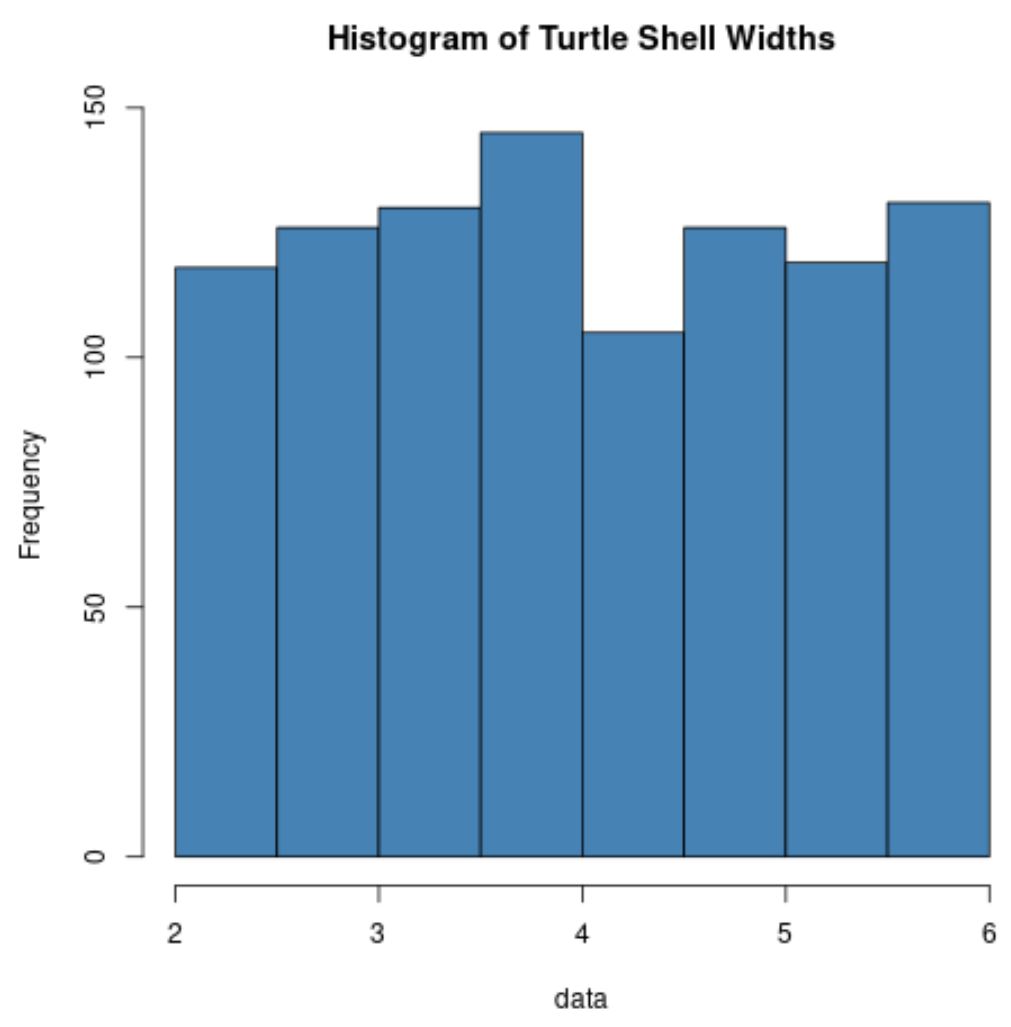
Beachten Sie, dass die Verteilung der Schildkrötenpanzerbreiten normalerweise überhaupt nicht verteilt ist.

Stellen Sie sich nun vor, wir nehmen wiederholt zufällige Stichproben von 5 Schildkröten aus dieser Population und messen den Stichprobenmittelwert immer wieder.

Der folgende Code zeigt, wie dieser Prozess in R durchgeführt und ein Histogramm erstellt wird, um die Verteilung der Stichprobenmittelwerte zu visualisieren:

 #create empty vector to hold sample means
sample5 <- c()

#take 1,000 random samples of size n=5
n = 1000
for (i in 1:n){
sample5[i] = mean(sample(data, 5, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample5)

[1] 4.008103

sd(sample5)

[1] 0.5171083 

#create histogram to visualize sampling distribution of sample means
hist(sample5, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 5 ') 

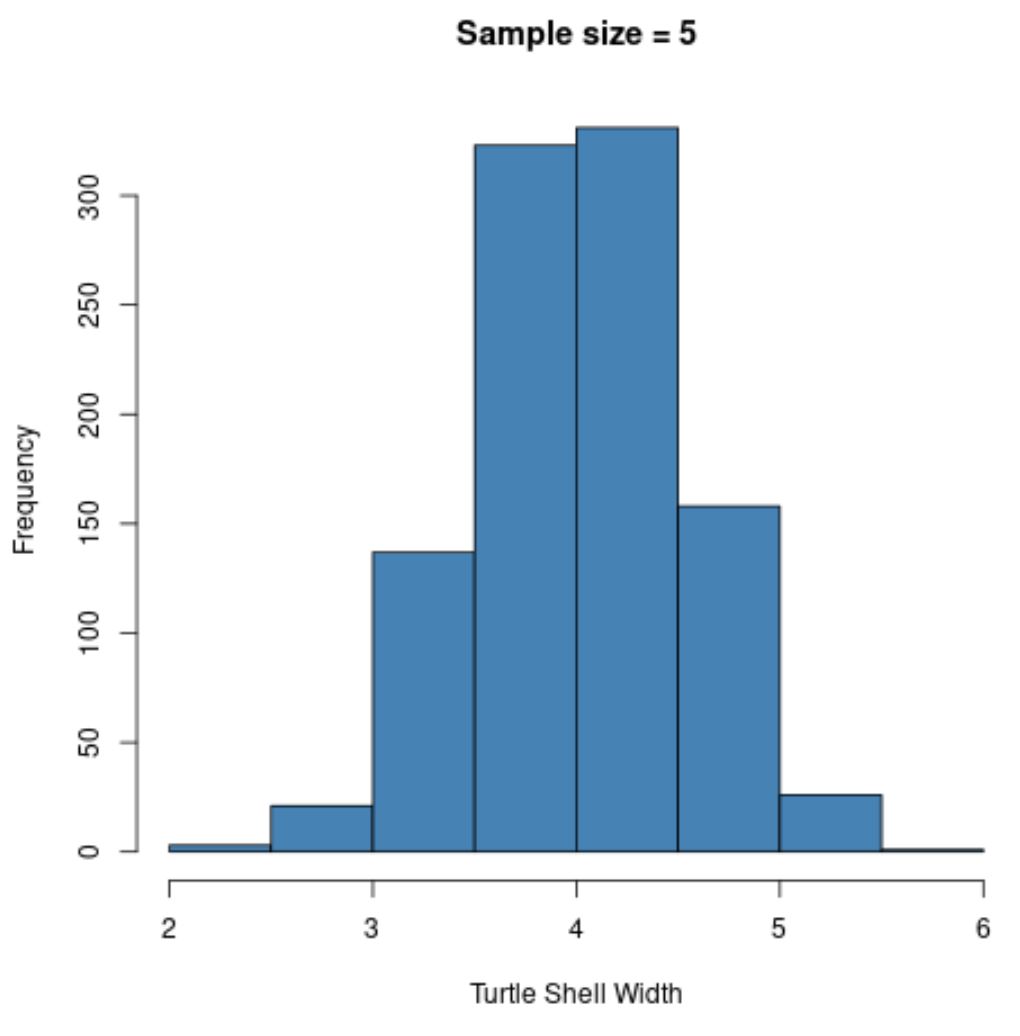
Beachten Sie, dass die Stichprobenverteilung der Stichprobenmittelwerte normalverteilt erscheint, obwohl die Verteilung, aus der die Stichproben stammten, nicht normalverteilt war.

Beachten Sie auch den Stichprobenmittelwert und die Stichprobenstandardabweichung für diese Stichprobenverteilung:

• x̄ : 4,008
• s : 0,517

Nehmen wir nun an, wir erhöhen die Stichprobengröße, die wir verwenden, von n=5 auf n=30 und erstellen das Histogramm der Stichprobenmittelwerte neu:

 #create empty vector to hold sample means
sample30 <- c()

#take 1,000 random samples of size n=30
n = 1000
for (i in 1:n){
sample30[i] = mean(sample(data, 30, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample30)

[1] 4.000472

sd(sample30)

[1] 0.2003791

#create histogram to visualize sampling distribution of sample means
hist(sample30, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 30 ') 

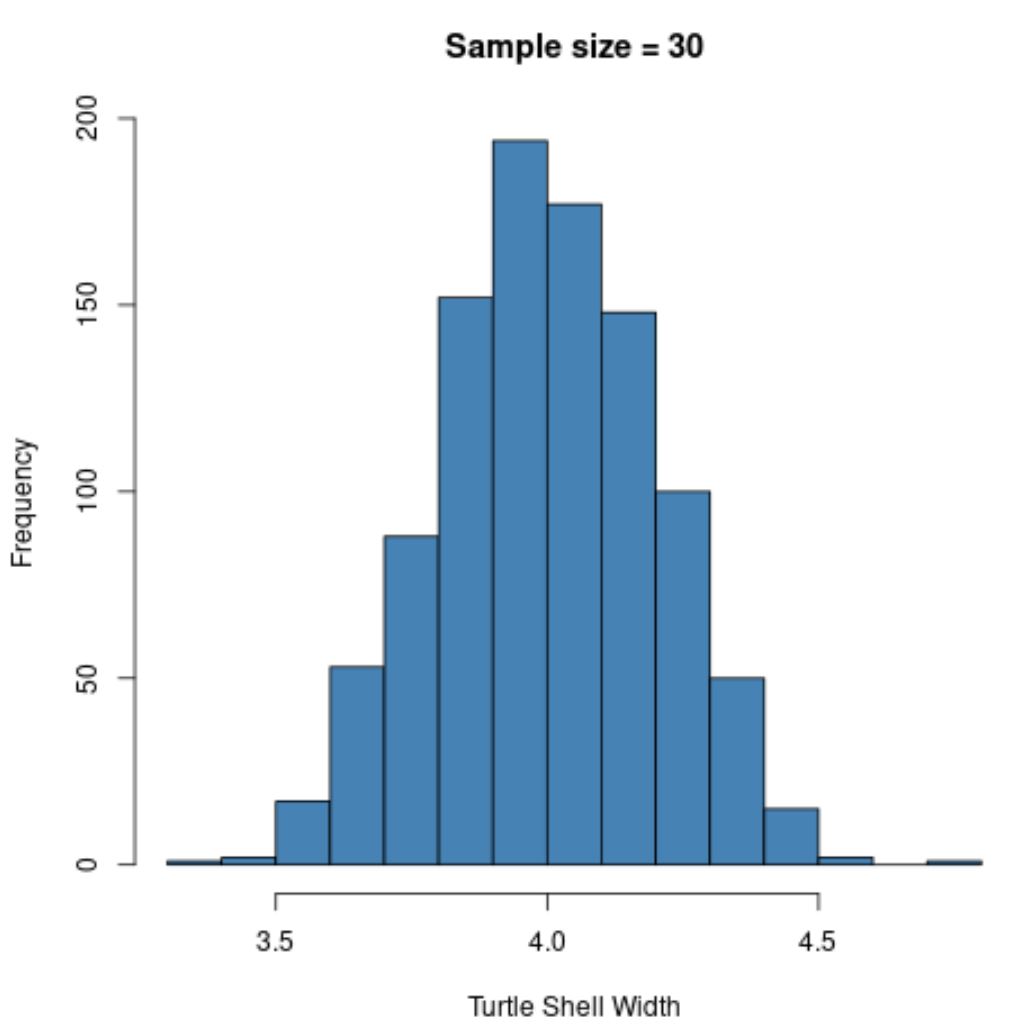
Die Stichprobenverteilung ist wiederum normalverteilt , die Stichprobenstandardabweichung ist jedoch noch kleiner:

• s : 0,200

Dies liegt daran, dass wir im Vergleich zum vorherigen Beispiel (n=5) eine größere Stichprobengröße (n=30) verwendet haben, sodass die Standardabweichung der Stichprobenmittelwerte noch kleiner ist.

Wenn wir weiterhin immer größere Stichproben verwenden, werden wir feststellen, dass die Stichprobenstandardabweichung immer kleiner wird.

Dies veranschaulicht den zentralen Grenzwertsatz in der Praxis.

Zusätzliche Ressourcen

Die folgenden Ressourcen bieten zusätzliche Informationen zum zentralen Grenzwertsatz:

Eine Einführung in den zentralen Grenzwertsatz
Zentraler Grenzwertsatz-Rechner
5 Beispiele für die Anwendung des zentralen Grenzwertsatzes im wirklichen Leben