So wenden sie den zentralen grenzwertsatz auf den ti-84-rechner an

Der zentrale Grenzwertsatz besagt, dass die Stichprobenverteilung eines Stichprobenmittelwerts annähernd normal ist, wenn die Stichprobengröße groß genug ist, auch wenn die Grundgesamtheitsverteilung nicht normal ist.

Der zentrale Grenzwertsatz besagt außerdem, dass die Stichprobenverteilung die folgenden Eigenschaften haben wird:

1. Der Mittelwert der Stichprobenverteilung entspricht dem Mittelwert der Bevölkerungsverteilung:

x = µ

2. Die Standardabweichung der Stichprobenverteilung entspricht der Standardabweichung der Grundgesamtheit dividiert durch die Stichprobengröße:

s = σ / √n

Um die Wahrscheinlichkeiten im Zusammenhang mit dem Stichprobenmittelwert auf einem TI-84-Rechner zu ermitteln, können wir die Funktion normalcdf() mit der folgenden Syntax verwenden:

 normalcdf (lower value, upper value, x , s/√ n )

Gold:

• x : Stichprobenmittel
• s : Stichprobenstandardabweichung
• n : Stichprobengröße

Um auf diese Funktion auf einem TI-84-Rechner zuzugreifen, drücken Sie einfach 2nd und dann VARS , scrollen Sie dann zu normalcdf ( und drücken Sie ENTER .

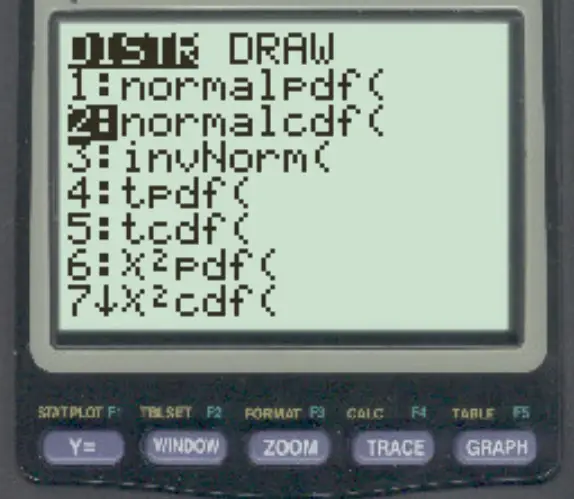
Die folgenden Beispiele zeigen, wie Sie diese Funktion in der Praxis nutzen können.

Beispiel 1: Finden Sie die Wahrscheinlichkeit zwischen zwei Werten

Eine Verteilung hat einen Mittelwert von 70 und eine Standardabweichung von 7. Wenn wir eine Zufallsstichprobe mit der Größe n = 35 auswählen, ermitteln Sie die Wahrscheinlichkeit, dass der Stichprobenmittelwert zwischen 68 und 72 liegt.

Wir können die folgende Syntax auf dem TI-84 verwenden:

 normalcdf (68, 72, 70, 7/√ 35 ) 

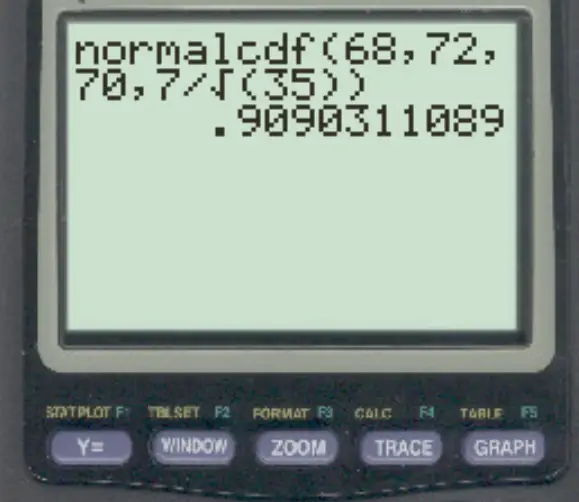
Die Wahrscheinlichkeit, dass der Stichprobenmittelwert zwischen 68 und 72 liegt, beträgt 0,909 .

Beispiel 2: Finden einer Wahrscheinlichkeit, die größer als ein Wert ist

Eine Verteilung hat einen Mittelwert von 50 und eine Standardabweichung von 4. Wenn wir eine Zufallsstichprobe mit der Größe n = 30 auswählen, ermitteln Sie die Wahrscheinlichkeit, dass der Stichprobenmittelwert größer als 48 ist.

Wir können die folgende Syntax auf dem TI-84 verwenden:

 normalcdf (48, E99, 50, 4/√ 30 )

Hinweis: Sie können auf das „E“-Symbol zugreifen, indem Sie 2 drücken und dann die Taste , drücken.

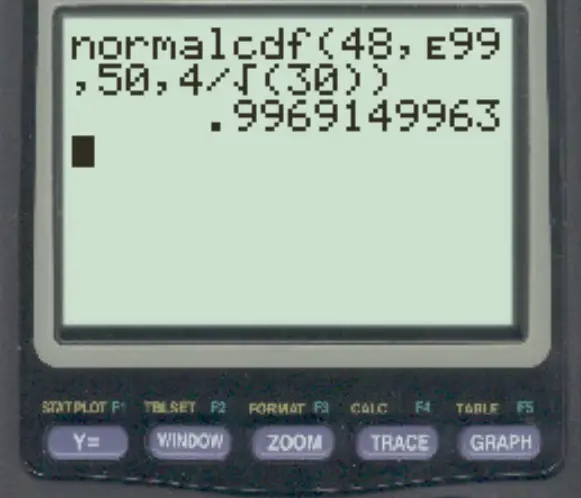
Die Wahrscheinlichkeit, dass der Stichprobenmittelwert größer als 48 ist, beträgt 0,9969 .

Beispiel 3: Finden einer Wahrscheinlichkeit, die kleiner als ein Wert ist

Eine Verteilung hat einen Mittelwert von 20 und eine Standardabweichung von 3. Wenn wir eine Zufallsstichprobe mit der Größe n = 40 auswählen, ermitteln Sie die Wahrscheinlichkeit, dass der Stichprobenmittelwert kleiner als 19 ist.

Wir können die folgende Syntax auf dem TI-84 verwenden:

 normalcdf (-E99, 19, 20, 3/√ 40 ) 

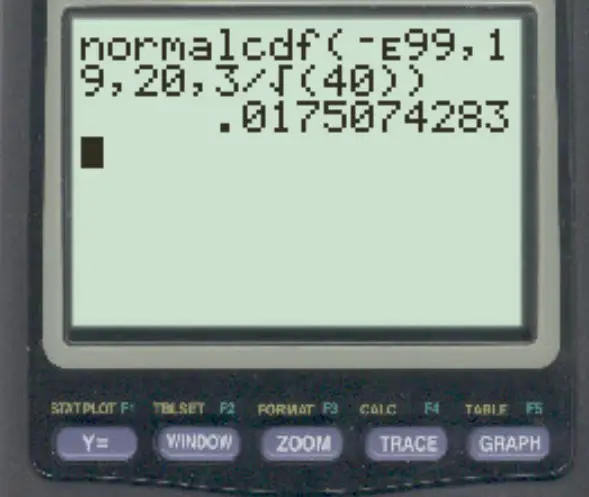
Die Wahrscheinlichkeit, dass der Stichprobenmittelwert kleiner als 19 ist, beträgt 0,0175 .

Zusätzliche Ressourcen

Eine Einführung in den zentralen Grenzwertsatz
Zentraler Grenzwertsatz-Rechner
So wenden Sie den zentralen Grenzwertsatz in Excel an
Zentraler Grenzwertsatz: die vier zu erfüllenden Bedingungen