So erstellen sie zufällige wälder in r (schritt für schritt)

Wenn die Beziehung zwischen einer Reihe von Prädiktorvariablen und einer Antwortvariablen sehr komplex ist, verwenden wir häufig nichtlineare Methoden, um die Beziehung zwischen ihnen zu modellieren.

Eine solche Methode ist die Erstellung eines Entscheidungsbaums . Der Nachteil bei der Verwendung eines einzelnen Entscheidungsbaums besteht jedoch darin, dass er tendenziell unter einer hohen Varianz leidet.

Das heißt, wenn wir den Datensatz in zwei Hälften aufteilen und den Entscheidungsbaum auf beide Hälften anwenden, könnten die Ergebnisse sehr unterschiedlich ausfallen.

Eine Methode, mit der wir die Varianz eines einzelnen Entscheidungsbaums reduzieren können, besteht darin, ein Zufallswaldmodell zu erstellen, das wie folgt funktioniert:

1. Nehmen Sie b Bootstrapping-Beispiele aus dem Originaldatensatz.

2. Erstellen Sie einen Entscheidungsbaum für jedes Bootstrap-Beispiel.

• Bei der Erstellung des Baums wird jedes Mal, wenn eine Aufteilung in Betracht gezogen wird, nur eine Zufallsstichprobe von m Prädiktoren als Kandidaten für die Aufteilung aus dem gesamten Satz von p Prädiktoren betrachtet. Im Allgemeinen wählen wir m gleich √p .

3. Mitteln Sie die Vorhersagen jedes Baums, um ein endgültiges Modell zu erhalten.

Es stellt sich heraus, dass zufällige Wälder tendenziell viel genauere Modelle erzeugen als einzelne Entscheidungsbäume und sogar verpackte Modelle .

Dieses Tutorial bietet ein schrittweises Beispiel für die Erstellung eines Zufallsstrukturmodells für einen Datensatz in R.

Schritt 1: Laden Sie die erforderlichen Pakete

Zuerst laden wir die notwendigen Pakete für dieses Beispiel. Für dieses einfache Beispiel benötigen wir nur ein Paket:

 library (randomForest)

Schritt 2: Passen Sie das Random Forest-Modell an

Für dieses Beispiel verwenden wir einen integrierten R-Datensatz namens „Air Quality“ , der Messungen der Luftqualität in New York City über 153 einzelne Tage enthält.

 #view structure of air quality dataset
str(airquality)

'data.frame': 153 obs. of 6 variables:
 $ Ozone: int 41 36 12 18 NA 28 23 19 8 NA ...
 $Solar.R: int 190 118 149 313 NA NA 299 99 19 194 ...
 $ Wind: num 7.4 8 12.6 11.5 14.3 14.9 8.6 13.8 20.1 8.6 ...
 $ Temp: int 67 72 74 62 56 66 65 59 61 69 ...
 $Month: int 5 5 5 5 5 5 5 5 5 5 ...
 $Day: int 1 2 3 4 5 6 7 8 9 10 ...

#find number of rows with missing values
sum(! complete . cases (airquality))

[1] 42

Dieser Datensatz enthält 42 Zeilen mit fehlenden Werten. Bevor wir ein Zufallswaldmodell anpassen, füllen wir daher die fehlenden Werte in jeder Spalte mit den Spaltenmedianen auf:

 #replace NAs with column medians
for (i in 1: ncol (air quality)) {
  airquality[,i][ is . na (airquality[, i])] <- median (airquality[, i], na . rm = TRUE )
}

Verwandt: So unterstellen Sie fehlende Werte in R

Der folgende Code zeigt, wie man mithilfe der Funktion randomForest() aus dem Paket randomForest ein Zufallswaldmodell in R anpasst.

 #make this example reproducible
set.seed(1)

#fit the random forest model
model <- randomForest(
  formula = Ozone ~ .,
  data = airquality
)

#display fitted model
model

Call:
 randomForest(formula = Ozone ~ ., data = airquality) 
               Type of random forest: regression
                     Number of trees: 500
No. of variables tried at each split: 1

          Mean of squared residuals: 327.0914
                    % Var explained: 61

#find number of trees that produce lowest test MSE
which.min(model$mse)

[1] 82

#find RMSE of best model
sqrt(model$mse[ which . min (model$mse)]) 

[1] 17.64392

Aus dem Ergebnis können wir ersehen, dass das Modell, das den niedrigsten mittleren quadratischen Testfehler (MSE) erzeugte, 82 Bäume verwendete.

Wir können auch sehen, dass der quadratische Mittelfehler dieses Modells 17,64392 betrug. Wir können uns dies als die durchschnittliche Differenz zwischen dem vorhergesagten Wert für Ozon und dem tatsächlich beobachteten Wert vorstellen.

Wir können auch den folgenden Code verwenden, um einen Plot des MSE-Tests basierend auf der Anzahl der verwendeten Bäume zu erstellen:

 #plot the MSE test by number of trees
plot(model)

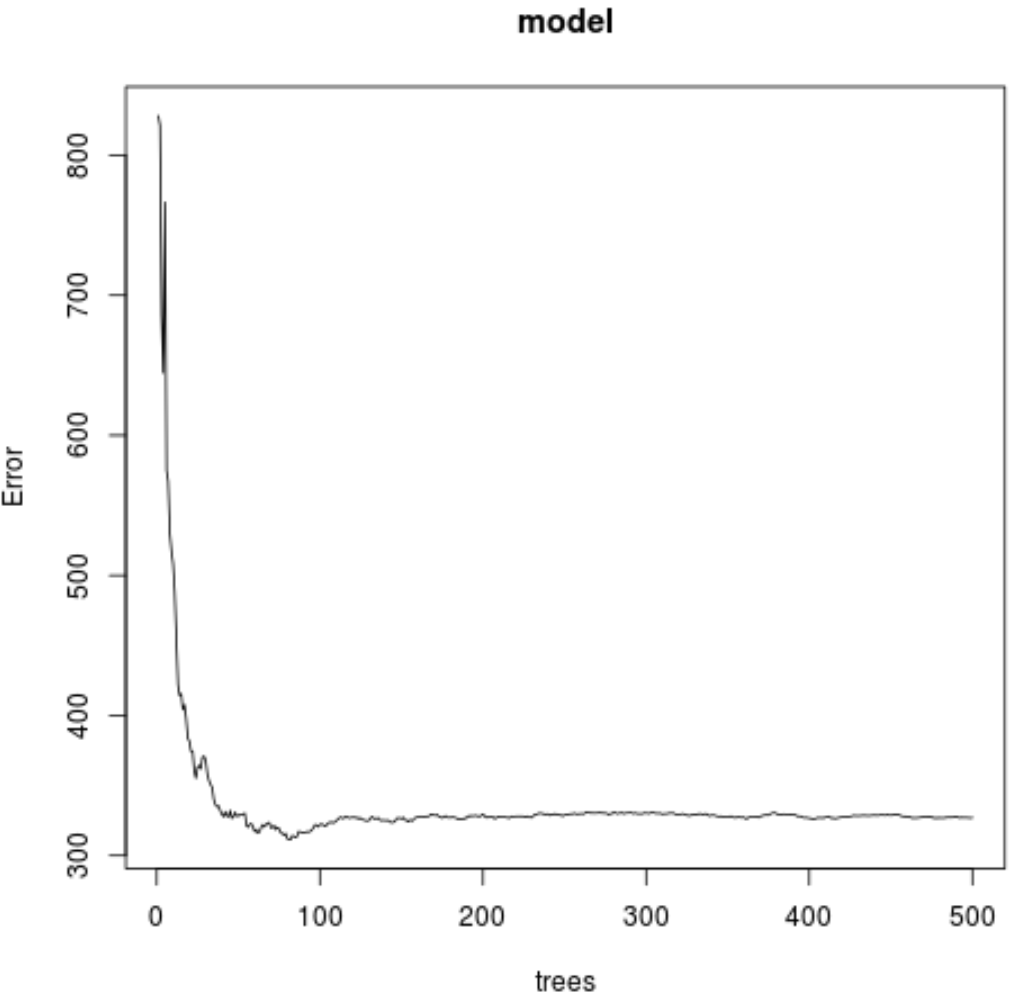
Und wir können die Funktion varImpPlot() verwenden, um ein Diagramm zu erstellen, das die Bedeutung jeder Prädiktorvariablen im endgültigen Modell anzeigt:

 #produce variable importance plot
varImpPlot(model) 

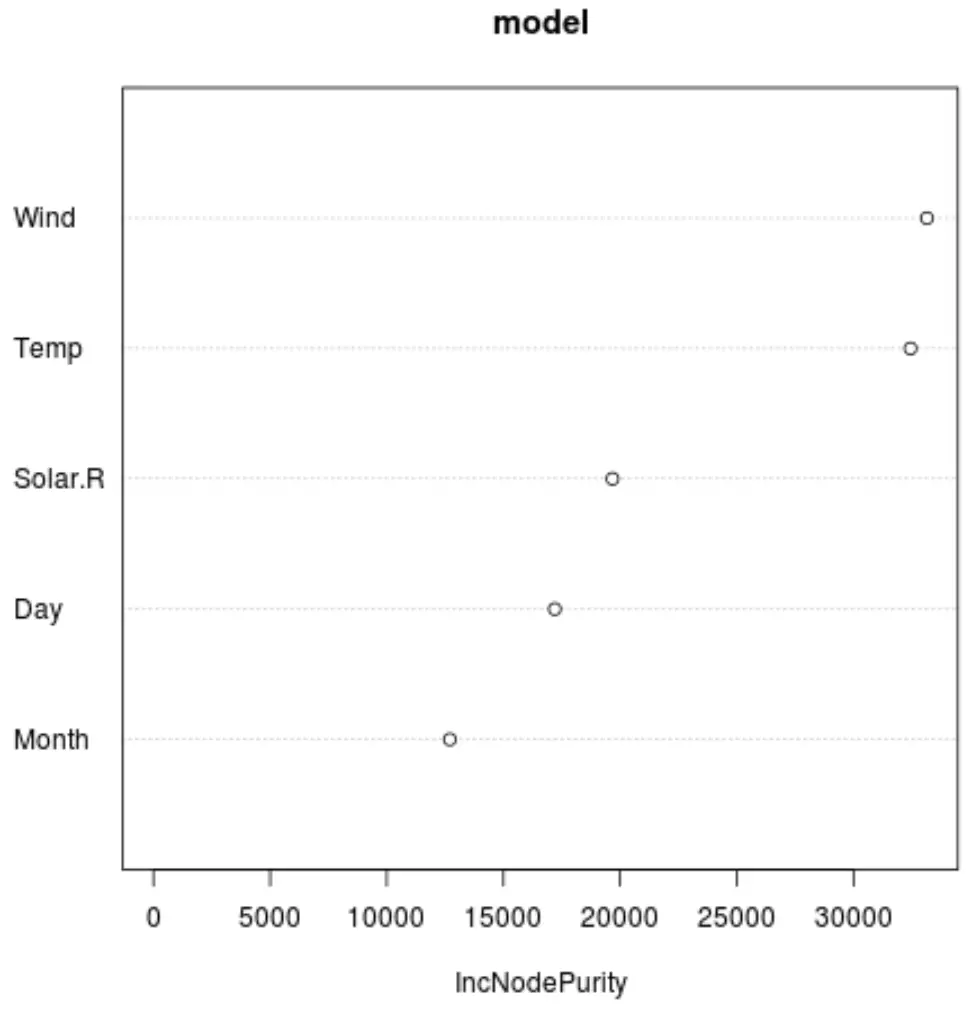
Die x-Achse zeigt die durchschnittliche Zunahme der Knotenreinheit der Regressionsbäume als Funktion der Aufteilung auf die verschiedenen Prädiktoren, die auf der y-Achse angezeigt werden.

Aus der Grafik können wir ersehen, dass Wind die wichtigste Prädiktorvariable ist, dicht gefolgt von Temp .

Schritt 3: Passen Sie das Modell an

Standardmäßig verwendet die Funktion randomForest() 500 Bäume und (Gesamtprädiktoren/3) zufällig ausgewählte Prädiktoren als potenzielle Kandidaten für jede Aufteilung. Wir können diese Parameter mit der Funktion tuneRF() anpassen.

Der folgende Code zeigt, wie Sie anhand der folgenden Spezifikationen das optimale Modell finden:

• ntreeTry: Die Anzahl der zu bauenden Bäume.
• mtryStart: die anfängliche Anzahl der Prädiktorvariablen, die bei jeder Division berücksichtigt werden sollen.
• stepFactor: Faktor, der so lange erhöht wird, bis sich der geschätzte Out-of-Bag-Fehler nicht mehr um einen bestimmten Betrag verbessert.
• verbessern: Der Betrag, um den der Beutelaustrittsfehler verbessert werden muss, um den Schrittfaktor weiter zu erhöhen.

 model_tuned <- tuneRF(
               x=airquality[,-1], #define predictor variables
               y=airquality$Ozone, #define response variable
               ntreeTry= 500 ,
               mtryStart= 4 , 
               stepFactor= 1.5 ,
               improve= 0.01 ,
               trace= FALSE #don't show real-time progress
               )

Diese Funktion erzeugt das folgende Diagramm, das auf der x-Achse die Anzahl der Prädiktoren anzeigt, die bei jeder Teilung beim Erstellen der Bäume verwendet werden, und auf der y-Achse den geschätzten Out-of-Bag-Fehler:

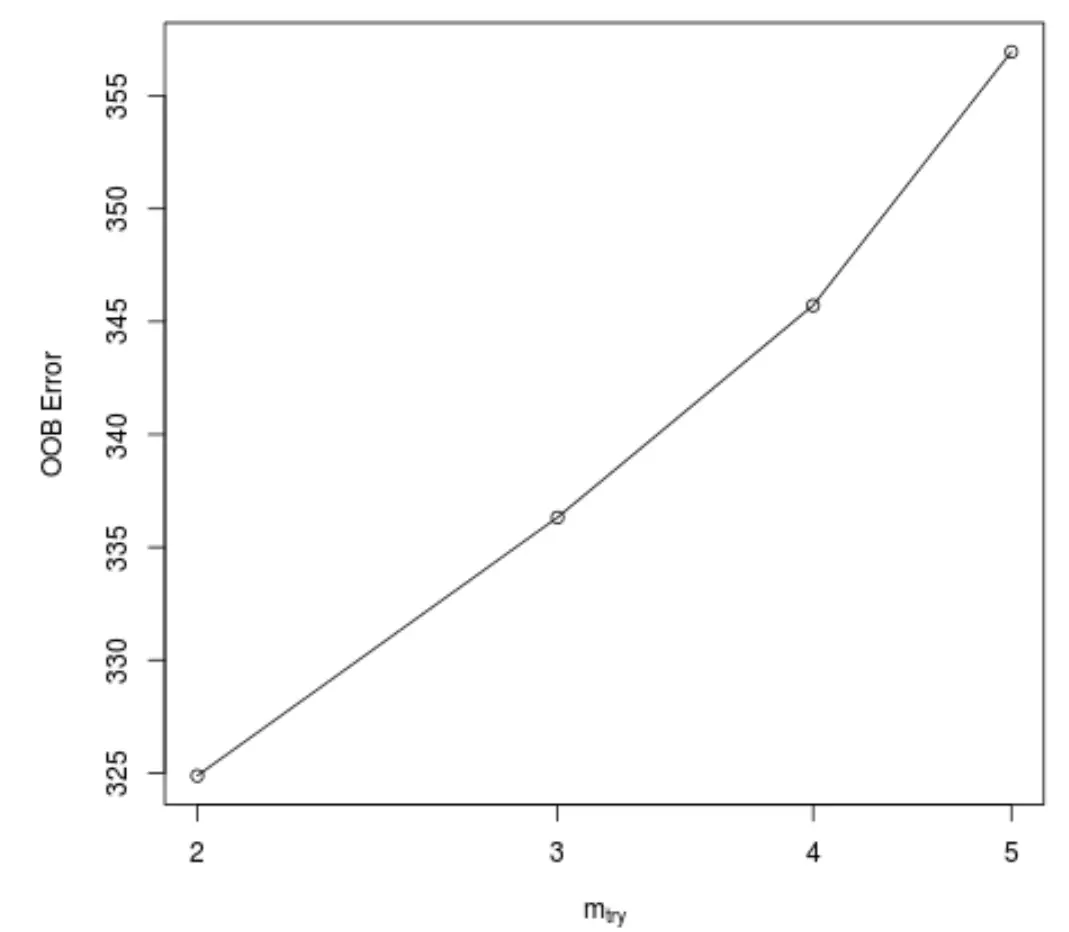
Wir können sehen, dass der niedrigste OOB-Fehler erzielt wird, wenn beim Erstellen der Bäume bei jeder Teilung zwei zufällig ausgewählte Prädiktoren verwendet werden.

Dies entspricht tatsächlich der Standardeinstellung (Gesamtprädiktoren/3 = 6/3 = 2), die von der anfänglichen Funktion randomForest() verwendet wird.

Schritt 4: Verwenden Sie das endgültige Modell, um Vorhersagen zu treffen

Schließlich können wir das angepasste Random-Forest-Modell verwenden, um Vorhersagen über neue Beobachtungen zu treffen.

 #define new observation
new <- data.frame(Solar.R=150, Wind=8, Temp=70, Month=5, Day=5)

#use fitted bagged model to predict Ozone value of new observation
predict(model, newdata=new)

27.19442

Basierend auf den Werten der Prädiktorvariablen sagt das angepasste Zufallswaldmodell voraus, dass der Ozonwert an diesem bestimmten Tag 27,19442 betragen wird.

Den vollständigen R-Code, der in diesem Beispiel verwendet wird, finden Sie hier .