Partielle kleinste quadrate in python (schritt für schritt)

Eines der häufigsten Probleme beim maschinellen Lernen ist die Multikollinearität . Dies tritt auf, wenn zwei oder mehr Prädiktorvariablen in einem Datensatz stark korrelieren.

Wenn dies geschieht, kann ein Modell möglicherweise gut an einen Trainingsdatensatz angepasst werden, bei einem neuen Datensatz, den es noch nie gesehen hat, kann es jedoch eine schlechte Leistung erbringen, da es zu stark an den Trainingsdatensatz angepasst ist . Trainingsset.

Eine Möglichkeit, dieses Problem zu umgehen, besteht darin, eine Methode namens „partielle kleinste Quadrate“ zu verwenden, die wie folgt funktioniert:

• Prädiktor- und Antwortvariablen standardisieren.
• Berechnen Sie M lineare Kombinationen (sogenannte „PLS-Komponenten“) der p ursprünglichen Prädiktorvariablen, die eine signifikante Variation sowohl in der Antwortvariablen als auch in den Prädiktorvariablen erklären.
• Verwenden Sie die Methode der kleinsten Quadrate, um ein lineares Regressionsmodell anzupassen, wobei die PLS-Komponenten als Prädiktoren verwendet werden.
• Verwenden Sie die k-fache Kreuzvalidierung, um die optimale Anzahl von PLS-Komponenten zu finden, die im Modell beibehalten werden sollen.

Dieses Tutorial bietet ein schrittweises Beispiel für die Durchführung partieller kleinster Quadrate in Python.

Schritt 1: Importieren Sie die erforderlichen Pakete

Zuerst importieren wir die Pakete, die zur Durchführung der partiellen kleinsten Quadrate in Python erforderlich sind:

 import numpy as np
import pandas as pd
import matplotlib. pyplot as plt
from sklearn. preprocessing import scale 
from sklearn import model_selection
from sklearn. model_selection import RepeatedKFold
from sklearn. model_selection import train_test_split
from sklearn. cross_decomposition import PLSRegression
from sklearn . metrics import mean_squared_error

Schritt 2: Daten laden

Für dieses Beispiel verwenden wir einen Datensatz namens mtcars , der Informationen zu 33 verschiedenen Autos enthält. Wir werden hp als Antwortvariable und die folgenden Variablen als Prädiktoren verwenden:

• mpg
• Anzeige
• Scheisse
• Gewicht
• qsec

Der folgende Code zeigt, wie dieser Datensatz geladen und angezeigt wird:

 #define URL where data is located
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/mtcars.csv"

#read in data
data_full = pd. read_csv (url)

#select subset of data
data = data_full[["mpg", "disp", "drat", "wt", "qsec", "hp"]]

#view first six rows of data
data[0:6]


        mpg disp drat wt qsec hp
0 21.0 160.0 3.90 2.620 16.46 110
1 21.0 160.0 3.90 2.875 17.02 110
2 22.8 108.0 3.85 2.320 18.61 93
3 21.4 258.0 3.08 3.215 19.44 110
4 18.7 360.0 3.15 3.440 17.02 175
5 18.1 225.0 2.76 3.460 20.22 105

Schritt 3: Passen Sie das Modell der partiellen kleinsten Quadrate an

Der folgende Code zeigt, wie das PLS-Modell an diese Daten angepasst wird.

Beachten Sie, dass cv = RepeatedKFold() Python anweist, die k-fache Kreuzvalidierung zu verwenden, um die Modellleistung zu bewerten. Für dieses Beispiel wählen wir k = 10 Falten, dreimal wiederholt.

 #define predictor and response variables
X = data[["mpg", "disp", "drat", "wt", "qsec"]]
y = data[["hp"]]

#define cross-validation method
cv = RepeatedKFold(n_splits= 10 , n_repeats= 3 , random_state= 1 )

mse = []
n = len (X)

# Calculate MSE with only the intercept
score = -1*model_selection. cross_val_score (PLSRegression(n_components=1),
n.p. ones ((n,1)), y, cv=cv, scoring=' neg_mean_squared_error '). mean ()    
mse. append (score)

# Calculate MSE using cross-validation, adding one component at a time
for i in np. arange (1, 6):
    pls = PLSRegression(n_components=i)
    score = -1*model_selection. cross_val_score (pls, scale(X), y, cv=cv,
               scoring=' neg_mean_squared_error '). mean ()
    mse. append (score)

#plot test MSE vs. number of components
plt. plot (mse)
plt. xlabel (' Number of PLS Components ')
plt. ylabel (' MSE ')
plt. title (' hp ')

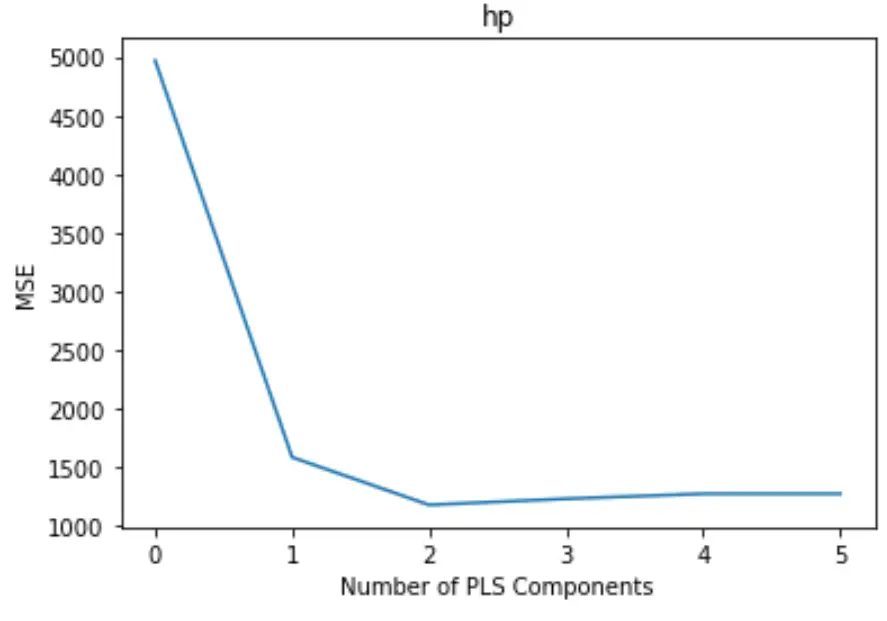
Das Diagramm zeigt die Anzahl der PLS-Komponenten entlang der x-Achse und den MSE-Test (mittlerer quadratischer Fehler) entlang der y-Achse.

Aus der Grafik können wir ersehen, dass der MSE des Tests durch das Hinzufügen von zwei PLS-Komponenten abnimmt, aber zu steigen beginnt, wenn wir mehr als zwei PLS-Komponenten hinzufügen.

Somit umfasst das optimale Modell nur die ersten beiden PLS-Komponenten.

Schritt 4: Verwenden Sie das endgültige Modell, um Vorhersagen zu treffen

Wir können das endgültige PLS-Modell mit zwei PLS-Komponenten verwenden, um Vorhersagen über neue Beobachtungen zu treffen.

Der folgende Code zeigt, wie man den Originaldatensatz in einen Trainings- und einen Testsatz aufteilt und das PLS-Modell mit zwei PLS-Komponenten verwendet, um Vorhersagen für den Testsatz zu treffen.

 #split the dataset into training (70%) and testing (30%) sets
X_train , _

#calculate RMSE
pls = PLSRegression(n_components=2)
pls. fit (scale(X_train), y_train)

n.p. sqrt (mean_squared_error(y_test, pls. predict (scale(X_test))))

29.9094

Wir sehen, dass der RMSE des Tests 29,9094 beträgt. Dies ist die durchschnittliche Abweichung zwischen dem vorhergesagten HP- Wert und dem beobachteten HP- Wert für die Testsatzbeobachtungen.

Den vollständigen in diesem Beispiel verwendeten Python-Code finden Sie hier .