So führen sie einen t-test bei zwei stichproben in excel durch

Ein T-Test mit zwei Stichproben wird verwendet, um zu testen, ob die Mittelwerte zweier Grundgesamtheiten gleich sind oder nicht.

In diesem Tutorial wird erläutert, wie Sie einen T-Test bei zwei Stichproben in Excel durchführen.

So führen Sie einen T-Test bei zwei Stichproben in Excel durch

Angenommen, Forscher möchten wissen, ob zwei verschiedene Pflanzenarten in einem bestimmten Land die gleiche durchschnittliche Höhe haben. Da es zu lange dauern würde, jede einzelne Pflanze zu vermessen, beschlossen sie, eine Probe von 20 Pflanzen jeder Art zu entnehmen.

Das folgende Bild zeigt die Höhe (in Zoll) jeder Pflanze in jeder Probe:

Wir können einen T-Test mit zwei Stichproben durchführen, um zu bestimmen, ob die beiden Arten die gleiche durchschnittliche Größe haben, indem wir die folgenden Schritte ausführen:

Schritt 1: Bestimmen Sie, ob die Populationsvarianzen gleich sind .

Wenn wir einen t-Test bei zwei Stichproben durchführen, müssen wir zunächst entscheiden, ob wir davon ausgehen, dass die beiden Grundgesamtheiten gleiche oder ungleiche Varianzen aufweisen. Im Allgemeinen können wir davon ausgehen, dass Populationen gleiche Varianzen aufweisen, wenn das Verhältnis der größten Stichprobenvarianz zur kleinsten Stichprobenvarianz weniger als 4:1 beträgt.

Wir können die Varianz für jede Stichprobe mithilfe der Excel-Funktion =VAR.S(Cell range) ermitteln, wie in der folgenden Abbildung dargestellt:

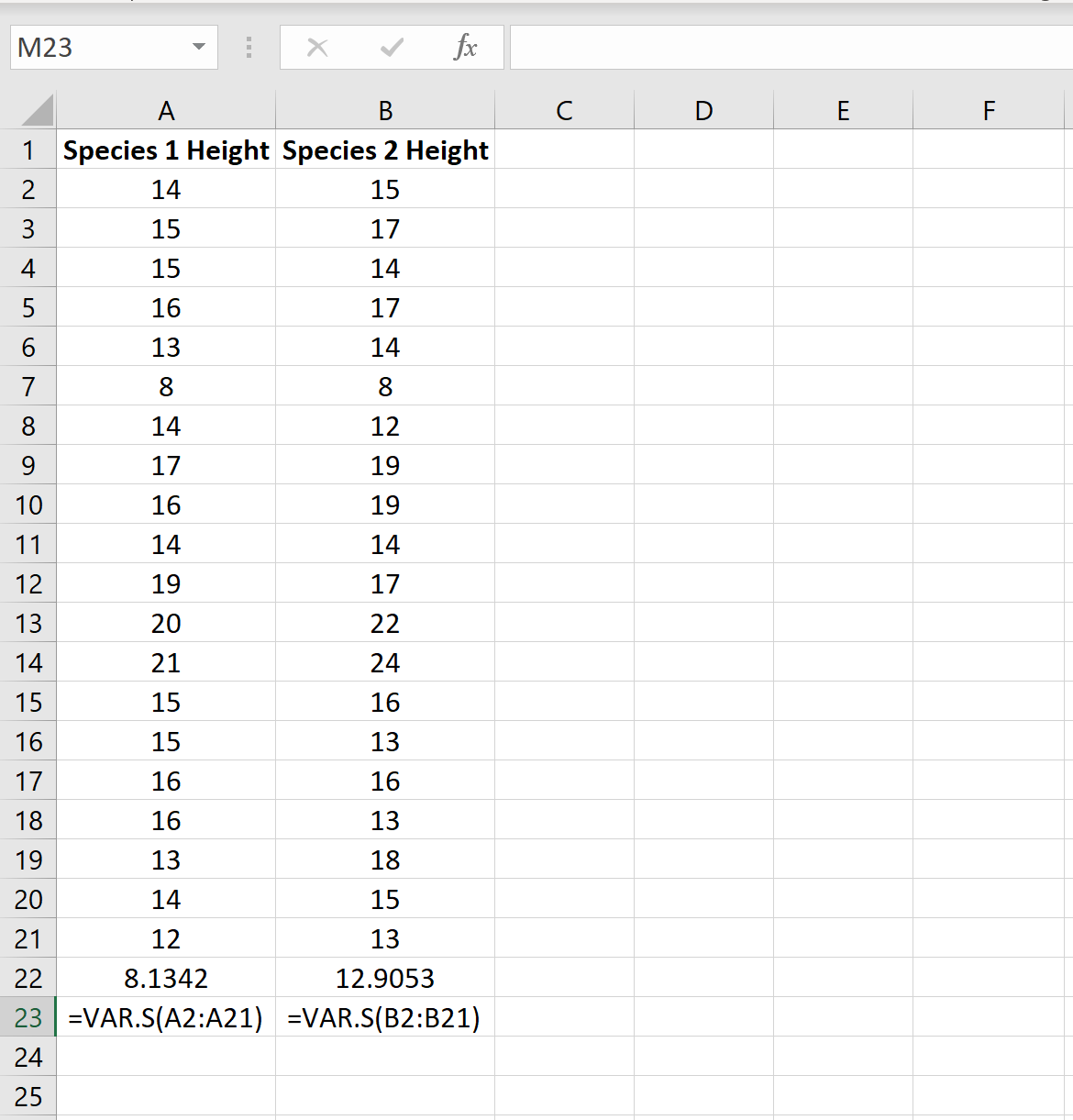
Das Verhältnis der größten Stichprobenvarianz zur kleinsten Stichprobenvarianz beträgt 12,9053/8,1342 = 1,586 , was weniger als 4 ist. Das bedeutet, dass wir davon ausgehen können, dass die Populationsvarianzen gleich sind.

Schritt 2: Öffnen Sie das Analysis ToolPak .

Klicken Sie im oberen Menüband auf der Registerkarte „Daten“ auf „Datenanalyse“.

Wenn Sie diese Option zum Klicken nicht sehen, müssen Sie zunächst das Analysis ToolPak herunterladen , das völlig kostenlos ist.

Schritt 3: Wählen Sie den entsprechenden Test aus.

Wählen Sie die Option „ t-test: zwei Stichproben unter der Annahme gleicher Varianzen“ aus und klicken Sie dann auf „OK“.

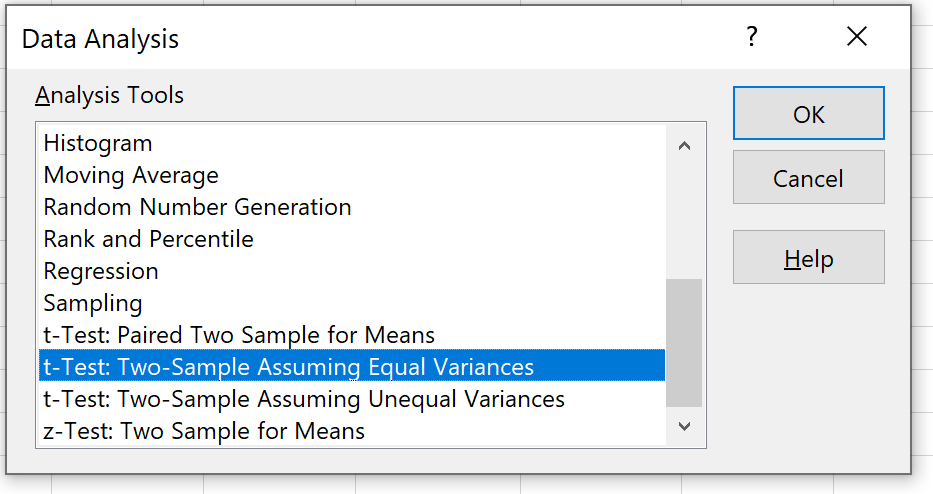
Schritt 4: Geben Sie die erforderlichen Informationen ein .

Geben Sie den Wertebereich für Variable 1 (unsere erste Stichprobe), Variable 2 (unsere zweite Stichprobe) und die hypothetische mittlere Differenz ein (in diesem Fall geben wir „0“ ein, weil wir wissen möchten, ob die wahre mittlere Differenz der Grundgesamtheit 0 ist). und den Ausgabebereich, in dem die T-Test-Ergebnisse angezeigt werden sollen. Klicken Sie dann auf OK.

Schritt 5: Interpretieren Sie die Ergebnisse .

Sobald Sie im vorherigen Schritt auf OK geklickt haben, werden die T-Test-Ergebnisse angezeigt.

So interpretieren Sie die Ergebnisse:

Durchschnitt: Dies ist der Durchschnitt jeder Stichprobe. Probe 1 hat eine durchschnittliche Höhe von 15,15 und Probe 2 hat eine durchschnittliche Höhe von 15,8 .

Varianz: Dies ist die Varianz für jede Stichprobe. Stichprobe 1 hat eine Varianz von 8,13 und Stichprobe 2 hat eine Varianz von 12,90 .

Beobachtungen: Dies ist die Anzahl der Beobachtungen in jeder Stichprobe. Beide Proben enthalten 20 Beobachtungen (z. B. 20 einzelne Pflanzen in jeder Probe).

Gepoolte Varianz: Zahl, die durch „Pooling“ der Varianzen jeder Stichprobe mithilfe der Formel s ² _p = [ (n ₁ -1)s ² ₁ + (n ₂ -1)s ² ₂ ] / (n ₁ +n ₂ -) berechnet wird. 2), was sich als 10,51974 herausstellt. Diese Zahl wird dann bei der Berechnung der t -Test-Statistik verwendet.

Hypothetische Mittelwertdifferenz: Die Zahl, über die wir Hypothesen aufstellen, ist die Differenz zwischen den Mittelwerten der beiden Grundgesamtheiten. In diesem Fall haben wir 0 gewählt, weil wir testen möchten, ob die Differenz zwischen den Mittelwerten der beiden Grundgesamtheiten gleich 0 ist, beispielsweise wenn kein Unterschied besteht.

df: Die Freiheitsgrade für den t-Test, berechnet als n ₁ + n ₂ -2 = 20 + 20 – 2 = 38 .

t Stat: Die Teststatistik t , berechnet als t = [ x ₁ – x ₂ ] / √ [s ² _p (1/n ₁ + 1/n ₂ )]

In diesem Fall ist t = [15,15-15,8] / √ [10,51974(1/20+1/20)] = -0,63374 .

Zweiseitiger P(T<=t): der p-Wert für einen zweiseitigen t-Test. In diesem Fall ist p = 0,530047 . Dies ist viel größer als Alpha = 0,05, sodass wir die Nullhypothese nicht ablehnen können. Wir haben keine ausreichenden Beweise dafür, dass die Mittelwerte der beiden Populationen unterschiedlich sind.

t Zweiseitiger kritischer Wert: Dies ist der kritische Wert des Tests, der durch Identifizieren des Werts in der t-Verteilungstabelle ermittelt wird, der einem zweiseitigen Test mit Alpha = 0,05 und df = 38 entspricht. Dies ergibt 2. 024394 . Da unsere t- Test-Statistik unter diesem Wert liegt, können wir die Nullhypothese nicht ablehnen. Wir haben keine ausreichenden Beweise dafür, dass die Mittelwerte der beiden Populationen unterschiedlich sind.

Beachten Sie, dass der p-Wert- und der kritische Wertansatz beide zu derselben Schlussfolgerung führen.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere Arten von T-Tests in Excel durchführen:

So führen Sie einen T-Test bei einer Stichprobe in Excel durch
So führen Sie einen T-Test für gepaarte Stichproben in Excel durch